5.10. Потенциальная энергия упругой деформации
Как было выяснено ранее, удельная потенциальная энергия упругой деформации определяется формулой
.
Рассмотрим случай чистого изгиба (M = const, Q = 0).
Имеет место линейное напряжённое состояние:
,
σ2
= 0, σ3
= 0.
Найдем потенциальную энергию в элементарном объёме dV балки:
.
Если учесть, что ε1 = σ1/Е, то получим
.
Подставим сюда значение напряжения σ1, а затем проинтегрируем по всему объёму балки:
.
Для выполнения интегрирования учтём, что
dV = dx ∙ dF.
Переходя к двум переменным, необходимо интеграл по объёму заменить двойным интегралом:
. (5.52)
Учтём при этом, что
. (а)
Подставляя значение (а) в выражение (5.52), окончательно получим
. (5.53)
Заметим, что в формулу (5.53) изгибающий момент входит в квадрате и поэтому величина потенциальной энергии всегда положительная.
Для балок, работающих при поперечном изгибе (Q 0, M = M(x)), потенциальная энергия сдвига (от действия касательных напряжений) как правило, на порядок и более меньше потенциальной энергии изгиба. Поэтому формулу (5.53), выведенную для случая чистого изгиба, распространяют и на случай поперечного изгиба, когда М = М(х):
. (5.54)
Глава 6. Сдвиг
Напряжения и деформации при чистом сдвиге
Чистым сдвигом называется такой частный случай плоского напряжённого состояния, при котором на площадках бесконечно малого элемента действуют только касательные напряжения (рис.6.1).
Рис. 6.1
Чистый сдвиг имеет место при работе ряда элементов конструкций. Так, мы встречались с этим напряжённым состоянием, когда рассчитывали на прочность балки при поперечном изгибе, – на нейтральной линии σ = 0 и τ = τmax (см. п.5.8). Кроме того, в условиях чистого сдвига находится материал при резке ножницами (рис.6.2,а), при кручении круглого сплошного или трубчатого стержня (рис.6,2б), в заклёпочных (рис.6.2,в), болтовых и сварных соединениях.
а б в
Рис. 6.2
Определим напряжения по наклонным площадкам (рис.6.3). По формулам (3.9) и (3.10) при плоском напряжённом состоянии
σα = σxcos2α + τσysin2α – τxysin 2α,
.
В нашем случае σx = σy = 0, τxy = τ поэтому получим
σα = – τ sin 2α, (6.1)
τα = τ cos 2α. (6.2)
При α = ± 450 τα = 0 и σα = τ, т.е. главные напряжения при чистом сдвиге (рис.6.3)
. (6.3)
Итак, главные напряжения – сжимающее и растягивающее – равны между собой и численно равны экстремальным касательным напряжениям.
Рис.6.3
Тот же самый результат можно получить, используя формулу (3.18) для определения главных напряжений при плоском напряжённом состоянии
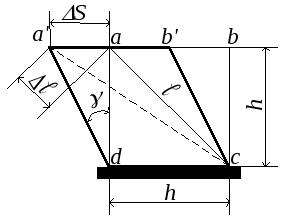
Рассмотрим деформацию элемента abcd (рис.6.4). Закрепляем одну из граней. Квадрат abcd превращается в ромб abcd, поскольку по граням элемента нет нормальных напряжений. В то же время диагональ ac, совпадающая с направлением σ1, удлиняется, а диагональ bd – укорачивается.
|
Рис.6.4 |
∆S – абсолютный сдвиг (смещение грани ab); γ – угол сдвига или относительный сдвиг. |
. (6.4)
ac
= ℓ – длина диагонали,
,
∆ℓ – абсолютное удлинение диагонали,
∆ℓ = a′a ∙ cos 450 = ∆S ∙ cos 450 = γh ∙ cos 450. Относительное удлинение диагонали есть не что иное, как главное удлинение ε1 при плоском напряжённом состоянии, поскольку главное напряжение σ1 действует в направлении диагонали ac.
.
Итак, при чистом сдвиге
. (6.5)
Теперь выразим ε1 через σ, воспользовавшись обобщённым законом Гука для плоского напряжённого состояния (3.26)
. (6.6)
Приравняем правые части формул (6.5) и (6.6)
,
.
Множитель перед γ является коэффициентом пропорциональности между касательным напряжением и соответствием ему углом сдвига, и называется модулем сдвига или модулем касательной упругости:
. (6.7)
Для стали G = 8 ∙103 кН/см2 или G = 8 ∙ 104 МПа.
Модуль сдвига – это третья упругая постоянная изотропного упругого материала, выражающаяся через первые две (модуль нормальной упругости Е и коэффициент Пуассона ν) формулой (6.7).
Таким образом, закон Гука при сдвиге имеет вид
τ = Gγ. (6.8)
В аналогичной форме записывается этот фундаментальный закон и при линейном напряжённом состоянии – σ = Eε (см. формулу (2.9)), и при объёмном напряжённом состоянии: σcp = Kθ (см. формулу (3.36)).