TVIMS2

-(1 0,2)5

# -(1 0,2)4 0,2

2.1.87. (НТ3). Случайная величина X - число бросаний монеты до первого появления орла. Чему равна вероятность события M {X 2}:

-0,

#- 1 4

-1

2

2.1.88. (НТ1). Вероятность брака партии изделий равна p 0,02. Сколько в среднем будет бракованных деталей в партии, содержащей 1000 деталей

#-20

-50 - 100

2.1.89. (НТ3). Радист вызывает корреспондента до тех пор, пока вызов не будет

принят. Вероятность того, что корреспондент примет вызов, равна 1 . Каков закон

4

распределения с.в. X -числа вызовов:

-

		1			3			9
		4		16			64

-

1 3

416

#-

	1			2			3	4	…
		1			1
	4			16					…

2.1.91. (НТ3). Случайная величина X распределена по геометрическому закону. Какова вероятность A {X m}:

-1 p m 1 ,

#- qm ,

-qm p?

2.1.92. (НТ1). Какой формулой определяется биномиальное распределение?

#- P(X m) Cnm pmqn m

-P(X m) Cnm pnqn m

-P(X m) Cnm pnqn

2.1.93. (НТ1). Случайная величина Х распределена по биномиальному закону.

Х - это:

а) непрерывная случайная величина

#б) дискретная случайная величина в) смешанная случайная величина

2.1.94. (НТ1). Случайная величина X имеет биномиальное распределение.

X -это:
# - вероятность m успехов в серии	n независимых испытаний с
вероятностью успеха p в единичном опыте,
- вероятность n успехов в серии	mнезависимых испытаний с
вероятностью успеха p в единичном опыте,

- вероятность того, что в n испытаниях успех произойдет в m -ом опыте 2.1.95. (НТ1). В биномиальном распределении случайной величины X ,

P(X m) Cnm pmqn m , величина m принимает значения:

--1,0,1,… n

-0,1,2,… n

#- 1,2,3,… n

2.1.96. (НТ1). Что означает величина p при биномиальном распределении P(X m) Cnm pmqn m случайной величины X ?

- вероятность появления одного успеха в серии из n независимых

испытаний

- вероятность появления успеха во всех независимых испытаниях

#-вероятность появления успеха в каждом независимом испытании ? 2.1.97. (НТ1). Что означает величина p при биномиальном распределении

P(X m) Cnm pmqn m случайной величины X ?

- вероятность появления одной неудачи в серии из n независимых

испытаний

- вероятность появления неудачи во всех независимых испытаниях

#-вероятность появления неудачи в каждом n независимом из испытании 2.1.98. (НТ1). Чему равно математическое ожидание случайной величины X ,

распределенной по биномиальному закону:

# -D[X] np

-D[X] npq

-D[X] 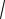npq ?

2.1.99. (НТ1). Чему равна дисперсия случайной величины X , распределенной по биномиальному закону7

-D[X] np

# - D[X] npq

- D[X] npq ?

2.1.100. (НТ1). Чему равно среднее квадратическое отклонение случайной величины X , распределенной по биномиальному закону7

-D[X] np

-D[X] npq

# - D[X] 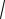npq ?

2.1.101. (НТ1). Производится пять выстрелов по мишени с вероятностью попадания в одном выстреле p 0,6. Какие значения принимает случайная величина X - число попаданий по мишени:

-1; 2; 3; 4; 5

#- 0; 1; 2; 3; 4; 5

-2; 3; 4; 5

2.1.102. (НТ1). Производится пять выстрелов по мишени с вероятностью попадания в одном выстреле p 0,6. Чему равно математическое ожидание случайной величины X - число попаданий по мишени?

-2

#- 3

-10

2.1.103. (НТ2). Производится пять выстрелов по мишени с вероятностью попадания в одном выстреле p 0,6. Чему равна дисперсия случайной величины X - число попаданий по мишени:

#- 1,2

-2,4

-3,6

2.1.104. (НТ1). Производится пять выстрелов по мишени с вероятностью попадания в одном выстреле p 0,6. Чему равно среднее квадратическое отклонение случайной величины X - число попаданий по мишени:

# - 1,2

-2,4

-3,6

2.1.105. (НТ3). В каких случаях формула ПуассонаP (m) me ( np)

n

n!

используется в качестве приближения для формулы Бернулли?

#- когда n- велико, p - мало

-когда n- велико, p - велико

-когда n- мало, p - мало

2.1.106. (НТ1). Для какой схемы распределение Пуассона используется в качестве приближения?

-схемы до первого успеха

#- схемы Бернулли

-полной группы несовместных событий

2.1.107. (НТ2). Какие значения принимает величина m в законе Пуассона

Pn (m) me ? n!

#- 0; 1; 2; 3;……………

-1; 2; 3;……………

-0

2.1.108. (НТ2). Чему равно математическое ожидание случайной величины X , распределенной по закону Пуассона?

# -D[X]

-D[X] 2

-D[X]

2.1.109. (НТ1). Чему равна дисперсия случайной величины X , распределенной по биномиальному закону?

-D[X]

#- D[X] 2

- D[X]

2.1.110. (НТ1). Чему равно среднее квадратическое отклонение случайной величины X , распределенной по закону Пуассона?

-D[X]

-D[X] 2

#- D[X]

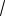
2.2.1.(НТ1). Какие значения может принимать непрерывная случайная

величина?

- конечный набор значений -счетный набор значений

#-любое значение из интервала, конечного или бесконечного 2.2.2.(НТ1). Каким свойством обладает плотность распределения вероятностей

f (x)?

-f (x) 0

#- f (x) 0

-f (x) 0

2.2.3.(НТ1). Что является нормирующим свойством для плотности вероятностей

f (x)?

- f (x)dx 0

#- f (x)dx 1

- f (x)dx

2.2.4.(НТ1). Как определяется функция распределения F(x) для непрерывной случайной величины?

-F(x) P[X x]

#-F(x) P[X x]

-F(x) P[X x]

2.2.5.(НТ1). Как по плотности распределения f (x) вычислить функцию распределения F(x)?

x

- F(x) f (t)dt

0

x

#-F(x) f (t)dt

-F(x) f (t)dt

2.2.6.(НТ1). Как по функции распределения F(x) вычислить плотность распределения f (x)?

- f (x) F' (x)

- f (x) F(x)dx

#- f (x) F'(x)

2.2.7.(НТ1). Функция f (x) позволяет вычислить вероятность попадания непрерывной случайной величины в произвольный интервал (x1; x2 ) как:

x2

#- P(x1 X x2 ) f (x)dx

x1

x1

-P(x1 X x2) f (x)dx

x2

P(x1 X x2 ) f (x)dx

2.2.8.(НТ1). Функция F(x) непрерывной случайной величины удовлетворяет следующему свойству:

- F(x) – постоянная функция

#- F(x) – неубывающая функция F(x) – возрастающая функция

2.2.9.(НТ1). Функция F(x) непрерывной случайной величины удовлетворяет следующему свойству:

- lim F(x) 1

x

#- lim F(x) 0

-lim F(x)

x

2.2.10.(НТ1). Функция F(x) непрерывной случайной величины удовлетворяет следующему свойству:

- lim F(x) 0

x

#- lim F(x) 1

-lim F(x)

x

2.2.11.(НТ1). Пользуясь функцией распределения F(x)можно вычислить вероятность попадания непрерывной случайной величины в произвольный интервал

(x1; x2 ) как:

#- P[x1 X x2] F(x2) F(x1) - P[x1 X x2 ] F(x1) F(x2 )

- P[x1 X x2 ] 0

2.2.12.(НТ1). Математическое ожидание непрерывной случайной величины можно вычислить как:

#- M[X] xf (x)dx

- M[X] x2 f (x)dx

- M[X] f (x)dx

2.1.13. (НТ1). Математическое ожидание постоянной величины C равно:

-M[C] 1

-M[C] 0

#- M[C] C

2.1.14. (НТ1). Для математического ожидания непрерывной случайной величины справедлива формула ( X -случайная величина,C - произвольная константа):

-M[CX] M[X]

# - M[CX] CM[X]

-M[CX] C2M[X]

2.1.15. (НТ1). Для двух произвольных непрерывных случайных величин X и Y справедливо следующее равенство:

#- M[X Y] M[X] M[Y]

-M[X Y] M[X] M[Y]

-M[X Y] 0

2.1.16. (НТ1). Для двух произвольных непрерывных случайных величин X и

Yсправедливо следующее равенство:

-M[X Y] M[X] M[Y]

#- M[X Y] M[X] M[Y]

-M[X Y] 0

2.1.17. (НТ1). Для двух непрерывных случайных величин случайных величин X и Y справедливо следующее равенство M[X Y] M[X] M[Y] если:

-случайные величины X и Y зависимы

#- случайные величины X и Y независимы

-случайные величины X и Y несовместны

2.1.18. (НТ1). Для произвольной непрерывной случайной величины X дисперсию можно вычислить по формуле:

#- D[X] (x M[X])2 f (x)dx

#- D[X] M[X2] (M[X])2

-D[X] (x M[X])f (x)dx

2.1.19. (НТ1). При умножении непрерывной случайной величины X на константу C выполняется следующая формула:

#- D[CX] C2D[X]

-D[CX] CD[X]

-D[CX] D[X]

2.1.20. (НТ1). Среднее квадратическое отклонение непрерывной случайной величины вычисляется по следующей формуле:

-[X] D[X] 2

#- [X] 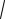D[X]

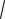-[X] 4D[X]

2.1.21. (НТ2). Непрерывная случайная величина X измеряется в метрах. В каких единицах измеряется плотность распределения вероятностей f (x)?

-ì

-ì 2

#- 1

ì

2.1.22. (НТ2). Непрерывная случайная величина X измеряется в метрах. В каких единицах измеряется функция распределения F(x)?

- ì

#-безразмерная

-1

ì

2.1.23. (НТ2). Непрерывная случайная величина X измеряется в метрах. В каких единицах измеряется ее математическое ожидание M[X]?

#- ì -безразмерная

- ì 2

2.1.24. (НТ2). Непрерывная случайная величина X измеряется в метрах. В каких единицах измеряется ее дисперсия D[X]?

- ì -безразмерная

#- ì 2

2.1.25. (НТ2). Непрерывная случайная величина X измеряется в метрах. В каких единицах измеряется ее среднее квадратическое отклонение [X]?

#- ì -безразмерная

- ì 2

2.1.26. (НТ1). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна плотность распределения f (x)на этом интервале?

#- 1 b a

-1 a b

-0

2.1.27. (НТ1). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна плотность распределения f (x) вне этого интервала?

-1 b a

-1 a b

#- 0

2.1.28. (НТ2). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна функция распределения F(x) на этом интервале?

#- x a b a

-x b a b

-1

2.1.29. (НТ2). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна функция распределения F(x) правее этого интервала?

-x a b a

-0

#-1

2.1.30. (НТ2). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна функция распределения F(x) левее этого интервала?

-x a b a

-x b a b

#-0

2.1.31. (НТ1). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равно математическое ожидание этой случайной величины?

#- a b 2

-a b

2

-a b 2

12

2.1.32. (НТ2). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равна дисперсия этой случайной величины?

#- a b 2

-a b

2

#- a b 2 12

2.1.33. (НТ1). Случайная величина X имеет равномерное распределение на интервале (a;b). Чему равно среднее квадратическое отклонение этой случайной величины?

- b a

2

- a b

2

# -

b a

2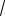3

2.2.34.(НТ1). Случайная величина распределена равномерно на интервале

( a; a).

Чему равна плотность распределения вероятностей на этом интервале?

#- 1 a

-1

2a

-1

4a

2.2.35.(НТ1). Случайная величина распределена равномерно на интервале

( 1; 4).

Чему равна плотность распределения вероятностей на этом интервале?

#- 1 5

-1

4

-1

6

2.2.36.(НТ1). Данное распределение случайной величины

	1		при х 1; 4
				является:
		5
	f (x)		при х 1;
	0			4 .

-пуассоновским

-релеевским

#- равномерным

2.2.37.(НТ1). Математическое ожидание непрерывной случайной величины с

плотностью распределения
				1					х 1; 4
						при
				f (x) 5						равно:
				0		при			х 1; 4 .
-	5
2
#-		3
2
-0
2.2.38.(НТ1). Дисперсия						непрерывной случайной величины с законом
плотности распределения f(x)
						1			при	х 1; 4
				f (x) 5						равна:
						0			при	х 1; 4 .

#-25/12 -5/12 -5/2

2.2.39.(НТ1). Случайная величина Х задана плотностью распределения f(x)

1		при	х 1; 4
f (x) 5			х 1; 4 .
0		при

Вероятность того, что х < 3 равна: -3/5 -3/4

#-4/5

2.2.40.(НТ1). Случайная величина Х задана плотностью распределения f(x)

1			при	х 1; 4
f (x) 5				х 1; 4 .
0			при
Вероятность того, что –1 < х < 1			равна:
#-2/5

-1/5 -1/2

2.2.41.(НТ1). Случайная величина Х задана плотностью распределения f(x)

1		при	х 1; 4
f (x) 5			х 1; 4 .
0		при

Вероятность того, что 3< x < 4 равна: -2/5

#-1/5 -1/2

2.2.42.(НТ1). Случайная величина Х распределена равномерно на интервале

(1; a 1).

Чему равна плотность распределения вероятностей на этом интервале? -1 -0

#- 1 a

2.2.43.(НТ2). Случайная величина Х распределена равномерно на интервале

(1; a 1).

Чему равна функция распределения на этом интервале?

#- x 1 a 2

-x 2 a 1

-x 2 12

2.2.44.(НТ2). Случайная величина Х распределена равномерно на интервале

(1; a 1).

Чему равна функция распределения правее этого интервала?

#-1 -0

-x 2 a 1