TVIMS2

2.2.45.(НТ2). Случайная величина Х распределена равномерно на интервале

(1; a 1).

Чему равна функция распределения левее этого интервала? -1

#-0

-x 2 a 1

2.1.46. (НТ1). Данное распределение случайной величины

		1	ïðè	õ 1; à 1
					является:
		à
	f (x)			õ 1; à 1,
	0 ïðè				à 0.

- пуассоновским -экспоненциальным

#- равномерным 2.2.47.(НТ1). Математическое ожидание непрерывной случайной величины с

плотностью распределения

	1	ïðè	õ 1; à 1
	à
f (x)			õ 1; à 1,
0 ïðè				à 0.

Равно: - а/2

#-(а+2) /2 -(а-2) 2 /12

2.2.48.(НТ1). Дисперсия непрерывной случайной величины с плотностью распределения f(x)

1

ïðè

õ 1; à 1

f (x)

равна:

à

õ 1; à 1,

0

ïðè

à 0.

- а 2 /2

#- а 2 /12

-(а +2)/2

2.2.49.(НТ1). Среднее квадратическое отклонение

непрерывной случайной

величины с плотностью распределения

1

ïðè

õ 1; à 1

f (x)

à

õ 1; à 1,

0

ïðè

à 0.

Равна:

-

a

2

#-

a

2

3

-1

2.2.50.(НТ2). Данная функция

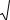
0 при х 2

x 2
F(x)			при х 2; 4
		2
			при х 4
1

является функцией распределения : - нормальной случайной величины

#-равномерной случайной величины - пуассоновской случайной величины

2.2.51.(НТ1). Случайная величина называется распределенной по показательному закону, если ее плотность распределения вероятностей имеет вид:

#- f (x)			0,x 0
	e x,x 0
			2
x				x
					2
			e 2				при х 0
- f (x)
		2
							при х 0
0

		1		е	х а2
- f (x)					2а
		2 а

2.2.52.(НТ2). Случайная величина называется распределенной по показательному закону, если ее плотность распределения вероятностей имеет вид:

0;		x 0
-F(x) 1 e x;		x 0
0;		x 0
-F(x)	x;	x 0
e
0;		x 0
#-F(x) 1 e x ;		x 0

2.1.53. (НТ1). Случайная величина X распределена по показательному

	0,x 0
закону f (x)	. Чему равно математическое ожидание этой случайной

e x,x 0

величины? -1

#- - 2

2.1.54. (НТ1). Случайная величина X распределена по показательному

	0,x 0
закону f (x)	. Чему равна дисперсия этой случайной величины?

e x,x 0

-1 -

#- 2

2.1.55. (НТ1). Случайная величина X распределена по показательному

	0,x 0
закону f (x)	. Чему равно среднее квадратическое отклонение этой

e x,x 0

случайной величины? -1

#
- 2
2.2.56.(НТ1).	Случайная	величина,			имеющая плотность распределения
вероятностей			2х
		е		при	х 0
	f (x) 2
				при	х 0
	0

распределена по: -нормальному закону

#-показательному закону -равномерному закону

2.2.57.(НТ1). Случайная величина, имеющая функцию распределения

0;	x 0
F(x) 1 e 2x;	x 0

распределена по:

#-показательному закону -равномерному закону. -нормальному закону

2.2.58.(НТ1). Математическое ожидание непрерывной случайной величины с законом распределения

		2х
	е		при	х 0равно:
f (x) 2
			при	х 0
0

-1

-1

2

#-2 2.2.59.(НТ1). Дисперсия непрерывной случайной величины с законом

распределения

	2х	при	х 0
2е				равно:
f (x)
		при	х 0
0
-1/2
- 1
4
#-4
2.2.60.(НТ1). Среднее квадратическое			отклонение непрерывной случайной
величины с законом плотности распределения f(x)
	2х	при	х 0
2е
f (x)
		при	х 0
0
Равно:
#-2
- 1
4

-4 2.2.61.(НТ1). Данное распределение случайной величины

		1					х
					е				при	х 0	Является:
f (x)
									при	х 0
0

#- Показательным

-Нормальным

-Релеевским

2.2.62.(НТ2). Распределение случайной величины, имеющее функцию распределения

	0				ïðè	õ 0
F(x)			x			является:
	1 e				ïðè	õ 0

- Нормальным

#- Показательным

-Равномерным

2.2.63.(НТ1). Математическое ожидание непрерывной случайной величины с плотностью распределения

						õ
		1
					å			ïðè	õ 0
f (x)
								ïðè	õ 0
0

Равно: - /2

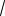# - - /4

2.2.64.(НТ1). Дисперсия непрерывной случайной величины с плотностью распределения

						õ
		1
					å			ïðè	õ 0
f (x)
								ïðè	õ 0
0

Равно:

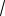# - - /4

2.2.65.(НТ1). Среднее квадратическое отклонение непрерывной случайной величины с плотностью распределения

õ

1

f (x)

å

ïðè

õ 0

ïðè

õ 0

Равно:

0

# -

- /2

- /4

2.2.66.(НТ1).

Случайная

величина, имеющая плотность распределения

вероятностей

1

(x m)2

2

f (x)

e

2

2

распределена по:

#-нормальному закону -показательному закону -равномерному закону

2.2.67.(НТ1). Случайная величина называется распределенной по нормальному закону, если она имеет плотность распределения:

2

x

x

2

e

2

при х 0

- f

(x)

2

при х 0

0

1

(x m)2

2

#- f (x)

e

2

2

- f

0,x 0

(x)

e x,x 0

2.2.68.(НТ1).

Случайная величина, распределенная по закону

1

(x m)2

2

f (x)

e

2

имеет математическое ожидание:

2

#-M[x] m

-M[x] 2

-M[x]

			2.2.69.(НТ1).						Случайная величина, распределенная по закону
1						(x m)2
							2
f (x)					e	2		имеет дисперсию:

2

-D[x] m

#-D[x] 2

-D[x]

			2.2.70.(НТ1).						Случайная величина, распределенная по закону
1						(x m)2
							2
f (x)					e	2		имеет среднее квадратическое отклонение:

2

-[x] m

-[x] 2

#- [x]

2.2.71.(НТ1). Функцией Лапласа называется следующая функция:

1

x

t2

-F(x)

e

2 dt

2

t2

1

- (x)

e

2 dt

2

#-Ф(x) 1

x

t2

e

2 dt

0

2

2.2.72.(НТ1). Функцией Лапласа имеет следующие свойство:

-Ф(0)=1

#-Ф(0)=0 -Ф(0)=0,5

2.2.73.(НТ1). Функцией Лапласа имеет следующие свойство:

-( x) (x)

#- ( x) (x) - ( x) 1

2.2.74.(НТ1). Функцией Лапласа имеет следующие свойство:

- lim Ô(x) 0,5

x

- lim Ô(x) 1

x

#- lim Ô(x) 0,5

x

2.2.75.(НТ1). Нормально распределенная случайная величина имеет функцию распределения:

-F(x) Ô(x m)

-F(x) 1 Ô(x m)

#-F(x) 0,5 Ф(x m)

2.2.76.(НТ3). Случайная величина, имеющая функцию распределения

F(x) 0,5 Ф(x m) распределена по:

#-нормальному закону -показательному закону -равномерному закону

2.2.77.(НТ1). Нормально распределенная случайная величина принимает:

#-любые значения -только положительные значения

-только отрицательные значения 2.2.78.(НТ1). Кривая нормального распределения симметрична относительно:

#- математического ожидания -дисперсии -среднего квадратического отклонения

2.2.79.(НТ1). При увеличении математического ожидания кривая нормального распределения:

#-сдвинется вправо по оси OX

- сдвинется влево по оси OX -не изменится

2.2.80.(НТ1). При уменьшении математического ожидания кривая нормального распределения:

-сдвинется вправо по оси OX

#- сдвинется влево по оси OX -не изменится

2.2.81.(НТ1). Как вычислить вероятность попадания нормально распределенной случайной величины в произвольный интервал ( ; ):

-P( X ) Ô( m) Ô( m)

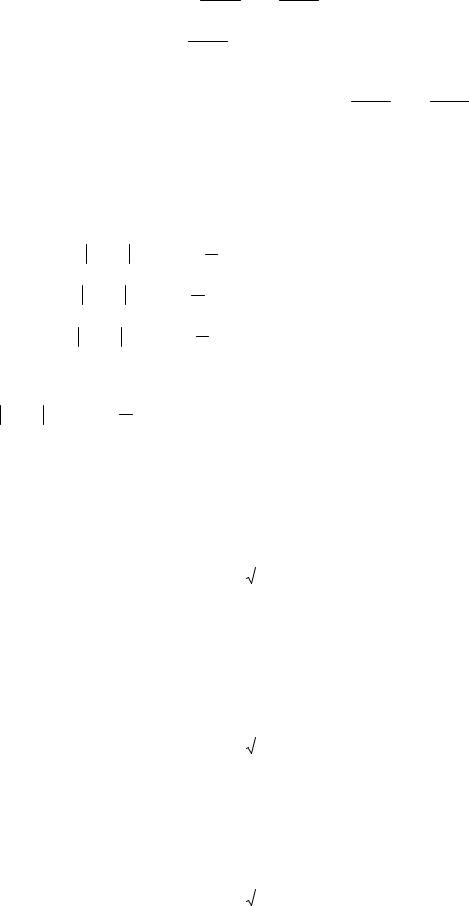
#- P( X ) Ô( m) Ô( m)

-P( X ) Ô( )

2.2.82.(НТ2). Для какой случайной величины вероятность попадания в

интервал вычисляется по формуле P( X ) Ô( m) Ô( m)?

-для распределенной по показательному закону

#- для нормально распределенной

-для распределенной по равномерному закону

2.2.83.(НТ3). Как вычислить вероятность отклонения нормально распределенной случайной величины от математического ожидания на величину, не превосходящую :

#-P[ X m ] 2Ô( )

-P[ X m ] Ô( )

-P[ X m ] 2Ô( )

2.2.84.(НТ2). Для какой случайной величины вероятность отклонения случайной величины от математического ожидания вычисляется по формуле

P[ X m ] 2Ô( )?

-для распределенной по показательному закону

#- для нормально распределенной

-для распределенной по равномерному закону

2.2.85.(НТ1).	Случайная			величина, имеющая плотность распределения
вероятностей							(x 2)2
			1			e
	f (x)						8
	2			2

распределена по:

#-нормальному закону -показательному закону -равномерному закону

2.2.86.(НТ1). Математическое ожидание непрерывной случайной величины с законом плотности распределения f(x)

		1			e	(x 2)2
f (x)						8 равно:
2			2

-

#-2 -0

2.2.87.(НТ1). Дисперсия непрерывной случайной величины с законом плотности распределения

		1			e	(x 2)2
f (x)						8
2			2

Равно:

-8

#-4 -2

2.2.88.(НТ1). Среднее квадратическое отклонение непрерывной случайной величины с законом плотности распределения f(x)

		1			e	(x 2)2
f (x)						8
2			2

Равно: -8 -4

#-2 2.2.89.(НТ1). Данное распределение случайной величиной

				x	2
x
						2
			e 2				при х 0
f (x)								является
		2
							при х 0
0

#- Гауссовским

-Релеевским

-Показательным

2.2.90.(НТ1). Случайная величина Х задана плотностью распределения f(x)

		1		е	х а2
f (x)					2а
		2 а

Вероятность того, что X > a равна: -1/a

-1/(a)2

#-1/2 2.2.91.(НТ1). Случайная величина, имеющая плотность распределения

вероятностей

х а2 f (x) 1 е 2а

2 а

распределена по:

#-нормальному закону -показательному закону -равномерному закону

2.2.92.(НТ1). Математическое ожидание непрерывной случайной величины с законом распределения

		1		е	х а2
f (x)					2а	равно:
		2 а

-а

-а

# - а 2.2.93.(НТ1). Дисперсия непрерывной случайной величины с распределения

		1		е	х а2
f (x)					2а	равно:
		2 а

#-а

-4a

-а

2.2.94.(НТ1). Среднее квадратическое отклонение непрерывной случайной величины с законом распределения

		1		е	х а2
f (x)					2а	равно:
		2 а

-а

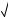#-4a

-а

2.2.95.(НТ1). Закон трех сигм для нормального распределения говорит о том, что событие, состоящее в отклонении нормально распределенной случайной величины от математического ожидания на величину, превышающую утроенное СКО есть событие:

#- практически невозможное -практически достоверное -практически несовместное

2.2.96.(НТ2). Правило трех сигм состоит в том, что нормально распределенная случайная величина содержится в интервале X m 3 с вероятностью:

-1

#- 0,9973

-0,0027

2.2.97.(НТ1). Правило трех сигм состоит в том, что нормально распределенная случайная величина выйдет за пределы интервала X m 3 с вероятностью:

-1

-0,9973

#- 0,0027

2.2.98.(НТ3). По отношению к какому параметру распределения нормальной случайной величины симметричен интервал в законе трех сигм:

#- математическому ожиданию

-дисперсии

-среднеквадратическому отклонению

2.2.99.(НТ3). Какая длина интервала рассматривается в законе трех сигм для нормального распределения:

-3

# - 6

-9

2.2.100.(НТ1). Что означает параметр в законе трех сигм для нормального распределения?

- Математическое ожидание

#-среднее квадратическое отклонение -дисперсия

2.2.101.(НТ2). Событие, состоящее в отклонении нормальной случайной величины от математического ожидания на величину, не превышающую 3 есть событие:

#- близкое к достоверному -близкое к невозможному

-близкое к несовместному.

2.2.102.(НТ2). Событие, состоящее в отклонении нормальной случайной величины от математического ожидания на величину, превышающую 3 есть событие:

- близкое к достоверному

#-близкое к невозможному -близкое к несовместному.

3.1.1. (НТ1).Композицией распределений двух случайных величин X и Y называется распределение случайной величины

#-Z X Y

-Z X Y

-Z X /Y

3.1.2. (НТ2). Композиция распределений для непрерывных и независимых случайных величин вычисляется по формуле:

#- fz (x) fx (x) fY (z x)dx

- fz (x) fx (x) fz (x)dx

- fz (x) fx (x z) fz (z x)dx

3.1.3. (НТ2).Какими должны быть случайные величины X и Y , чтобы

композиция их распределений вычислялась по формуле: fz (x) fx (x) fY (z x)dx?

-непрерывными и зависимыми

#-непрерывными и независимыми -дискретными и независимыми

3.1.4. (НТ1). Если случайные величины X и Y распределены равномерно в

интервале

(-1;1), то в каком интервале композиция распределений этих случайных величин отлична от нуля?

-( 1;1)

-(0;1)

#-( 2; 2)

3.1.5.(НТ1). Композицией любого числа нормальных распределений независимых случайных величин будет:

-равномерное распределение

#-нормальное распределение - показательное распределение.

3.1.6.(НТ1).Композицией двух нормальных распределений независимых случайных величин будет:

-равномерное распределение - показательное распределение.

#-нормальное распределение

3.1.7.(НТ1).Чему равно математическое ожидание композиции пяти

одинаковых нормальных распределений N(m, 2 ) независимых случайных величин?

#- 5m