TVIMS2

4.2.42.(НТ1). Если пара случайных величин, распределенная по двумерному нормальному закону независимы, то про эти случайные величины можно сказать, что они:

#- некоррелированные

-несовместны

-связаны функциональной зависимостью

5.1.1.(НТ 1). Случайная функция X(t) – это

-случайная величина, зависящая от случайного аргумента t -неслучайная функция, зависящая от случайного аргумента t

#-случайная величина, зависящая от неслучайного аргумента t

5.1.2. (НТ 1)

Случайная функция X(t) называется случайным процессом, если

-случайный аргумент t интерпретируется как время

#-неслучайный аргумент t интерпретируется как время -случайная функция и случайный процесс – это одно и то же

5.1.3. (НТ 1)

Реализацией случайного процесса X(t) называется

#-неслучайная функция времени неслучайного аргумента -случайная функция случайного аргумента -неслучайная функция случайного аргумента

5.1.4. (НТ 1)

Сечением случайного процесса называется

-неслучайная величина X(t) при фиксированном значении t t0

-произвольная реализация случайного процесса

#-случайная величина X(t) при фиксированном значении t t0

5.1.5. (НТ 1)

Одномерной плотностью распределения случайного процесса X(t) называется функция

-F(x) P(X(t) x) -F(x) P(X(t) x)

#- f (x; t1) 5.1.6. (НТ 1)

Математическое ожидание m(t) случайного процесса X(t) – это

-случайная функция времени, которая в каждый момент времени t совпадает с математическим ожиданием соответствующей реализации случайного процесса

#-неслучайная функция времени, которая в каждый момент времени t совпадает с математическим ожиданием соответствующего сечения случайного процесса

-случайная функция времени, которая в каждый момент времени t совпадает с математическим ожиданием соответствующего сечения случайного процесса

5.1.7. (НТ 1)

Математическое ожидание m(t) случайного процесса X(t) характеризует

#-поведение случайного процесса X(t) в среднем -поведение случайного процесса X(t) в целом

-максимальное отклонение значений случайного процесса X(t) от D(t)

5.1.8. (НТ 2)

Пусть задан случайный процесс X(t) U t, где U – случайная величина, распределенная равномерно на отрезке 0,1 . Чему равно математическое ожидание этого случайного процесса?

0 t

1 t

#1 t

2

1t

2

5.1.9. (НТ 1)

Пусть m(t) – математическое ожидание случайного процесса X(t). Чему равно математическое ожидание случайного процесса X(t) (t), где (t) – неслучайная функция?

#-m(t) (t)

-(t)m(t)

-m(t)

5.1.10. (НТ 1)

Пусть m(t) – математическое ожидание случайного процесса X(t). Чему равно математическое ожидание случайного процесса (t)X(t), где (t) – неслучайная функция?

-m(t) (t)

#- (t)m(t)

-m(t)

5.1.11. (НТ 1)

Пусть (t) – центрированный случайный процесс. Чему равно его математическое

ожидание?

-m(t) m const

#-m(t) 0 -m(t) 1

5.1.12. НТ 1)
Дисперсией D(t) случайного процесса X(t) называется
-случайная функция времени, которая в каждый момент времени t	совпадает	с
дисперсией соответствующей реализации случайного процесса
-неслучайная функция времени, которая в каждый момент времени t	совпадает	с
дисперсией соответствующей реализации случайного процесса
#-неслучайная функция времени, которая в каждый момент времени t	совпадает	с
дисперсией соответствующего сечения случайного процесса
-случайная функция времени, которая в каждый момент времени t	совпадает	с
дисперсией соответствующего сечения случайного процесса
5.1.13. (НТ 1)

Среднеквадратическое отклонение (t) случайного процесса X(t) характеризует -поведение случайного процесса X(t) в среднем

#-типичное отклонение возможных значений процесса относительно m(t) -максимальное отклонение возможных значений процесса относительно m(t)

5.1.14. (НТ 1)

Как связано среднеквадратическое отклонение (t) случайного процесса X(t) с его дисперсией D(t)?

-(t) D(t)

-(t) D2 (t)

#- (t) 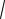D(t) 5.1.15. (НТ 1)

Пусть (t) – среднеквадратическое отклонение случайного процесса X(t). Чему равно среднеквадратическое отклонение случайного процесса (t)X(t), где (t) – неслучайная функция времени?

- (t) (t)

#-| (t)| (t)

-2 (t) (t)

-(t)

5.1.16. (НТ 1)

Пусть (t) – среднеквадратическое отклонение случайного процесса X(t). Чему равно среднеквадратическое отклонение случайного процесса X(t) (t), где (t) –

неслучайная функция?

#- (t)

-(t) (t)

-(t) (t)

-| (t)| (t)

5.1.17. (НТ 1)

Пусть D(t) – дисперсия случайного процесса X(t). Чему равна дисперсия случайного процесса (t)X(t), где (t) – неслучайная функция?

-D(t)

-(t)D(t)

#- 2 (t)D(t)

-| (t)| D(t)

5.1.18. (НТ 1)

Пусть D(t) – дисперсия случайного процесса X(t). Чему равна дисперсия случайного процесса X(t) (t), где (t) – неслучайная функция?

#-D(t)

-D(t) (t)

-2 (t)D(t)

-(t)D(t)

5.1.19. (НТ 2)

Какие из предложенных ниже функций могли бы характеризовать дисперсию некоторого случайного процесса D(t)?

-D(t) sin(t), t 0

-D(t) cos(t), t 0

#-D(t) exp( t), t 0

ни одна из предложенных функций не может характеризовать дисперсию случайного процесса

5.1.20. (НТ 2)

Пусть X(t) – случайный процесс. Известно, что D(t) t , t 0. Чему равна дисперсия случайного процесса X(t) t?

-0

#-t

-t

-2t

5.1.21. (НТ 2)

Пусть задан случайный процесс X(t) Ue t , где U ~ N(1,22 ). Чему равна дисперсия этого случайного процесса?

-e t

-e 2t

-4e t

#-4e 2t

5.1.22. (НТ 1)

Пусть K(t1,t2 ) –корреляционная функция случайного процесса X(t). Какое из следующих утверждений является верным?

#-K(t1,t2 ) K(t2 ,t1)

-K(t1,t2 ) K(t2 ,t1)

-K(t1,t2 ) K(t1,t2 ) 5.1.23. (НТ 1)

Пусть K(t1,t2 ) –корреляционная функция случайного процесса X(t).. Чему равна K(t,t)? -0

-m(t)

#-D(t)

-(t)

5.1.24. (НТ 1)

Пусть K(t1,t2 ) –корреляционная функция случайного процесса X(t).Какое из следующих утверждений является верным?

-R (t1,t2 ) 0 при всех t1,t2

-R (t1,t2 ) 0 при t2 t1

#-R (t1,t2 ) R при всех t1,t2

5.1.25. (НТ 1)

Нормированная ковариационная функция r(t1,t2 ) при совпадении аргументов, т.е. при

t1 t2 , равна: -r(t,t) 0

#-r (t,t) 1

-r(t,t) D(t)

-r(t,t) (t)

5.1.26. (НТ 1)

Корреляционная функция K(t1,t2 ) при совпадении аргументов, т.е. при t1 t2 , равна:

-K(t,t) 0

-K(t,t) 1

#-K(t,t) D(t)

-K(t,t) (t)

5.1.27. (НТ 1)

Пусть известна корреляционная функция K(t1,t2 ) случайного процесса X(t). Для того, чтобы определить дисперсию D(t) случайного процесса:

#-достаточно только K(t1,t2 )

-помимо K(t1,t2 ) необходимо определить математическое ожидание m(t) случайного процесса X(t)

-корреляционная функция K(t1,t2 ) не дает никаких сведений о дисперсии D(t)

5.1.28. (НТ 1)

Пусть известна корреляционная функция K(t1,t2 ) случайного процесса X(t). Какое из следующих утверждений является верным?

Из K(t1,t2 ) можно ли определить математическое ожидание m(t) данного случайного процесса

#Из K(t1,t2 ) можно определить дисперсию D(t) случайного процесса

Из K(t1,t2 ) можно определить и математическое ожидание случайного процесса m(t), и дисперсию D(t)

5.2.1 (НТ 1)

Случайный процесс X(t) называется стационарным в широком смысле, если

-m(t) m const

-m(t) m const, K(t1,t2 ) K(t2 ,t1)

#-m(t) m const, K(t1,t2 ) K(t2 t1)

-m(t) m const, K(t1,t2 ) K(t2 t1) 5.2.2 (НТ 1)

Пусть X(t) – эргодический случайный процесс. Тогда для нахождения любой его вероятностной характеристики достаточно знать:

-вероятностные характеристики одного любого сечения X(t)

#-одну любую достаточно длинную реализацию X(t) -несколько достаточно длинных реализаций X(t)

5.2.3 (НТ 1)

Какое из следующих утверждений является верным?

#-Если X(t) – эргодический случайный процесс, то он является стационарным в узком смысле

-Если X(t) – эргодический случайный процесс, то он не является стационарным в узком смысле

-Если X(t) – стационарный в узком смысле случайный процесс, то он является эргодическим

5.2.4. (НТ 2)

Пусть задан стационарный случайный процесс X(t). Какие из следующих формул могут характеризовать его математическое ожидание m(t) и корреляционную функцию

K(t1,t2 )?

-m(t) t, K(t1,t2 ) cos(t1 t2 )

-m(t) 1, K(t1,t2 ) sin(t1 t2 )

-все вышеприведенные утверждения могут характеризовать стационарный случайный процесс

#-ни одно из приведенных выше утверждений не может характеризовать стационарный случайный процесс

5.2.5 (НТ 3)

Известно, что X(t) – стационарный случайный процесс. Какие из следующих формул могут характеризовать его корреляционную функцию K(t1,t2 )?

-K(t1,t2 ) cos(t1 t2 )

-K(t1,t2 ) sin(t1 t2 )

-K(t1,t2 ) exp(|t1 t2 |)

#-ни одна из приведенных выше формул не может быть корреляционной функцией стационарного случайного процесса

5.2.6 (НТ 1)

Будет ли стационарным в узком смысле случайный процесс X(t) U , где U – случайная величина?

#-Да, независимо от того, какое распределение имеет случайная величина U -Нет, независимо от того, какое распределение имеет случайная величина U

-Без данных о законе распределения случайной величины U о стационарности данного случайного процесса ничего сказать нельзя

5.2.7 (НТ 1)

Пусть X(t) – стационарный случайный процесс. Какие из следующих случайных процессов являются стационарными?

-3X(t) 2t

-tX(t)

#-2X(t) 1

5.2.8 (НТ 1)

Пусть X(t) – стационарный белый шум. Тогда

#-его спектральная плотностьS( ) S0 const

-его корреляционная функция K(t1,t2 ) K0 const

-среди вышеперечисленных вариантов нет правильного

5.2.9 (НТ 1)

Пусть известна спектральная плотность S( ) стационарного случайного процесса X(t). Какое из следующих утверждений является верным?

-По известной спектральной плотности S ( ) можно определить математическое ожидание m(t) случайного процесса X(t)

#-По известной спектральной плотности S( ) можно определить дисперсию D(t) случайного процесса X(t)

-По известной спектральной плотности S ( ) можно определить корреляционную функцию K( ) случайного процесса X(t)

5.2.10 (НТ 1)

Пусть известна дисперсия D(t) стационарного случайного процесса X(t). Какое из следующих утверждений является верным?

-По известной дисперсии D(t) можно определить спектральную плотность S( ) случайного процесса X(t)

-По известной дисперсии D(t) можно определить математическое ожидание m(t) случайного процесса X(t)

-По известной дисперсии D(t) можно определить автоковариационную функцию K(t1,t2 ) случайного процесса X(t)

-Все приведенные выше утверждения являются верными

#-Ни одно из приведенных выше утверждений не является верным

5.2.11 (НТ 2)

Пусть задана автоковариационная функция случайного процесса (t):

2,| | T,

K(t1,t2 ) K(t1 t2 ) R ( )

0,| | T.

Является ли данный случайный процесс стационарным в широком смысле? -да -нет

#-данных для определения стационарности данного случайного процесса недостаточно

5.2.12 (НТ 3)

Пусть X(t) – стационарный случайный процесс. Какие из приведенных ниже функций могут характеризовать его корреляционную функцию?

-K(t1,t2 ) (t1 t2 )2

-K(t1,t2 ) (t1 t2 )2

-K(t1,t2 ) sin2 (t1 t2 )

#-ни одна из приведенных выше формул не может характеризовать автоковариационную функцию стационарного случайного процесса

5.2.13 (НТ 1)

Пусть X(t) – стационарный случайный процесс. Какие из приведенных ниже функций могут характеризовать его дисперсию?

-D(t) sint

-D(t) t2

#-D(t) 3

5.2.14 (НТ 3)

Пусть дисперсия стационарного случайного процесса равна D(t) 2. Какие из приведенных ниже формул могут характеризовать корреляционную функцию этого случайного процесса:

-K( ) 2e 2

#-K( ) 2e | |

-K( ) 4e | |

-K( ) 4cos

5.2.15 (НТ 2)

Пусть X(t) – стационарный случайный процесс. Является ли стационарным случайный процесс t2 X(t)?

-Да всегда

-Да, если m(t) 0

#-Нет

5.2.16 (НТ 2)

Известна автоковариационная функция K(t1,t2 ) 3e |t1 t2| некоторого случайного процесса X(t). Является ли данный случайный процесс стационарным?

-Да -Нет

#-Данных для определения стационарности случайного процесса недостаточно

5.2.17(НТ 2)

Пусть X(t) – стационарный в узком смысле случайный процесс. Будет ли стационарным в узком смысле случайный процесс tX(t 2)?

-Да всегда

-Да, если m(t) 0

#-Нет 5.2.18 (НТ 2)

Пусть задан случайный процесс X(t). Какие из следующих формул могут характеризовать его математическое ожидание m(t) и корреляционную функцию -

K(t1,t2 )?

-m(t) 1, а K(t1,t2 ) sin(t1 t2 ) 2

-m(t) 1, а R (t1,t2 ) sin(t1 t2 ) 2

#m(t) 1, а K(t1,t2 ) cos(t1 t2 ) 2

6.1.1.ТЗ№1 (НТ 1)

Какие операции имеют смысл для данных, измеренных в номинальной шкале?

#-Только x y, x y

-Только x y, x y, x y, x y

- x y, x y, x y, x y, x, x y, x y

6.1.2. (НТ 1)

Какие операции имеют смысл для данных, измеренных в порядковой шкале? -Только x y, x y

#-Только x y, x y, x y, x y

- x y, x y, x y, x y, x, x y, x y

6.1.3. (НТ 1)

Какие операции имеют смысл в количественной шкале? -Только x y, x y

-Только x y, x y, x y, x y

-#x y, x y, x y, x y, x, x y, x y

6.1.4. (НТ 1)

Можно ли применять к признакам, измеренным в количественной шкале, те же методы статистической обработки, что и к признакам, измеренным в порядковой шкале?

#-Да, всегда -Да, в некоторых случаях -Нет

6.1.5. (НТ 1)

Всегда ли можно применять к признакам, измеренным в порядковой шкале, те же методы статистической обработки, что и к признакам, измеренным в количественной шкале? -Да, всегда -Да, в некоторых случаях -#Нет

6.1.6. (НТ 1)

Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется

-выборка

#-генеральная совокупность -статистика

6.1.7.(НТ 1)

Выборка – это

#-последовательность независимых одинаково распределенных случайных величин -конкретный набор данных, полученный в результате эксперимента -генеральная совокупность

6.1.8.(НТ 1)

Последовательность, полученная в результате расположения в порядке неубывания элементов выборки называется -статистический ряд -ряд распределения

#-вариационный ряд

6.1.9. (НТ 1)

Реализация выборки – это -случайным образом отобранные элементы выборки

#-набор конкретных данных, полученных в результате эксперимента -эксперимент, проводимый над выборкой

6.1.10. (НТ 1)

Интервал, в котором заключены все элементы выборки, называется -размах выборки

#-интервал варьирования -объем выборки

6.1.11. (НТ 1)

Пусть X1, X2 , ..., Xn – выборка. Ее объем равен:

#- N

-X(n) X(1)

-Xn X1

6.1.12. (НТ 1)

Номер элемента выборки в вариационном ряду называется -порядок -порядковая статистика

#-ранг

6.1.13. (НТ 1)

Перечень вариантов и соответствующих им частот называется -вариационный ряд

#-статистический ряд -закон распределения

6.1.14. (НТ 1)

Оценкой неизвестной функции распределения является -статистическое распределение -статистический ряд

#-ни один из предложенных вариантов не является верным

6.1.15. (НТ 1)

Статистическое распределение является оценкой:

#-неизвестного закона распределения -неизвестной функции распределения -неизвестных параметров закона распределения

6.1.16. (НТ 1)

Эмпирическая функция распределения случайной величины X – это функция Fn (x),

определяющая для каждого x относительную частоту события

-X x

-X x

#- X x

6.1.17. (НТ 1)

Какое из следующих утверждений является верным?

-Эмпирическая функция распределения может принимать любые значения в интервале

( , )

-Эмпирическая функция распределения может принимать любые значения в интервале

[0, )

#-Эмпирическая функция распределения может принимать любые значения в интервале

[0,1]

6.1.18. (НТ 1)

Какое из следующих утверждений является верным?

#-Эмпирическая функция распределения Fn (x)существует при значениях x ( , )

-Эмпирическая функция распределения Fn (x)существует только при значениях x (0, )

-Эмпирическая функция распределения Fn (x)существует только при значениях x [0,1]

6.1.19. (НТ 1)

Эмпирическая функция распределения -является оценкой вероятности события X x

#-является оценкой вероятности события X x

-определяет относительную частоту события X x

-определяет относительную частоту события X x

6.1.20. (НТ 1)

Гистограмма является приближением -функции распределения -#плотности распределения -статистического распределения