
TVIMS2
.pdf
-10m
-5
3.1.8. (НТ1). Чему равна дисперсия композиции пяти одинаковых нормальных распределений N(m, 2 ) независимых случайных величин?
#- 5 2
-10 2
-5m
3.1.9. (НТ2).Чему равно среднее квадратическое отклонение композиции пяти одинаковых нормальных распределений N(m, 2 ) независимых случайных величин?
-5
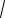 2
2
-5 2
#- 
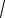 5 2
5 2
3.1.10. (НТ2).В условиях центральной предельной теоремы распределения
случайной величины Zn |
X1 X2 |
... |
Xn mn |
при n стремится к: |
|||||
|
|
|
|
||||||
|
|||||||||
|
|
|
|
|
|
|
n |
||
|
|
#-нормальному |
|||||||
|
|
-равномерному |
|||||||
|
|
-показательному |
|||||||
|
|
3.1.11. (НТ2).При каких n распределение случайной величины |
|||||||
Zn |
|
X1 X2 |
... |
Xn mn |
по условиям центральной предельной теоремы стремиться к |
||||
|
|
|
|||||||
|
|||||||||
|
|
|
n |
||||||
нормальному?
-n 0
#-n
-n 1
3.1.12. (НТ2).Какие формулы можно использовать как приближение при
вычислении вероятности попадания случайной величины Zn |
|
X1 X2 |
... |
Xn mn |
в |
|
|
|
|||
|
|||||
заданный интервал? |
|
|
n |
||
|
|
|
|
|
|
- формулы для равномерного распределения |
|
|
|
|
|
#-формулы для нормального распределения |
|
|
|
|
|
-формулы для показательного распределения. |
|
|
|
|
|
3.1.13.(НТ1).Для какой вероятностной схемы используется в качестве приближения интегральная схема Муавра – Лапласа?
#- для схемы Бернулли -для схемы “ до первого успеха” -для электрической схемы
3.1.14.(НТ1).При какой длине серии испытаний n в схему Бернулли целесообразно использовать интегральную теорему Муавра – Лапласа?
-n 5 -n 10
#-n 10
3.1.15.(НТ1).Как называется функция (x), которая входит в формулу
интегральной теоремы Муавра-Лапласа?
- функция распределения нормальной случайной величины
#-функция Лапласа -плотность распределения нормальной случайной величины
3.1.16. (НТ1).Имя какого русского математика носит центральная предельная теорема – --#-теорема Ляпунова
-теорема Чебышева. -теорема Стеклова
3.2.1.(НТ1).Для каких случайных величин справедливо неравенство Чебышева? - только для нормально распределенных - только для равномерно распределенных
#-для всех
3.2.2.(НТ2).Какое из соотношений описывает сходимость по вероятности последовательности случайных величин Х1, Х2,.., Хn к величине m?
- для любого 0 lim P[ X m ] 1
n
#- для любого 0 lim P[ X m ] 1
n
- для любого 0 lim P[ X m ] 1
n 1
3.2.3.(НТ1).Указать среди перечисленных условий условие, которому должна удовлетворять последовательность случайных величин Х1, Х2,.., Хn в законе больших чисел.
#- случайные величины должны быть независимы -случайные величины должны быть несовместны -случайные величины должны быть некоррелированы
3.2.4.(НТ2).Какой вид сходимости рассматривается в законе больших чисел?
#- по вероятности -по дисперсии
-по математическому ожиданию
3.1.5.(НТ1).Имя какого русского математика носит закон больших чисел? -теорема Ляпунова
#-теорема Чебышева. -теорема Стеклова
3.1.6.(НТ1).Закон больших чисел утверждает, что при большом количестве
испытаний их среднее арифметическое: - не существует
#-мало отличается от математического ожидания - мало отличается от дисперсии
4.1.1.(НТ1). В каком случае говорят, что между двумя случайными величинами X и Y функциональная зависимость?
- если случайные величины X и Y независимы.
#- если каждому значению X соответствует одно значение Y . - если случайные величины X и Y несовместны.
4.1.2. (НТ2). Дискретная случайная величина X имеет распределение:
|
|
2 |
|
|
|
|
|
0 |
|
,2 |
,8 |
|
|
|

Какой закон распределения имеет случайная величина Y X3 ?
-
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
|
,2 |
,8 |
|
|
|
|
#- |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
0 |
|
|
,2 |
,8 |
- |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
,4 |
,6 |
|
|
|
|
4.1.3(НТ2). Дискретная случайная величина X имеет распределение: 2
0
,2 ,8
Найти математическое ожидание случайной величины Y X3 .
-2,4
#- 6,4
-4,2
4.1.4. (НТ2). Дискретная случайная величина X имеет распределение: 2
0
,2 ,8
Найти дисперсию случайной величины Y X3 .
#- 10,24
-7,3
-6.9
4.1.5. (НТ1). Дискретная случайная величина X имеет распределение: 1
1
0
,4 ,6
Какой закон распределения имеет случайная величина Y X2 ?
#-
-
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
,4 |
,2 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
4.1.6. (НТ1). |
|
|
|
||
Дискретная случайная величина X |
имеет распределение: |
||||
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
,2 |
,4 |
,4 |
|
|
|
|
|
|
|
Какой закон распределения имеет случайная величина Y X2 ? |
|||||
#- |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
,4 |
,6 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
,2 |
,4 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
,2 |
,4 |
,2 |
|
|
|
|
|
|
|
4.1.7. (НТ1). Дискретная случайная величина X имеет распределение: |
|||||
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
,2 |
,4 |
,2 |
|
|
|
|
|
|
|
Найти математическое ожидание случайной величины Y X2 .
-1
-0,4
#- 0,6
4.1.8. (НТ2). Дискретная случайная величина X имеет распределение:
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
,2 |
,4 |
,2 |

Найти дисперсию случайной величины Y X2 .
-1
-0,41
#- 0,24
4.1.9. (НТ2). Случайные величины X и Y связаны функциональной
зависимостью Y (X)
плотность распределения
распределения случайной
, где функция у (х) монотонно возрастает. Как найти
fY (y) |
случайной величины Y если известна плотность |
fX (x) |
величины X fX (x)? |
- fY (x) fX g(y) g (y)
#- fY (x) fX g(y) g (y)
#- fY (x) fX g(y) g (y)
4.1.10. (НТ2). Случайные величины X и Y связаны функциональной зависимостью Y (X), где функция у (х) монотонно убывает. Как найти
плотность распределения |
fY (y) |
случайной величины Y , если известна плотность |
распределения случайной |
fX (x) |
величины X fX (x)? |
#- fY (x) fX g(y) g (y)
#- fY (x) fX g(y) g (y)
- fY (x) fX g(y) g (y) .
4.2.1. (НТ1). Две дискретные случайные величины являются независимыми,
если:
- |
p |
|
pX pY |
для всех i и |
j . |
|
|
||||
|
ij |
|
i |
|
j |
|
|
||||
#- |
p |
pX |
pY |
для всех i |
и j . |
|
|
||||
|
ij |
i |
|
j |
|
|
|||||
- |
pij |
|
pji |
для всех i и j . |
|
|
|
||||
4.2.2. (НТ1). Указать, для какого из представленных распределений случайные |
|||||||||||
величины независимы. |
|
|
|
|
|||||||
#- |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Y |
|
1 |
2 |
X |
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0, |
|
|
|
|
|
|
|
|
|
,25 |
,25 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
0 |
0, |
|
|
|
|
|
|
|
|
|
,25 |
,25 |
5 |
|
Y |
0 |
0 |
1 |
,5 |
|
,5 |
|
-

Y |
1 |
2 |
X |
X |
|
|
|
|
|
|
|
0 |
0,3 |
0,2 |
0,5 |
1 |
0,2 |
0,3 |
0,5 |
Y |
0,5 |
0,5 |
1 |
# |
|
2 |
|
Y |
1 |
X |
|
X |
|
|
|
|
|
|
|
0 |
0 |
0,5 |
0,5 |
1 |
0,5 |
0 |
0,5 |
Y |
0,5 |
0,5 |
1 |
4.2.3.(НТ1). Случайная величина X - число дней, которые отработал данный сотрудник в текущем месяце, случайная величина Y - заработная плата данного сотрудника за этот же месяц. Определить характер зависимости между данными случайными величинами.
-независимые
-зависимые функционально
#-зависимые.
4.2.4.(НТ1). Одновременно бросаются две игральные кости. Случайная
величина X - равна числу очков на первом кубике, , случайная величина Y - число очков на втором кубике. Определить характер зависимости между данными случайными величинами.
#- независимые
-зависимые функционально
-зависимые.
4.2.5.(НТ1). Случайная величина X - число равна величине тока, протекающему через данное сопротивление, случайная величина Y - равна падению напряжения на том же сопротивлении. Определить характер зависимости между данными случайными величинами.
- независимые
#- зависимые функционально - зависимые.
4.2.6.(НТ1). Что называется смешанным центральным моментом двцух случайных величин?
#- M ( X M x )(Y M Y )
-M XY
-D ( X M x )(Y M Y )
4.2.7.(НТ1). Как вычисляется коэффициент ковариации двух случайных
величин?
- cov( X ,Y ) M XY
#- cov( |
X ,Y ) M ( X M x )(Y M Y ) |
- cov( |
X ,Y ) D ( X M x )(Y M Y ) |
4.2.8.(НТ1). Как вычисляется коэффициент связи двух случайных величин?
#- cov( |
X ,Y ) |
M ( X M x )(Y M Y ) |
- cov( |
X ,Y ) |
D ( X M x )(Y M Y ) |
- cov( |
X ,Y ) |
M XY |
4.2.9.(НТ2). Случайная величина X измеряется в метрах, а случайная величина Y в секундах. В каких единицах измеряется коэффициент ковариации?
#- м с
-м2 с2
-безразмерный
4.2.10.(НТ2). Случайную величина X увеличили вдвое, а случайную величинуY втрое. Как изменится коэффициент ковариации?
-не изменится
-увеличится в пять раз
#- увеличится в шесть раз.
4.2.11.(НТ2). Случайную величина X увеличили вдвое, а случайную величину Y уменьшили вдвое. Как изменится коэффициент ковариации?
#- не изменится
-увеличится в два раза
-уменьшится в два раза.
4.2.12.(НТ2). . Случайную величина X уменьшили вдвое, а случайную величину уменьшили Y втрое. Как изменится коэффициент ковариации?
-не изменится
-уменьшится в пять раз
#- уменьшится в шесть раз.
4.2.13.(НТ1). Как записывается формула для дисперсии суммы двух
произвольных случайных величин? - D X Y D X D Y
#- D X Y D X D Y 2cov(X,Y) - D X Y D X D Y
4.2.14.(НТ1). . Как записывается формула для дисперсии разности двух
произвольных случайных величин? - D X Y D X D Y
#- D X Y D X D Y 2cov(X,Y) - D X Y D X D Y
4.2.15.(НТ1). Какие из указанных значений может принимать коэффициент корреляции?
#- 0,3
#- 1
-3,2
4.2.16.(НТ1). Случайную величина X увеличили вдвое, а случайную величинуY втрое. Как изменится коэффициент корреляции?
#- не изменится
-увеличится в пять раз
-увеличится в шесть раз.
4.2.17.(НТ1). Случайную величина X увеличили вдвое, а случайную величинуY уменьшили вдвое. Как изменится коэффициент корреляции?

#- не изменится
-увеличится в два раза
-уменьшится у два раза.
4.2.18.(НТ1). Случайную величина X уменьшили вдвое, а случайную величину уменьшили Y втрое. Как изменится коэффициент корреляции?
#- не изменится
-уменьшится в пять раз
-уменьшится в шесть раз.
4.2.19.(НТ1). Если для двух случайных величин коэффициент корреляции равен нулю, то случайные величины называются:
- независимыми
#-некоррелированными -несовместными.
4.2.20.(НТ1). Если коэффициент корреляции отличен от нуля, то случайные величины называются:
-зависимыми
-совместными
#-коррелированными.
4.2.21.(НТ1). Чему равен коэффициент корреляции, если случайные величины независимы?
#- 0
-1
--1
4.2.22.(НТ1). Если две случайные величины X и Y связаны произвольной функциональной зависимостью, то про них можно сказать, что они:
#- зависимы
-коррелированны
-независимы.
4.2.23.(НТ1). Если две случайные величины X и Y связаны линейной зависимостью Y aX b, то про них можно сказать, что коэффициент корреляции равен:
-r 0
#- r 1
-r 3
4.2.24.(НТ1). . Если две случайные величины X и Y связаны линейной зависимостью Y 2X 3, то про них можно сказать, что коэффициент корреляции равен:
- |
r 1 |
#- |
r 1 |
-r 0
4.2.25.(НТ1). Если две случайные величины X и Y связаны линейной зависимостью, то про них можно сказать, что коэффициент корреляции равен:
#- r 1
- |
r 1 |
|
- |
r 0 |
|
4.2.26.(НТ1). |
Что можно сказать про случайные величины, если их |
|
коэффициент корреляции равен r 1? |
||
- |
независимы |
|
#- |
Y aX b |
|
- |
Y X2 |
|
4.2.27.(НТ1). |
Что можно сказать про случайные величины, если их |
|
коэффициент корреляции равен r 1?
#- Y aX b
-Y X2
-независимы.
4.2.28.(НТ1). Можно утверждать, что чем ближе модуль коэффициента к единице, тем ближе зависимость двух случайных величин к:
-квадратичной
-кубической
#- линейной.
4.2.29.(НТ1). Коэффициент корреляции двух случайных величин отрицателен,
если при увеличении одной случайной величины вторая случайная величина
-неизменна
-имеет тенденцию к увеличению
#- имеет тенденцию к уменьшению.
4.2.30.(НТ1). Коэффициент корреляции двух случайных величин положителен, если при увеличении одной случайной величины вторая случайная величина
- неизменна
#- имеет тенденцию к увеличению - имеет тенденцию к уменьшению.
4.2.31.(НТ1). Вероятность попадания двумерной случайной величины в произвольную область G вычисляется как:
#- f (x, y)dxdy
G
-f (x, y)dxdy
-f (x, y)dxdy
0 0
4.2.32.(НТ1). Двумерная плотность распределения для пары случайных величин может быть:
#- f (x; y) 0
#- f (x; y) 0 - f (x; y) 0
4.2.33.(НТ1). По свойству плотности распределения двумерной случайной
величины интеграл f (x, y)dxdy означает:
G
#- вероятность попадания в область G
-площадь области G
-нормирующее свойство для плотности распределения.
4.2.34.(НТ1). Чему равен объем фигуры, заключенной между поверхностью распределения и плоскостью XOY ?
-100
#- |
1 |
|
- |
0 |
|
|
|
|
4.2.35.(НТ1). |
Чему равен интеграл f (x, y)dxdyот плотности |
|
|
|
|
распределения двумерной случайной величины?
#- 1
-0
-10
4.2.36.(НТ1). Двумерная случайная величина распределена равномерно в области G . Чему равна плотность распределения внутри этой области?
- 1
#- |
1 |
, где SG - площадь этой области. |
|
||
|
SG |
|
-0
4.2.37.(НТ1). Двумерная случайная величина распределена равномерно в области G . Чему равна плотность распределения за пределами этой области?
- 1
- |
1 |
, где SG - площадь этой области. |
|
||
|
SG |
|
#- |
0 |
|
4.2.38.(НТ1). По какой формуле можно вычислить закон распределения составляющей Y для пары непрерывных случайных величин?
#- f Y x f x, y dy
- f Y (y) f x, y dx
-f Y (y) f (x, y)dxdy
4.2.39.(НТ1). По какой формуле можно вычислить закон распределения составляющей X для пары непрерывных случайных величин?
#- f X x f x, y dy
- f Y (y) f x, y dx
-f X (x) f (x, y)dxdy 1
4.2.40.(НТ1). Две непрерывные случайные величины независимы, если: - f x, y f X x f Y y
#- f x, y f X x f Y y - f x, y 0
4.2.41.(НТ1). . Если пара случайных величин , распределенная по двумерному нормальному закону имеет коэффициент корреляции равный нулю, то про эти случайные величины можно сказать, что они:
#- независимые
#- некоррелированные - несовместные.
