Про AA-tree

Про AA-дерево было сказано, что «из-за дополнительного ограничения операции реализуются проще чем у красно-черного дерева (за счет уменьшения количества разбираемых случаев)». Мне, однако, кажется, что AA-дерево заслуживает отдельной статьи. Почему? Потому, что фактически это самое быстрое (или одно из самых быстрых) бинарное дерево с простой реализацией.  Я оставлю за рамками данной статьи рассмотрение алгоритмов вставки и удаления в AVL и красно-черное дерево, но их реализация, как правило, не тривиальна. Почему? Как известно, основная проблема бинарного дерева — его балансировка, то есть противодействие вырождению в обычный связный список. Обычно при балансировке дерева возникает много вариантов взаимного расположения вершин, каждый из которых нужно учесть в алгоритме отдельно. AA-дерево было придумано Arne Andersson, который решил, что для упрощения балансировки дерева нужно ввести понятие уровень(level) вершины. Если представить себе дерево растущим сверху вниз от корня (то есть «стоящим на листьях»), то уровень любой листовой вершины будет равен 1. В своей работе Arne Andersson приводит простое правило, которому должно удовлетворять AA-дерево: К одной вершине можно присоединить другую вершину того же уровня но только одну и только справа. (В своей статье автор AA-дерева использует немного другую терминологию, связанную с 2-3 деревьями, но суть не меняется). Таким образом, введенное понятие уровня вершины не всегда совпадает с реальной высотой вершины (расстояния от земли), но дерево сохраняет балансировку при следовании правилу «одна правая связь на одном уровне».  Для балансировки АА-дерева нужно всего 2 (две) операции. Нетрудно их понять из правила «одна правая одноуровневая связь»: это устранение левой связи на одном уровне и устранение двух правых связей на одном уровне.  Это операции названы в оригинальной работе skew и split, соответственно. На приведенных рисунках горизонтальная стрелка обозначает связь между вершинами одного уровня, а наклонная (вертикальная) — между вершинами разного уровня. 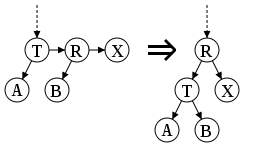skew, устранение левой связи на одном уровне split, устранение двух правых связей на одном уровне Давайте посмотрим как выглядит вставка и удаление в АА-дерево. Для упрощения реализации введем понятие вершины bottom("земля"). Ее уровень всегда 0 и ее левая и правая связь указывают на нее же. Все листовые вершины ссылаются на bottom вместо того, чтобы хранить 0 в ссылке. В рамках недель Delphi на Хабре, исходный код будет в виде псевдокода, похожего на Delphi (для влюбленных в кофе C++: операцияP^.x в Delphi эквивалентна P->x, var означает что переменная передается по ссылке, а не по значению, т.е. при изменении меняется внешняя переменная). Определим вершину AA-дерева. AA-дерево

Утверждается что AA-дерево - это упрощёная версия RB-дерева, у которого не бывает левых красных узлов (или правых, не помню, да и не важно). Поскольку RB-дерево имитирует работу B-дерева четвёртой степени. То AA-дерево не имея один из красных узлов в тройках, имитирует работу 2-3 дерева (как частный случай B-дерева).

Проще говоря у нас есть обычное бинарное дерево поиска, где некоторые узлы имеют две ссылки, а некоторые узлы групируются в пары и пара содержит три ссылки. Таким образом сохраняются все свойства 2-3 узлов, где нелистовые вершины имеют либо одно значение и две ссылки, либо два значения и три ссылки.

Работа

Для работы с AA-деревом существует много способов, некторые из них короткие, некоторые сложны, но более оптимальны. Мы будем делать упор на предельно простую реализацию. Сходство в B-деревом и AA-деревом, будет не очень сильным. Каждый узел содержит в себе свою высоту, расстояние от листьев до этого узла. Все листья на одинаковой глубине от корня, поэтому у корня высота максимальная, а у листьев еденичная (или нулевая если считать с нуля, проще говоря никакая).

Для работы с деревом применяется всего два преобразования:

Skew

Переупорядочивает узел имитируемого 2-3 дерева, если они идут в непоходящем для нас порядке.

Split

Разделяет узел 2-3 дерева, если они сгрупированы в слишком большом количестве.

Вставка

Как и положено почти любому дереву поиска, вставляем новое значение среди листьев дерева (приписывая ему минимальную высоту). Потом вызываем Split (вернее Split(Skew()) ) для всех узлов по пути от листа до корня. Чем имтируем обычное расщепление 2-3 узлов.

Удаление

Сначала мы находим узел, который надо удалить, потом находим минимальное (или максимальное - не важно) значение в одной из его веток, и ставим его на замену удалённому узлу. Всё как в обычном бинарном дереве поиска. На этом сходство с обычными 2-3 деревьями и RB-деревьями практически заканчивается. Вместо того чтобы делать слияние и расщепление узлов, мы стаскиваем все 2-3 узлы, от листа до корня, по цепочке, отчего все попавшиеся узлы сливаются с соседями, рядом с которыми они упали. Стаскиваются по правде не все узлы, а только те у которых после удаления или стаскивания, остался разрыв между уровнями. Т.е. это в чём-то похоже на набору с B-деревом, но это не так как это делают обычно. Поскольку уровень, который расположен за листьями тоже имеет какой-то номер, который ниже листьев, то удаление листа (а физически мы всегда удаляем листы), начинается с того что узел над листом, начал контактировать со слоем, который под листами, из-за этого появляется разрыв, и начинается стаскивание узлов.

После стаскивания мы вызываем Split для каждого узла и приводим дерево в подходящий вид.

...

Так же можно делать всё это, не используя глубину узлов или рекурсию. Но мне это лень, так же как и англискому автору.

Так же как в случае с RB-деревом, можно вместо нулевой сслыки использовать ссылку на фиктивную вершину которая считается нулём. Это поволяет не проверять ссылки на ноль перед тем как с ними работать и немного упростить код. Но на деле прирост скорости и упрощение, от этого крайне незначительны. Код и без того слишком прост. В BeOS (gcc v3 помойму), оба исходника с максимальной оптимизацией, вообще не показали разницы в скорости, так что мне пока нравится именно вариант с нулевыми ссылками, без фиктивных вершин.

aa-tree.cpp - простой образец дерева

aa-tree-z.cpp - дерево с фиктивной нулевой вершиной (разницы почти нет).

simp.pdf - оригинальный документ, с примерами и картинками

Без высот

Можно описать работу с деревом в терминах красно-чёрных вершин. По крайней мере со вставкой это делается просто, как показано ниже. Ну а удаление чуть посложнее, с ним я не нашёл смысла возиться.

node_st::node_st(int v):red(true),p1(0),p2(0),value(v) {}

AA_tree::node_st *AA_tree::Skew(node_st *node)

{

node_st *p1=node->p1;

if(p1 && p1->red) {

p1->red=node->red;

node->red=true;

node->p1=p1->p2,p1->p2=node,node=p1;

}

return node;

}

AA_tree::node_st *AA_tree::Split(node_st *node)

{

node_st *p2=node->p2;

if(p2 && p2->p2 && p2->red && p2->p2->red) {

node->red=node->p2->p2->red=false;

node->p2=p2->p1,p2->p1=node,node=p2;

}

return node;

}

Ограниченная глубина

Для тех кого всё таки как-то напрягает то, что надо хранить глубину в вершинах. Глубина на самом деле используется для поиска разрывов между уровнями и определения соседства вершин. Поэтому для её хранения можно использовать всего два бита, выполняя все операции по кругу. Так же можно не использовать и рекурсию, заменяя её сслыкой на родителя, и даже прекращая подъём по дереву, когда это надо (случаи думаю очевидные). Ниже показаны основные изменения для двухбитных высот (никакие другие строки менять не надо):

struct node_st{

...

unsigned int level:2; //!< высота узла в дереве

//

node_st(int v):level(0),p1(0),p2(0),value(v) {}

unsigned int Level() {return this?level:3;}

};

// Step 3

else if(((node->level-node->p1->Level())&3)==2

|| ((node->level-node->p2->Level())&3)==2) {

if(((node->p2->Level()- --node->level)&3)==1) node->p2->level=node->level;

Единственное что последние для условия можно слегка оптимизировать:

// Step 3

else if((node->level^node->p1->Level())==2 || (node->level^node->p2->Level())==2) {

if(node->p2->Level()==node->level--) node->p2->level=node->level;