Формы представления логических функций.

Для удобства представления логических функций существуют различные формы:

• дизъюнктивная нормальная форма

• конъюнктивная нормальная форма.

Дизъюнктивная нормальная форма (ДНФ) - это сумма произведе­ний, образованных из переменных и их отрицаний. ДНФ не содер­жит скобок.

Например, формы_ - дизъюнктивная нормаль­ная форма, a - нет.

Конъюнктивная нормальная форма (КНФ) - это произведение сумм, состоящих из переменных и их отрицаний.

Например, формы ( a +b)c, ab(c +b), , а- конъюнктивные нормальные формы.

Теорема о ДНФ Всякая сложная логическая функция может быть сведена к ДНФ.

Для того чтобы сделать это, необходимо:

• записать булеву функцию в виде {+, •, -};

• с помощью законов де Моргана спустить черту отрицания до отдельных букв и по закону двойного отрицания уничтожить двойные черточки;

• с помощью первого закона дистрибутивности уничтожить все произве­дения сумм и провести поглошение.

Полученная форма удовлетворяет определению ДНФ.

Если ДНФ функции от n переменных в каждой своей конъюнкции содержит все n переменных либо их отрицания, то это совершенная дизъюнктивная нормальная форма (СДНФ). Каждая функция имеет од ну-единственную СДНФ, и она может быть получена из таблицы истинности этой функции путем записи через знак логического сложения всех наборов переменных, на которых эта функция определена как истинная. Каждый такой набор переменных соответствует конъюнкции,

Например, для функции:

СДНФ по таблице истинности может быть построена как:

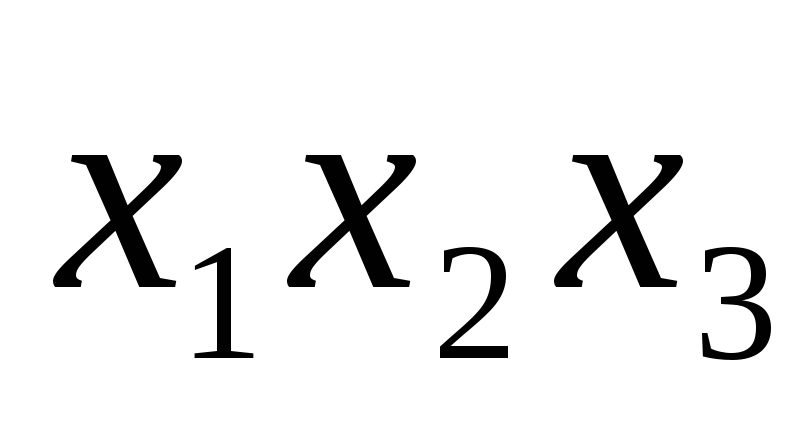
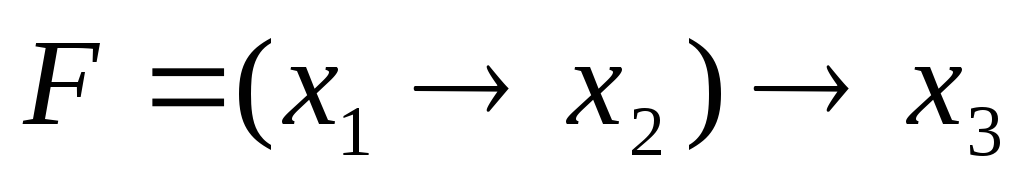
0 0 0	1
0 0 1	0
0 1 0	1
0 1 1	0
1 0 0	1
1 0 1	1
1 1 0	1
1 1 1	0

СДНФ_( F) = 000 + 010 + 100+ 101 +110_=

Теорема о КНФ. Всякая сложная логическая функция может быть сведена к КНФ.

Для того чтобы сделать эго, необходимо:

• записать булеву функцию в виде {+, -, -};

• с помощью законов де Моргана спустить черту отрицания до отдельных букв и по закону двойного отрицания уничтожить двойные черточки;

• с помощью второго закона дистрибутивности уничтожим все суммы произведений и проведем поглощение. Полученная форма удовлетворяет определению КНФ.

Если КНФ функции от n переменных в каждой своей дизъюнкции содержит все n переменных либо их отрицания, то это совершенная конъюнктивная нормальная форма. Каждая функция име­ет одну-единственную СКНФ, и она может быть получена из таблицы ис­тинности этой функции путем записи через знак логического умножения всех наборов переменных, на которых эта функция определена как ложная.

Например, для функции:

СКНФ по таблице истинности может быть построена как

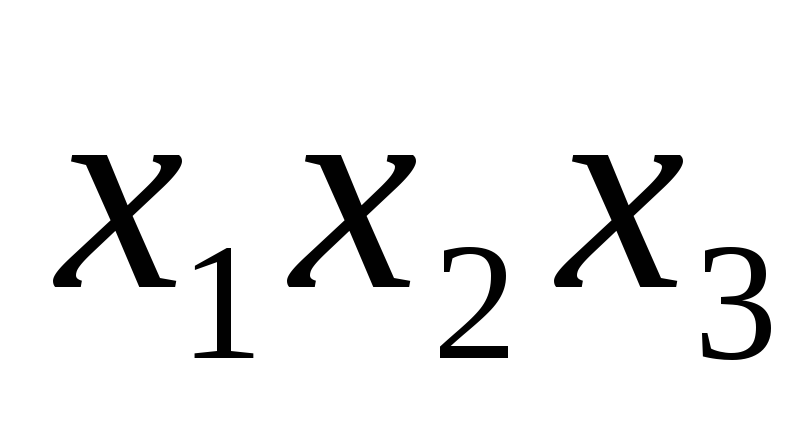
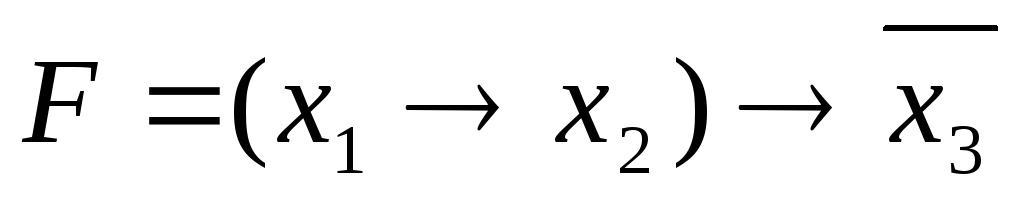
0 0 0	1
0 0 1	0
0 1 0	1
0 1 1	0
1 0 0	1
1 0 1	1
1 1 0	1
1 1 1	0

СКНФ=

Пример. Составить таблицу истинности для формулы:

(X →Y ) & ( Y → Z) v ( Z &X)

Решение.

1. Составим таблицу.

2. Выполним логическую операцию – импликацию (X → Y )

3. Выполним логическую операцию – импликацию ( Y → Z)

4. Выполним логическую операцию – конъюнкцию (X →Y ) & ( Y → Z)

5. Выполним логическую операцию – конъюнкцию ( Z &X)

6. Выполним логическую операцию – дизъюнкцию

(X →Y ) & ( Y → Z) v ( Z &X)

X	Y	Z	X → Y	Y → Z	(X →Y ) & ( Y → Z)	Z &X	(X →Y ) & ( Y → Z) v ( Z &X)
0	0	0	1	1	1	0	1
0	0	1	1	1	1	0	1
0	1	0	1	0	0	0	0
0	1	1	1	1	1	0	1
1	0	0	0	1	0	0	0
1	0	1	0	1	0	1	1
1	1	0	1	0	0	0	0
1	1	1	1	1	1	1	1

Лекция 8. Элементы теории графов

Язык и методы теории графов используются для описания и исследования структурных (комбинаторных) свойств управляющих систем.

Графы - это формальный способ представления систем, состоящих из конечного числа отдельных фрагментов или компонент, между которыми имеют место некоторые связи.

При этом природа связей может быть произвольной для различных систем в разных областях деятельности.

Приведем примеры систем,для которых учет связей между компонентами важен с точки зрения назначения и функционирования систем.

1. Транспортные сети. Их компонентами являются отдельные населенные пункты или объекты, а связями -указание на наличие дорог, которые их соединяют.

2. Молекулы химических соединений. Частями таких систем являются отдельные атомы, составляющие молекулы, а связями — химические соединения между атомами.

3. Электронные схемы. В качестве компонентов в них входят функциональные узлы или элементы, а связи указывают на наличие проводов, соединяющих узлы друг с другом.

4. Административный аппарат учреждения. Здесь частями являются отдельные должностные лица, а связи указывают на наличие должностной подчиненности между сотрудниками учреждения.

Естественная форма наглядного задания систем, представляемых графами, состоит в изображении их на плоскости или в трехмерном пространстве так, чтобы части систем были замкнутыми областями пространства, а связи -дугами. При этом если для связи между частями системы характерно наличие направленности от одной части к другой, то соответствующая дуга снабжается указанием соответствующего направления. Дополнительно требуется, чтобы выбранные области, представляющие части графа, не имели общих точек, а дуги, отражающие связи, не пересекались и не содержали внутри точек областей, соответствующих частям системы.

Изображение системы, для которой выполнены перечисленные условия, называется геометрическим заданием этой системы.

Пример. Возможна следующая система подчиненности по службе сотрудников аппарата управления некоторой фирмы (рис.3):

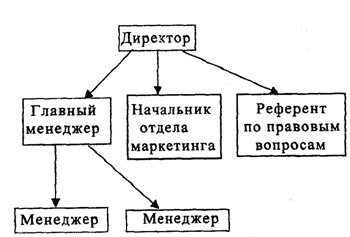
Рисунок 3 – Схема соподчинённостей.

Не случайно теория графов «открывалась» независимо много раз: ее с полным основанием можно считать разделом прикладной ма­тематики. В самом деле, наиболее раннее известное упоминание этой теории встречается в работах Эйлера, и хотя проблему, кото­рой он занимался, можно рассматривать как обычную головоломку, все же она возникла из практики.

Последующие переоткрытия теории графов Кирхгофом и Кэли также уходят своими корнями в реальную действительность. Изу­чение Кирхгофом электрических цепей привело к разработке им основных понятий и получению ряда теорем, касающихся деревьев в графах. В свою очередь Кэли подошел к исследованию деревьев, решая задачи перечисления органических изомеров. Другой под­ход к графам, связанный с рассмотрением головоломок, был пред­ложен Гамильтоном. После этого появилась знаменитая гипотеза четырех красок, которая до сих пор пользуется широкой извест­ностью. В наше столетие также было чрезвычайно много переоткры­тий теории графов. Упомянем кратко некоторые из них, придержи­ваясь хронологического порядка.