Основные свойства функции распределения

1. Функция распределения принимает значения из промежутка 0, 1, т.е.

0 ≤ F(x) ≤ 1.

Это свойство следует из определения функции распределения.

2. Если х₂ >х₁, то

P(x₁≤X<x₂ ) = F(x₂)-F(x₁). (1)

Доказательство. Представим событие, состоящее в том, что случайная величина примет значение, меньшее х_2, в виде суммы несовместных событий –

{: X() < x₂} = {: X() х₁}  {: x₁ ≤ X() < x₂}.

Так как события несовместные, применим аксиому 3 –

P(X < x₂) = P(X  x₁) + P(x₁ ≤ X < x₂),

но P(X < x₂) = F(x₂), P(X  x₁ ) = F(x₁), следовательно

F(x₂) = F(x₁) + P(x₁ ≤ X < x₂), (2)

а это и означает, что P(x₁≤X<x₂ ) = F(x₂)–F(x₁).

4. Функция распределения – неубывающая функция, т.е. если

x₂  x₁ => F(x₂) ≥ F(x₁).

Доказательство. Если x₂  x_1, то справедливо соотношение (2). Но, согласно

аксиоме 1 P(x₁ ≤ X < x₂) ≥ 0,

следовательно, F(x₂) ≥ F(x₁).

5. P(X ≥ x ) = 1-F(x).

Доказательство. События {: X() ≥ x} и {: X() < x} – противоположные события, так как они несовместные и

{: X() ≥ x}{: X() < x} = Ω, следовательно,

Р{: X() ≥ x} + Р{: X() < x}=1, тогда Р(X() ≥ x) = 1–Р(X() < x) = 1 – F(x).

6. Если х  , то .

Доказательство. Пусть x_1, …, x_n …– бесконечно возрастающая числовая последовательность, x_n → ∞ при n → ∞, надо доказать, что .

Рассмотрим последовательность несовместных событий А₁, А₂, …, А_n, …

А₁ = {: X()<x₁}, А₂ = {: x₁ ≤ X() < x₂}, …, A_n = {: x_n-1 ≤ X() < x_n}, n = 3, 4, …

Очевидно, что событие {: X() < x_n} можно представить в виде суммы событий А₁, А₂, …, А_n

{: X() < x_n}= .

Так как события A_i несовместны, то по аксиоме сложения

.

Легко видеть, что событие, равное сумме всех событий А_i, является достоверным событием, т.е.

= Ω.

Тогда по аксиоме 2 и аксиоме 3` имеем

.

Замечание. Мы не пишем , так как не определен предельный переход под знаком вероятности.

6. Если x → - ∞, то F(x) → 0.

7. Функция распределения непрерывна слева, т.е.

.

Свойства 6, 7 можно доказать при помощи аксиомы непрерывности, которая является альтернативной по отношению к аксиоме 3`. То есть в аксиоматику теории вероятностей вместо аксиомы 3` можно включить аксиому непрерывности, тогда аксиому 3` можно будет доказать как теорему и наоборот, аксиому непрерывности можно доказать с использованием аксиомы 3`.

Билет 6

Дискретная случайная величина принимает конечное или счётное множество значений. Пусть Х – дискретная случайная величина, принимающая значения x₁  x₂  … x_n … с вероятностями р₁, р₂, …., р_n ,…, Р(x_i) = p_i, . Если по оси абсцисс отложить x₁, x₂, …, x_n …, а по оси ординат – соответствующие вероятности p_i и соединить соседние точки отрезками, то получим многоугольник распределения дискретной случайной величины (рис.1), который является графическим изображением ряда распределения дискретной случайной величины. Например, если Х – число выпадений «решки» при двух подбрасываниях монеты, то ряду распределения, изображенному на рис. 2 будет соответствовать многоугольник распределения, изображенный на рис. 3.

хi	0	1	2
pi	0.25	0.5	0.25

Рис. 1 Рис.2

Р ассмотрим, что представляет собой функция распределения дискретной случайной величины Х.

Если х  х₁ , то F(x) = P(X x) = 0, так как событие : X x – невозможное.

Если х₁  х  х₂, то событие : X x наступит тогда и только тогда, когда наступит событие : X = x₁, поэтому F(x) = P(X x) = Р X = x₁ = р₁.

Если х₂  х  х₃ , то событие : X x равно сумме событий : X = x₁и : X = x₂. Поэтому F(x) = P(X x) = Р X = x₁ + Р X = x₂ = р₁ + р₂.

Аналогично, если х_i  х  х_i+1, то F(x) = р₁ +р₂+…+р_i.

Таким образом, функция распределения дискретной случайной величины имеет вид

Очевидно, что функция распределения дискретной случайной величины постоянна на промежутках (-, х₁, (х₁, х₂, …, (х_i, х_i+1, … В точках x₁, x₂, …, x_n …, функция распределения имеет скачки, равные вероятности того, что случайная величина примет соответствующее значение. График функции распределения будет иметь вид, схематично изображенный на рис. 4. График функции распределения, соответствующий ряду распределения числа выпадений «решки», изображен на рис. 5.

Равномерное распределение

Определение 1. Случайная величина Х, принимающая значения 1, 2, …, n, имеет равномерное распределение, если P_m = P(Х = m) = 1/n,

m = 1, …, n.

Очевидно, что .

Рассмотрим следующую задачу. В урне имеется N шаров, из них M шаров белого цвета. Наудачу извлекается n шаров. Найти вероятность того, что среди извлечённых будет m белых шаров.

Нетрудно видеть, что .

Гипергеометрическое распределение

Определение 2. Случайная величина Х, принимающая целочисленные значения, имеет гипергеометрическое распределение, если , m = 0, 1, …, min(n, M). Можно показать, что .

Геометрическое распределение

Определение 3. Случайная величина X имеет геометрическое распределение, если

P(Х = m) = P_m= q^m-1p, m = 1, …

где q = 1–p, p(0, 1). Геометрическое распределение имеет случайная величина X, равная числу испытаний по схеме Бернулли до первого наступления успеха с вероятностью успеха в единичном испытании р. Покажем, что Σp_i = 1

.

Билет 7

Распределение Пуассона

Определение 4. Случайная величина Х имеет распределение Пуассона с параметром , если , m = 0, 1, …

Покажем, что Σp_m = 1. .

Биномиальное распределение

Определение 5. Случайная величина X имеет биномиальное распределение, если , m = 0, 1, …, n,

где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1–p.

Распределение Бернулли

Определение 6. Случайная величина Х имеет распределение Бернулли, если P(Х = m) = P_m = p^mq^n-m, m = 0, 1, …, n.

При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то .

Теорема Пуассона. Если n  , а p  0, так что np  , то .

Доказательство. Обозначим _n = np, по условию теоремы , тогда

.

При n  , _n^m  ^m,

Отсюда получаем утверждение теоремы. Р_n(m)  при n  .

Формула Пуассона хорошо приближает формулу Бернулли, если npq  9. Если же произведение npq велико, то для вычисления Р_n(m) используют локальную теорему Муавра–Лапласа.

Локальная теорема Муавра – Лапласа.

Пусть p(0;1) постоянно, величина равномерно ограничена, т.е. с, |x_m|<с. Тогда

,

где (n;m) – бесконечно малая величина, причем .

Из условий теоремы следует, что ,

где , .

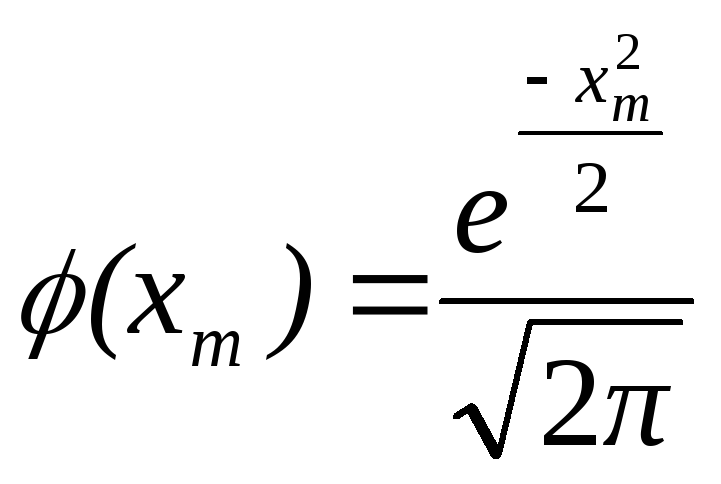Для вычисления Р_n(m) по формуле, приведенной рнее, используют таблицы функции

.

Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.

Решение.

xi	0	1	2	3
рi	0,343	0,441	0,189	0,027

Задача 2. Вероятность поломки произвольного компьютера равна 0,01. Построить ряд распределения числа вышедших из строя компьютеров с общим числом 25.

Решение.

xi	0	1	2	3	4	5	6	…	25
рi (Пуассон)	0,778	0,196	0,024	0,002	0,000	0,000	0,000	0,000	0,000
рi (Бернулли)	0,779	0,195	0,022	0,001	0,000	0,000	0,000	0,000	0,000

Билет 8

Интегральная теорема Муавра – Лапласа. Если вероятность успеха в каждом испытании р, p(0;1) постоянна, то при n   для любых a, b

.

На основании интегральной теоремы Муавра–Лапласа для вычисления вероятности события при больших n и npq 9 используют приближенную формулу

где .

Значения можно найти, воспользовавшись таблицами функции Лапласа, покажем это:

= ,

т.е. при больших n,

Ф(b) – Ф(а). (1)

Значения функции Лапласа приведены в таблицах для х  0. Для того, чтобы вычислить значения функции для отрицательных х, надо воспользоваться следующей теоремой.

Билет 9

Определение 1. Случайная величина X – непрерывная случайная величина, если существует функция p(x)  0, такая что, xR, справедливо соотношение .

Определение 2. Функция p(х) называется плотностью распределения вероятностей непрерывной случайной величины.

1. .

Доказательство вытекает из определения.

2. Плотность распределения p(x) определяет закон распределения непрерывной случайной величины

.

Это свойство также следует из определения плотности р(х).

3. Для любых х₁  х₂ , .

Доказательство. По свойству функции распределения .

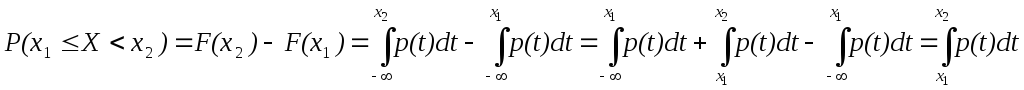4. .

Доказательство: .

6. Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю, т.е.

P(X = a) = 0.

Доказательство. Событие можно представить как . События A_n = a  Х  a + удовлетворят условиям аксиомы непрерывности

A₁  A₂ … A_n …, .

Тогда, применив аксиому, получим

.

Из этого свойства следует, что Р(a<X<b) = P(a≤X<b) = P(a<X≤b) = P(a≤X≤b).

7. Если x – точка непрерывности p(x) и если Δ→0, то

.

Из этого свойства следует, что чем больше значение плотности p(x), тем больше вероятность попадания случайной величины в интервал (x; x + ∆).

Плотностью распределения может быть любая неотрицательная функция, интеграл от которой по всей числовой прямой равен 1, т.е. .

Функция распределения случайной величины любой точке x_p ставит в соответствие вероятность р = F(x_p) = P(X<x_p), т.е. по x_p найти F(x_p). В иных случаях требуется решение обратной задачи  по значению вероятности р найти решение уравнения F(x_p) = р.

Определение 3. Точка x_p, которая является решением записанного уравнения, называется квантилью, отвечающей заданному уровню вероятности р, или р % квантилью распределения F(x).

Из определения непрерывной случайной величины следует, что функция распределения непрерывной случайной величины непрерывна. Поэтому для непрерывной случайной величины для любого р, 0 < p < 1 существует квантиль х_р.

Определение 4. Квантиль, отвечающая вероятности р = ½, называется медианой распределения.

Медиана является одной из характеристик центра распределения случайных величин.

Билет 10