Квадрат волновой функции имеет смысл плотности вероятности, т.Е. Определяет вероятность нахождения частицы в единичном объёме в окрестностях точки с координатами X,y,z.

Интегрируя по объёму, можно определить вероятность нахождения частицы в этом объёме в условиях стационарного поля.

(101)

- условие нормировки ψ-функции.

Уравнение Шредингера

Точный вид волновой функции можно найти, решая уравнение, называемое уравнением Шредингера. Уравнение Шрёдингера в квантовой механике, так же как и второй закон Ньютона в классической механике, не выводится, а постулируется. Стационарное уравнение Шредингера имеет вид

, (102)

где ,Е-полная энергия частицы,U-потенциальная энергия.

Уравнение Шрёдингера связывает ψ-функцию с массой микрочастицы m, её полной энергиейEи потенциальной энергиейU. И зная конкретный вид потенциальной энергии уравнение можно решать. Однако количество задач, допускающих точное решение, очень ограничено.

В уравнение Шрёдингера входит в качестве параметра полная энергия частицы Е. Из теории дифференциальных уравнений следует, что уравнение Шрёдингера имеет решение не при любых значениях энергии, а лишь при некоторых, называемыхсобственными значениями.Решения, соответствующие собственным значениям энергииЕ,называютсобственными функциями задачи.

Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.

Наиболее простым примером на нахождение собственных значений энергии и соответствующим им собственных значений функции является решение задачи о движении частицы в одномерной потенциальной яме.

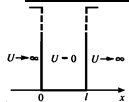Частица может двигаться только вдоль осиХв пределах ширины ямы0<х<l.Внутри ямы пси-функция отлична от нуля, а на границах ямыψ(0)= ψ(l)=0.Внутри ямы силового поля нет (U=0).

Уравнение Шрёдингера для стационарных состояний в пределах ямы имеет вид:

(103)

Рис. 28.

Собственные значения энергии определяются формулой:

(n=1,2,3…) (104)

Таким образом, энергия частицы принимает лишь определённые дискретные значения, т. е. квантуется.

Собственные волновые функции имеют вид:

(n=1,2,3…) (105)

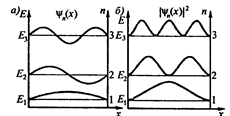
На рис. 29 изображены графики собственных функций (а) и плотность вероятности (б)обнаружения частицы на разных энергетических уровнях в зависимости от расстояния от стенок ямы.

Рис. 29

Атом водорода. Квантовые числа.

Для атома водорода потенциальная энергия имеет вид

И решение уравнения Шредингера предсказывает точно такие же уровни, что и теория Бора:

(106)

n– носит название главного квантового числа, и оно характеризует энергию системы. Но кромеn, при решении появляются еще два квантовых числа. Орбитальное квантовое числоlсвязано с моментом импульса электрона. Оно может принимать значения от 0 доn-1. В основном состоянии сn=1,n=0 приn=3, 1=0,1,2. Величина момента импульсаL связана с числомlсоотношением

(107)

Магнитное квантовое mчисло характеризует проекцию момента импульса

(108)

и может принимать значения от –1 до +1. Например, l=2,m=-2,-1,0,1,2. Название магнитного квантового числа заимствовано из опыта: было обнаружено, что при газовом разряде спектральные линии расщепляются в магнитном поле на несколько линий, расположенных близко друг к другу (эффект Зеемана).

Есть еще спиновое квантовое число m_S, которое принимает лишь два значенияи -. Существование этого квантового числа не следует из уравнения Шредингера. Указание о необходимости введенияm_Sвпервые было получено из опыта. Тщательное исследование спектральных линий атома водорода показало, что каждая линия в действительности состоит из двух (или большего числа) линий. Это явление получило название тонкой структуры.