Деление ядер и цепная реакция

В 1938 году Отто Ган и Штрассман сделали удивительное открытие. Они обнаружили, что при бомбардировке урана нейтронами иногда возникают, примерно, вдвое более легкие ядра, чем исходное ядро урана. Лиза Майтнер и Фриш быстро поняли, что происходит: ядро урана, поглотив нейтрон, распадается на две части (примерно). Такое превращение выглядело необычным, так как все известные тогда превращения сопровождались вылетом из ядра лишь небольших осколков (n,p или). Новое явление было названо делением ядра. Оказалось, что изотопделится легче, чем более распространенный. Образовавшиеся ядраN₁иN₂называют осколками.

. (111)

Время жизни промежуточного ядра равно 10^-12с. Осколки могут быть разной природы

(112)

В результате реакции деления высвобождается огромное количество энергии, так как масса ядра значительно больше суммарной массы осколков деления. Разность масс порядка 0,9 Мэв на нуклон, а для 236 нуклонов получим около 200 Мэв. Для ядерных масштабов это огромная энергия. И если одновременно делится большое число ядер урана то в макроскопических масштабах будет выделяться огромная энергия. Физики (Ферми) поняли что нейтроны, испускаемые в каждом акте деления можно использовать для цепной реакции: один нейтрон вызывает деление одного ядра урана; два или три образовавшихся нейтрона вызовут дополнительные акты деления и так далее. И процесс будет лавинообразно нарастать. В 1942 Ферми с сотрудниками запустили первый ядерный реактор. Разница между ядерным реактором и атомной бомбой заключается в скорости высвобождения энергии. Для производства взрыва достаточно сблизить две подкритические массы.

Ядерный синтез

Масса любого стабильного ядра меньше суммы составляющих его протонов и нейтронов. Следовательно, если два протона и два нейтрона привести в соприкосновение, чтобы образовалось ядро гелия, то это сопровождалось бы уменьшением массы, что проявится в выделении огромного количества энергии. Образование ядер в процессе слияния отдельных протонов и нейтронов или легких ядер называется ядерным синтезом. В настоящее время ядерный синтез идет в недрах звезд в том числе и Солнца.

Примеры решения задач.

Пример 1 По длинному прямому тонкому проводу течёт ток силой . Определить магнитную индукцию B поля, создаваемого проводником в точке, удалённой от него на расстояние .

Решение. Магнитное поле, создаваемое прямым бесконечно длинным проводником ничтожно малого сечения, обладает осевой симметрией. Это значит, что модуль вектора магнитной индукции в данной точке будет зависеть только от её расстояния до проводника. Поэтому все точки на окружности радиуса r, лежащей в плоскости, перпендикулярной проводнику (рисунок 1), будут характеризоваться одинаковой по модулю магнитной индукцией

.

Н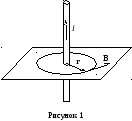аправление вектораB зависит от положения точки на окружности и направления тока в проводнике. Этот вектор направлен по касательной к проведённой нами окружности (это следует из закона Био-Савара-Лапласа, записанного в векторной форме). Окружность на рисунке 1.1 является магнитной силовой линией. Её направление (а значит, и направление вектора B) определяется по правилу правого винта.

Произведём вычисления:

.

Ответ: .

Пример 2 Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой , расположены на расстоянии друг от друга. Определить магнитную индукциюB поля, создаваемого проводниками с током в точке A, отстоящей от оси одного проводника на расстоянии , от оси другого –(рисунок 2).

Р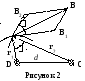ешение. Для нахождения магнитной индукцию B в точке A воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций B₁ и B₂ полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:

.

Модуль вектора B может быть найден по теореме косинусов:

.

Магнитные индукции (если не указана среда, то имеется в виду, что проводник находится в вакууме, и следовательно, )B₁ и B₂ выражаются соответственно через силу тока и расстояния r₁ и r₂ от проводов до точки A:

, .

Подставляя выражения B₁ и B₂ в формулу и вынося за знак корня, получаем

.

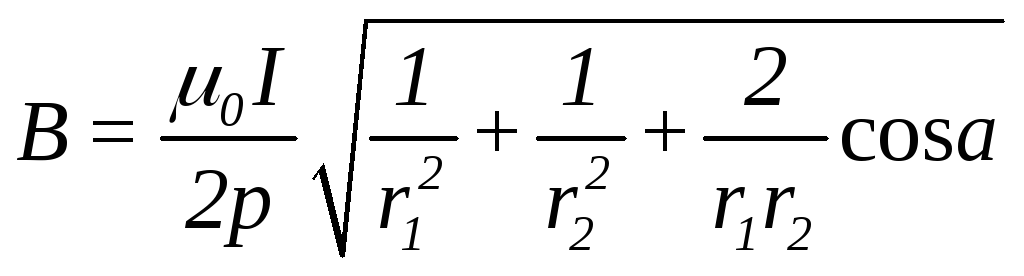Вычислим cos. Заметив, что (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем

,

где d – расстояние между проводами. Отсюда

.

Подставим в формулу числовые значения физических величин и произведём вычисления

Ответ: .

Пример 3 По проводу, согнутому в виде квадрата со стороной , течёт ток силой. Найти магнитную индукцию B в точке O пересечения диагоналей квадрата.

Решение. Расположим квадратный виток в плоскости чертежа (рисунок 3). Согласно принципу суперпозиции магнитных полей

,

г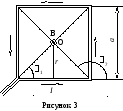деB₁, B₂, B₃, B₄ – магнитные индукции полей, создаваемых токами, протекающими по каждой стороне квадрата.

В точке O пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости чертежа «к нам». Кроме того, из соображений симметрии следует, что модули этих векторов одинаковы: . Это позволяет векторное равенство заменить скалярным

.

Магнитная индукция поля, создаваемого отрезком прямолинейного провода с током, выражается формулой

.

Учитывая, что и(рисунок 3.19), формулу можно переписать в виде

.

Подставив выражение B₁ в формулу , найдём

.

Заметив, что и(так как), получим

.

Произведём вычисления

.

Ответ: .

Пример 4 Плоский квадратный контур со стороной , по которому течёт ток силой, свободно установился в однородном магнитном поле с индукцией . Определить работуA, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон на угол: а) ; б). При повороте контура сила тока в нём поддерживается неизменной.

Решение. Как известно на контур с током в магнитном поле действует момент силы (рисунок 4):

,

где – магнитный момент контура;

B – величина магнитной индукции;

 – угол между векторами p_m (направлен по нормали к контуру) и B.

П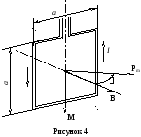о условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (), а значит , т.е. векторы p_m и B сонаправлены (параллельны). Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота ), то для подсчёта работы применим формулу работы в дифференциальной форме .

Учитывая формулу , получаем

.

Взяв интеграл от этого выражения, найдём работу при повороте на конечный угол:

.

Работа при повороте на угол равна

.

Выразим числовые значения величин в единицах системы СИ: ,,, и подставим в :

.

Для вычисления работы при повороте на угол , учитывая, что угол₂ мал, заменим в выражении :

.

Выразим угол ₂ в радианах. После подстановки числовых значений в , найдём

.

Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур:

,

где ₁ – магнитный поток, пронизывающий контур до перемещения;

₂ – то же самое после перемещения.

Если , то ,. Следовательно,, что совпадает с .

Ответ: ;;.

Пример 5 Электрон, пройдя ускоряющую разность потенциалов , попал в однородное магнитное поле напряжённостью. Определить радиус кривизны траектории и частотуn обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца F_Л (действием силы тяжести можно пренебречь), которая перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона , гдеa_n – нормальное ускорение, или

,

где e – элементарный заряд;

v – скорость электрона;

B – магнитная индукция;

m – масса электрона;

R – радиус кривизны траектории;

 – угол между векторами v и B (в данном случае и,).

Из формулы найдём

.

Входящий в равенство импульс mv может быть выражен через кинетическую энергию T электрона:

.

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством

.

Подставив выражение T в формулу , получим

.

Магнитная индукция B может быть выражена через напряжённость H магнитного поля в вакууме

.

где ₀ – магнитная постоянная.

Подставив выражения B и mv в формулу , определим радиус кривизны траектории

.

Произведём вычисления:

.

Для определения частоты обращения воспользуемся формулой, связывающей частоту со скоростью и радиусом:

.

Подставив в формулу выражение , получим

.

Произведём вычисления:

Ответ: ;.

Пример 6 В однородном магнитном поле () равномерно с частотой вращается рамка, содержащая витков, плотно прилегающих друг к другу. Площадь рамки равна . Определить мгновенное значение э.д.с. индукции ₁, соответствующее углу поворота рамки .

Решение. Мгновенное значение э.д.с. индукции _i определяется из закона электромагнитной индукции Фарадея

,

где  – потокосцепление.

Потокосцепление  связано с магнитным потоком  и числом N витков, плотно прилегающих друг к другу, соотношением

.

Подставляя выражение  в формулу , получаем

.

При вращении рамки магнитный поток , пронизывающий рамку в момент времени t, определяется соотношением

,

где B – магнитная индукция;

S – площадь рамки;

 – циклическая частота вращения рамки.

Подставив в формулу выражение  и продифференцировав полученное выражение по времени, найдём мгновенное значение э.д.с. индукции

.

Циклическая частота  связана с частотой вращения n соотношением

.

Подставив выражения  в формулу и заменив t на , получим

.

Произведём вычисления:

.

Ответ: .

Пример 7 Соленоид с сердечником из немагнитного материала содержит витков провода, плотно прилегающих друг к другу. При силе тока магнитный поток. Определить индуктивностьL соленоида и энергию W магнитного поля соленоида.

Решение. Индуктивность L связана с потокосцеплением  соотношением

.

Потокосцепление, в свою очередь, может быть определено через поток  и число витков N (при условии, что витки плотно прилегают друг к другу):

.

Из формул и находим индуктивность соленоида:

.

С учётом энергия магнитного поля соленоида равна

.

Подставим в формулы и значения физических величин и произведём вычисления:

;

.

Ответ: ;

Пример 8. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. На линзу нормально падает монохроматический свет. Определить длину волны света (мкм), если радиус пятого светлого кольца Ньютона в отражённом свете равен 3 мм. Радиус кривизны линзы R= 4 м.

Решение. Радиус m-го светлого кольца Ньютона в отражённом свете определяется по формуле

,

Из этой формулы сразу находим

.

Подставляя сюда значения, получаем

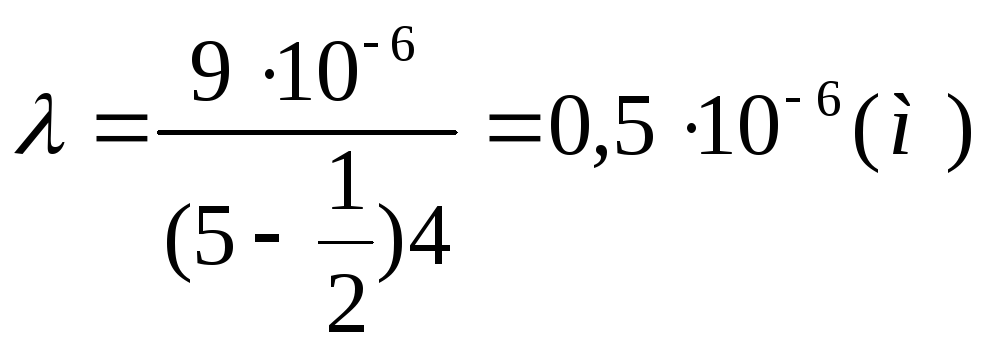
Ответ: 0,5 мкм.

Пример 9. От двух когерентных источников S₁ и S₂ () лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную плёнку (), интерференционная картина изменилась на противоположную. При какой наименьшей толщинеd_min плёнки это возможно?

Решение. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечётное число половин длин волн, т.е.

,

где ₁ – оптическая разность хода пучков световых волн до внесения плёнки;

₂ – оптическая разность хода тех же пучков после внесения плёнки;



Наименьшей толщине d_min плёнки соответствует . При этом формула примет вид

.

Выразим оптические разности хода ₁ и ₂. Из рисунка 4.3 следует

,

.

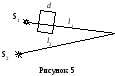
Подставим выражения ₁ и ₂ в формулу :

.

Отсюда

.

Произведём вычисления:

.

Ответ: .

Пример 10 На стеклянный клин с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны . Числоm возникающих при этом интерференционных полос, приходящихся на 1 см, равно . Определить угол клина.

Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отражённые пучки света когерентны. Поэтому на поверхности клина будут наблюдаться интерференционные полосы. Так как угол клина мал, то отражённые пучки 1 и 2 света (рисунок 6) будут практически параллельны.

Т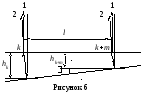ёмные полосы видны на тех участках клина, для которых разность хода лучей кратна нечётному числу половин длин волн:

,.

Разность хода  двух волн складывается из разности оптических длин путей этих волн () и половины длины волны (). Величинапредставляет собой добавочную разность хода, возникающую при отражении световой волны 1 от оптически более плотной среды. Подставляя в формулу разность хода световых волн, получаем

,

где n – показатель преломления стекла ();

d_k – толщина клина в том месте, где наблюдается тёмная полоса, соответствующая номеру k;

i₂ – угол преломления.

Согласно условию угол падения равен нулю, следовательно, и угол преломления i₂ равен нулю, а . Раскрыв скобки в правой части равенства , после упрощения получим

.

Пусть произвольной тёмной полосе k-го номера соответствует толщина d_k клина, а тёмной полосе (k+m)-го номера – толщина d_k+m клина. Тогда из рисунка 4.4, учитывая, что m полос укладывается на расстоянии l, найдём

.

Выразим из d_k и d_k+m и подставим их в формулу . Затем, учитывая, что (из-за малости угла), получим

.

Подставляя значения физических величин, найдём

.

Выразим  в градусах. Для этого можно воспользоваться соотношением между радианом и секундой (таблица Б3)

.

Тогда

.

Ответ: .

Пример 11 На дифракционную решётку в направлении нормали к её поверхности падает монохроматический свет. Период решётки . Определить наибольший порядок дифракционного максимума, который даёт эта решётка в случае красного () и в случае фиолетового () света.

Решение. Из формулы, определяющей положение главных максимумов дифракционной решётки, найдём порядок m дифракционного максимума:

,

где d – период решётки;

 – угол дифракции;

 – длина волны монохроматического света.

Так как не может быть больше 1, то числоm не может быть больше d/, т.е.

.

Подставив в формулу значения, получим:

(для красных лучей);

(для фиолетовых лучей).

Если учесть, что порядок максимумов является целым числом, то для красного света , а для фиолетового.

Пример 12Какова должна быть наименьшая ширинаl_min дифракционной решетки, выраженная в миллиметрах, чтобы прибор с такой решеткой мог разрешить линии дублета натрия с длинами волн λ₁=589,0 нм и λ₂=589,6 нм ?

Решение.

Две близко расположенные линии λ₁ и λ₂ в спектре будут разрешенными, если разрешающая способность прибораRне меньше, чем

,

где λ – среднее значение двух линий, а δλ- их разность.

Известно, что разрешающая способность дифракционной решетки

R=mN,

где m- порядок спектра,N- число штрихов решетки, которое выражается через ширину решеткиlи период решеткиd.

Исходя из формулы дифракционной решетки

dsinφ=mλ,

максимальный порядок m_maxбудет наблюдаться при.Тогдаm_max=d/λ и

.

Таким образом, две линии в спектре будут разрешены, если R_max≥R

=

Отсюда следует

Произведя вычисления, получим l_min= 0.58 мм.

Пример 13 Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отражённый от пластины пучок света образует угол с падающим пучком (рисунок 7). Определить показатель преломленияn₁ жидкости, если отражённый свет максимально поляризован.

Р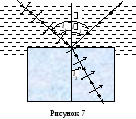ешение. Согласно закону Брюстера пучок света, отражённый от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному показателю преломления n₂₁ второй среды (стекла) относительно первой (жидкости): .

Относительный показатель преломления равен отношению абсолютных показателей преломления. Следовательно,

.

Так как угол отражения равен углу падения, то и, следовательно,, откуда

.

Произведём вычисления:

.

Ответ: .

Пример 14 Два николя N₁ и N₂ расположены так, что угол между их плоскостями пропускания составляет . Определить во сколько раз уменьшится интенсивностьI₀ естественного света: 1) при прохождении через один николь N₁; 2) при прохождении через оба николя. Коэффициент поглощения света в николе . Потери на отражение света не учитывать.

Решение. 1) Естественный свет, падая на грань призмы Николя N₁ (рисунок 8), расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный (o) и необыкновенный (e). Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскость чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок света (o) вследствие полного отражения от границы AB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необыкновенный пучок (e) проходит через призму, уменьшая свою интенсивность в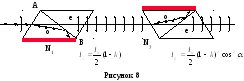следствие поглощения. Таким образом, интенсивность света, прошедшего через первую призму, будет равна

.

Относительное уменьшение интенсивности света получим, разделив интенсивность I₀ естественного света, падающего на первый николь, на интенсивность I₁ поляризованного света:

.

Произведём вычисления:

.

Таким образом, интенсивность уменьшается в 2,1 раза.

2) Плоскополяризованный пучок света падает на второй николь N₂ и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью поглощается призмой, поэтому интенсивность его нас не интересует. Интенсивность I₂ необыкновенного пучка, вышедшего из призмы N₂, определяется законом Малюса (без учёта поглощения света во втором николе):

,

где  – угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

.

Искомое уменьшение интенсивности при прохождении света через оба николя найдём, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей:

.

Заменяя отношение I₀/I₁ его выражением по формуле , получаем

.

Произведём вычисления:

.

Таким образом, после прохождения света через два николя интенсивность его уменьшается в 8,86 раза.

Ответ: 1) ; 2) .

Пример 15 Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластину, интенсивность I пучка света после поляроида стала равна половине интенсивности пучка, падающего на поляроид. Определить минимальную толщину кварцевой пластины. Поглощением и отражением света поляроидом пренебречь, постоянную вращения кварца принять равной .

Решение. Полное гашение света поляроидом означает, что плоскость пропускания поляроида (пунктирная линия на рисунке 9) перпендикулярна плоскости колебаний (I–I) плоскополяризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний на угол

,

где d – толщина пластины.

З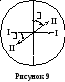ная, во сколько раз уменьшится интенсивность света при прохождении его через поляроид, определим угол, который установится между плоскостью пропускания поляроида и новым направлением (II–II) плоскости колебаний падающего на поляроид плоскополяризованного света. Для этого воспользуемся законом Малюса:

.

Заметив, что , можно записать

.

Из равенства с учётом получим , откуда искомая толщина пластины

.

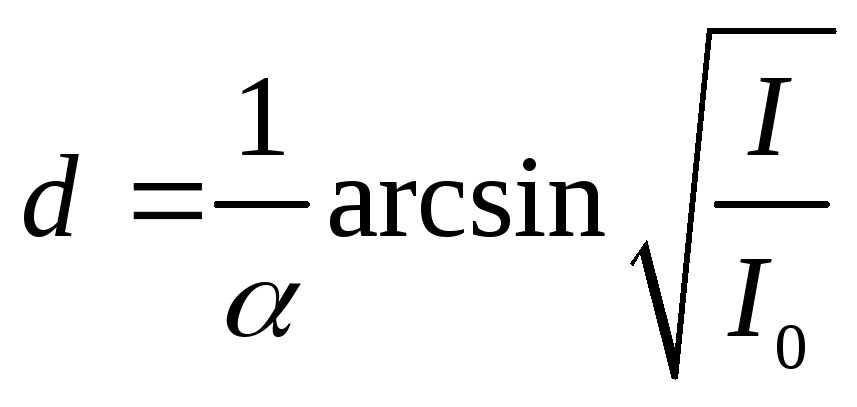Произведём вычисления во внесистемных единицах:

.

Ответ: .

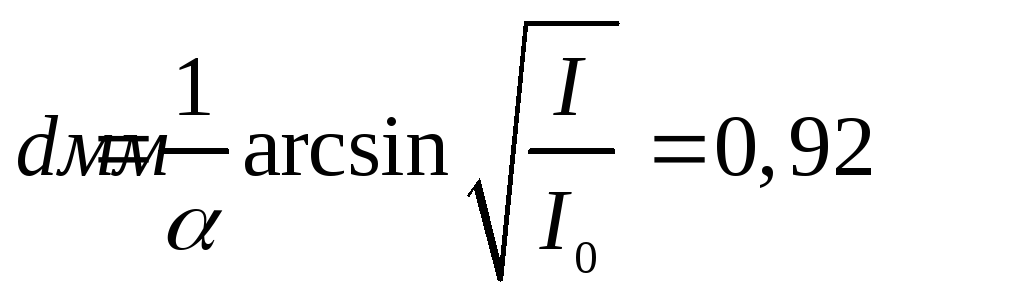Пример 16 Электрон в атоме водорода перешёл с четвёртого уровня на второй. Определить энергию испущенного при этом фотона.

Решение. Для определения энергии фотона воспользуемся одной из сериальных формул Бальмера для водородоподобных ионов:

,

где _mn – длина волны фотона;

R – постоянная Ридберга;

Z – заряд ядра в относительных единицах (при формула переходит в сериальную формулу водорода);

m – номер орбиты, с которой перешёл электрон (n и m – главные квантовые числа).

Энергия фотона выражается формулой

.

Поэтому, умножив обе части равенства на hc, получим выражение для энергии фотона

.

Так как Rhc есть энергия ионизации E_H атома водорода, то

.

Вычисления выполним во внесистемных единицах:

(Приложение В, таблица В12); ;;.

.

Ответ: .

Пример 17 Электрон, начальной скоростью которого можно пренебречь, прошёл ускоряющую разность потенци-алов U. Найти длину волны де Бройля  электрона для двух случаев: 1) ; 2).

Решение. Длина волны де Бройля для частицы зависит от её импульса и определяется формулой

где h – постоянная Планка.

Импульс частицы можно определить, если известна её кинетическая энергия T. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия много меньше её энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).

В нерелятивистском случае

,

где m₀ – масса покоя частицы.

В релятивистском случае

,

где – энергия покоя частицы.

Формула с учётом соотношений и запишется:

в нерелятивистском случае

,

и в релятивистском случае

.

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов ис энергией покоя электрона и в зависимости от этого решим, какую из формул или следует применить для вычисления волны де Бройля.

Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна

.

В первом случае , что много меньше энергии покоя электрона. Следовательно, в этом случае можно применить формулу . Для упрощения расчётов заметим, что. Подставив это выражение в формулу , перепишем её в виде

,

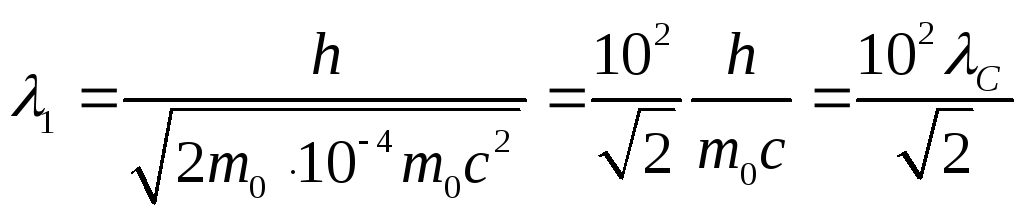где – комптоновская длина волны электрона

Таким образом,

.

Во втором случае , т.е. кинетическая энергия равна энергии покоя электрона. Здесь необходимо применить релятивистскую формулу . Учитывая, что, находим

.

Подставим значение _C и произведём вычисления:

.

Ответ: 1) ; 2).

Пример 18 Кинетическая энергия электрона в атоме водорода составляет величину порядка . Используя соотношение неопределённостей, оценить минимальные линейные размеры атома.

Решение. Соотношение неопределённостей для координаты и импульса имеет вид

,

где x – неопределённость координаты частицы (в данном случае электрона);

p – неопределённость импульса частицы (электрона);

ћ – постоянная Планка h, делённая на 2.

Из соотношения неопределённостей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределённым становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры d, тогда электрон атома будет находиться где-то в пределах области с неопределённостью

.

Соотношение неопределённостей можно записать в этом случае в виде

,

Откуда

.

Физически разумная неопределённость импульса p во всяком случае не должна превышать значения самого импульса, т.е. . Импульсp связан с кинетической энергией T соотношением . Заменимp значением (такая замена не увеличитd). Переходя от неравенства к равенству получим

Произведём вычисления:

.

Ответ: .

Пример 19 Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике ширинойl. Вычислить вероятность нахождения частицы в малом интервале в двух случаях: 1) вблизи стенки (); 2) в средней части ящика ().

Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до ), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние:

.

Графики зависимости волновой функции (x) и плотности вероятности w(x) изображены на рисунке 10. В первом случае искомая вероятность найдётся интегрированием в пределах от 0 до :

.

Знак модуля опущен, так как в данном случае функция (x) является вещественной.

Так как x изменяется в интервале , и следовательно,, справедливо приближённое равенство

.

С учётом этого выражение примет вид

.

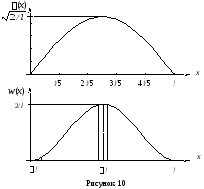
Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи её максимума в заданном малом интервале практически не изменяется. Искомая вероятность во втором случае определяется выражением

,

или

.

Ответ: 1) ; 2).

Пример 20 Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно чёрного тела, равна . Определить энергетическую светимостьR поверхности тела.

Решение. Энергетическая светимость R абсолютно чёрного тела в соответствии с законом Стефана-Больцмана пропорциональна четвёртой степени термодинамической температуры и выражается формулой

где  – постоянная Стефана-Больцмана;

T– термодинамическая температура.

Температуру T можно выразить с помощью закона смещения Вина:

,

где b – постоянная Вина.

Используя формулы и , получаем

.

Произведём вычисления:

.

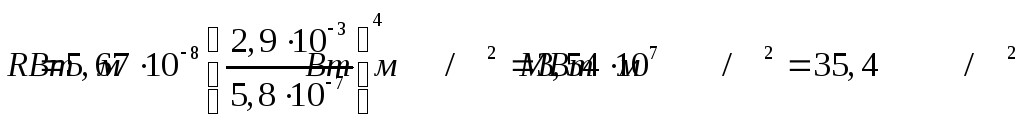Ответ: .

Пример 21 Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны; 2)-излучением с длиной волны .

Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:

,

где – энергия фотонов, падающих на поверхность металла;

A_вых – работа выхода;

T_max – максимальная кинетическая энергия фотоэлектронов.

Энергия фотонов вычисляется также по формуле

,

где h – постоянная Планка;

c– скорость света в вакууме;

 – длина волны фотона.

Кинетическая энергия электрона может быть выражена или по классической формуле

,

или по релятивистской формуле

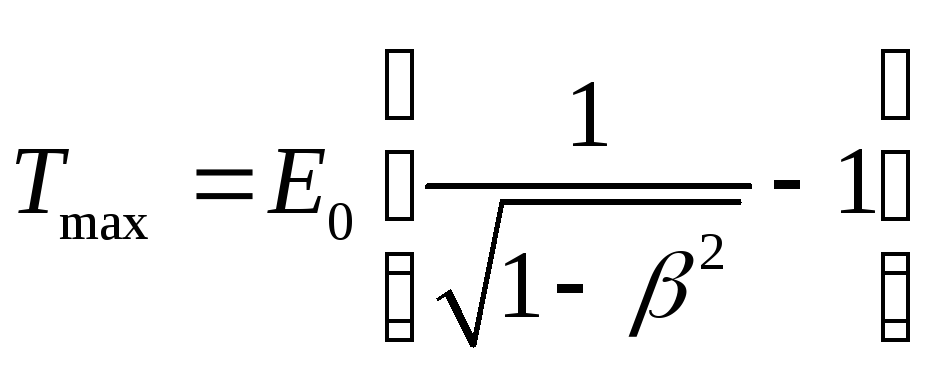
в зависимости от того, какая скорость сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона много меньше энергии покояэлектрона, то может быть применена формула , если жесравнима по величине сE₀, то вычисление по формуле приводит к ошибке, поэтому нужно пользоваться формулой .

1) Вычислим энергию фотона ультрафиолетового излучения по формуле :

.

Полученная энергия фотона (8 эВ) значительно меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле может быть выражена по классической формуле :

,

откуда

.

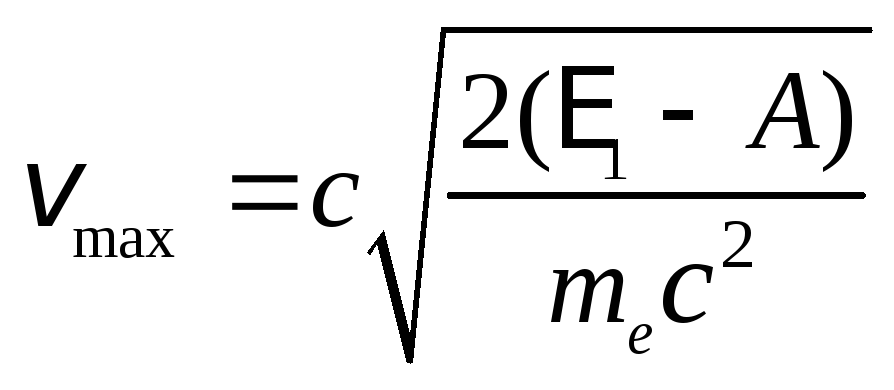Подставив значения величин в формулу и учтя, что работа выхода для серебра равна , найдём

.

2) Вычислим энергию фотона -излучения:

.

Работа выхода электрона () пренебрежимо мала по сравнению с энергией фотона (), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона:. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу для кинетической энергии . Из этой формулы найдём

.

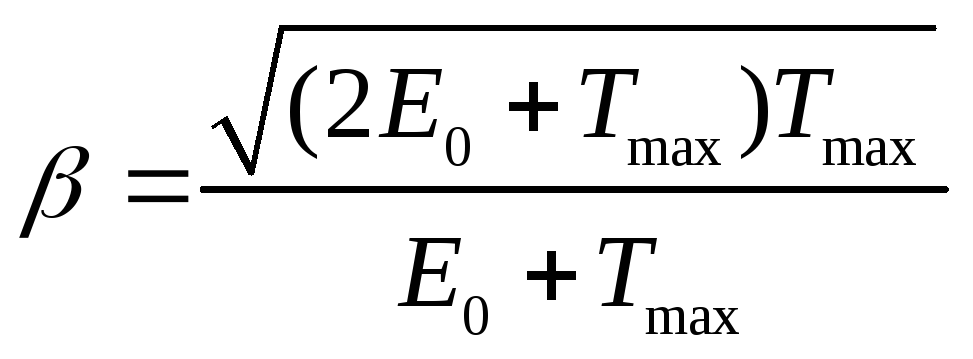Заметив, что и, получим

.

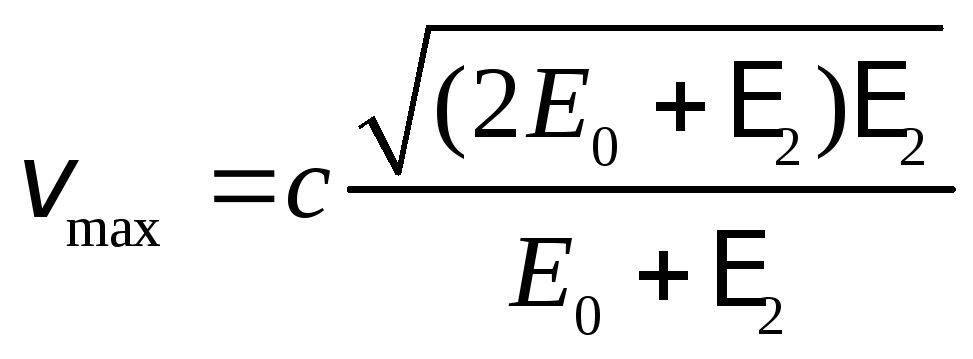Произведём вычисления:

.

Ответ: 1) ;

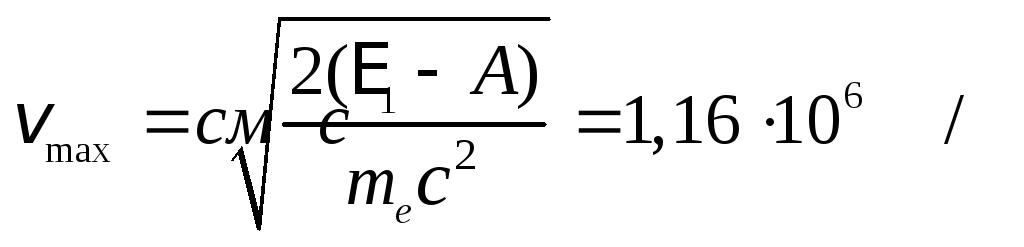2) .

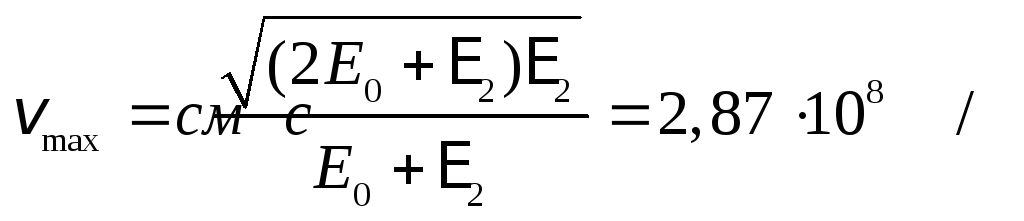Пример 22 В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол . Энергия рассеянного фотона . Определить энергию фотона₁ до рассеяния.

Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона:

,

где – изменение длины волны фотона в результате рассеяния на свободном электроне;

h– постоянная Планка;

m_e – масса покоя электрона;

c– скорость света в вакууме;

 – угол рассеяния фотона.

Преобразуем формулу , выразив в ней длины волн ₁ и ₂ через энергии ₁ и ₂ соответствующих фотонов, воспользовавшись формулой , и умножив числитель и знаменатель правой части формулы наc. Тогда

.

Сокращая на hc и выражая из этой формулы искомую энергию, находим

,

где E₀ – энергия покоя электрона и учтено, что .

Вычисления по формуле удобнее вести во внесистемных единицах. Так как для электрона , то

.

Ответ: .

Пример 23 Пучок монохроматического света с длиной волны падает нормально на плоскую зеркальную поверхность. Поток излучения. Определить: 1) силу давленияF, испытываемую этой поверхностью; 2) число фотонов n, ежесекундно падающих на поверхность.

Решение. 1) Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности:

.

Световое давление может быть найдено по формуле

где E_э – энергетическая освещённость поверхности;

c– скорость света в вакууме;

 – коэффициент отражения.

Подставляя правую часть выражения в формулу , получаем

.

Поскольку представляет собой поток излученияP, то

.

Произведём вычисления, учитывая, что для зеркальной поверхности :

.

2) Произведение энергии  одного фотона на число фотонов n, ежесекундно падающих на поверхность, равно мощности излучения, т.е. потоку излучения:

,

а так как энергия фотона , то

,

откуда

.

Произведём вычисления:

.

Ответ: 1) ; 2).

Пример 24 Узкий монохроматический пучок гамма-лучей падает на поверхность воды. Определить, на какой глубине х (см) интенсивность пучка уменьшится в 20 раз. Длина волны γ-лучей λ = 0,887 пм.

Дано: λ = 0,887 пм =;k=20. Найти: х.

РЕШЕНИЕ: Для решения всех задач на гамма-излучение необходимо пользоваться графиками зависимости коэффициента линейного ослабления μ от энергии Е (см. в конце пособия).

Ослабление интенсивности γ-лучей в веществе происходит по закону Бугера:

, (1)

где - интенсивность падающего пучка,J – интенсивность пучка, прошедшего слой толщиной x, μ – коэффициент линейного ослабления.

По условию задачи . Из уравнения (1) следует, тогда(2).

Логарифмируя (2), получим . (3)

Линейный коэффициент ослабления зависит от энергии падающего излучения, поэтому для определения μ вычислим энергию γ- квантов.

,

где h- постоянная Планка, с – скорость света. Подставляя числовые значения, получаем

По графику зависимости линейного коэффициента ослабления от энергии для воды (стр. 62) определяем μ=0,06 см^-1. Подставляя числовые значения в формулу (3), находим

Ответ : х=50 см.

Пример 25 Период полураспада радиоактивного изотопа T= 5,3 года. Определите: 1) сколько ядер N₁ в массе m = 1,0 г распадется в течение одного года, 2) какая доля (%) нераспавшихся ядер останется

Дано:T=5,3 года, m=10^-3 кг, t = 1,0 год.

Найти: %

РЕШЕНИЕ. Начальное число атомов N₀, содержащихся в 1 г изотопа определяется соотношением

, (1)

где N_A – постоянная Авогадро, ν -число молей, М –молярная масса

Число ядер радиоактивного изотопа N уменьшается с течением времени по экспоненциальному закону

. (2)

Постоянная радиоактивного распада λ связана с периодом полураспада Т соотношением

(3)

Определим количество распавшихся ядер в течение года

(4).

Подставляя формулы (1),(2),(3) в выражение (4), получаем

(5)

Проведем вычисления

Для ответа на второй вопрос надо вычислить по формуле (1) начальное число радиоактивных атомов

.

Тогда

Ответы: