22.Модель множественной регрессии. Интерпретация уравнения регрессии

При решении задач экономического анализа и прогнозирования часто надо определить влияние на показатель Y значений более чем одного связанных с ним показателей (факторов) Х₁, Х₂, …, Х_n, наблюдаемых в разные моменты времени t.

Если между показателями Y и X_i нет функциональной зависимости, то рассматривают стохастическую модель вида

Y = F(Х₁, Х₂…X_р) + U _t, (5.30)

где переменная Y называется зависимой (эндогенной) переменной, Х₁, …, Х_р – независимые (экзогенные) переменные (факторы), F – некоторая функция, U_t случайная величина (характеризует влияние неучтенных факторов), t – момент (период) наблюдения. Как и в случае простой регрессии U _t обычно считается нормально распределенной случайной величиной с математическим ожиданием равным нулю M(U_t) = 0, постоянной дисперсией D(U_t) = const и ковариацией cov(U_t, U_{t + s}) = 0, s > 0.

Функция F называется функцией множественной (многофакторной)

регрессии, а уравнение

_∧

^{Y = F(X}₁ ^{, X}₂ ^{,..., X}_k ⁾

(5.31

уравнением или моделью множественной регрессии, k – количество факторов.

Если функция F – нелинейная функция, то регрессия называется нелинейной, иначе – линейной. Уравнение множественной линейной

регрессией имеет вид:

^∧

^{y = a0 + a1 X 1 + a2 X 2 + ... + ak X k . (5.32)}

^{Коэффициенты (а}_i^{, i = 1 – k) называются коэффициентами}

множественной регрессии.

Основная задача теории линейных регрессионных моделей заключается в определении коэффициентов {а_i, i = 1 – k} по наблюдаемым значениям переменных (Y(t), X₁(t), …, X_k(t)) в различные моменты времени t = 1, 2, …, n, где n – количество наблюдений вектора (Y, X₁, …, X_k).

^{Для определения коэффициентов (а}_i^{, i = 0 – k) запишем уравнение (5.32)}

для различных моментов времени наблюдений (t = 1, 2, …, n). Получим

^{систему n уравнений относительно k – неизвестных (а}_i^{, i = 0 – k),}

предполагается, что k < n:

^∧

t t t t

^{y = a0 + a1 x1 + a2 x2 + ... + ak xk ,}

^(5.33)

_{t = 1,2,..., n.}

Систему уравнений (5.34) можно записать в матричном виде:

^∧

^{Y = Xа, (5.34)}

где а = (а₀…а_k)^Т – неизвестный вектор параметров модели (5.32);

^{Х – матрица наблюдаемых значений факторов Х}_i^:

_{1 1 1}

_{⎡1 x1}

_{x2 ... xk ⎤}

_{⎢ 2 2 2 ⎥}

_{X = ⎢}^{1 x}₁

^x₂ ^{... x}_{k ⎥ . (5.35)}

_{⎢.................... ⎥}

^⎢

_{⎢⎣1 x} ⁿ

^⎥

_x ⁿ _{... x} ⁿ _⎥⎦

1 2 k

_{Система уравнений (5.34) имеет n уравнений и (к + 1) неизвестных}

^{а = (а}₀^…а_k^)Т.

В стандартном регрессионном анализе предполагается, что k < n и

i

rang(X) = k.

Как и в простой линейной регрессии, для определения вектора неизвестных параметров а = (а₀, …, а_k)^Т модели (5.32) по результатам наблюдений используется метод наименьших квадратов (МНК).

Построим вектор наблюдаемых значений показателя Y:

Y = (y^t_., y², …, yⁿ)^T (5.36)

_{и вектор регрессионных значений согласно (5.32):}

_{∧ ∧ ∧ ∧}

_{Y = ( y}¹ _{, y} ² _{,..., y} ⁿ _).

_{∧ ∧ ∧ ∧}

Вектор

_{регрессии.}

^{e = Y − Y = ( y1 − y1 , y 2 − y 2 ,..., y n − y n ) называется вектором остатков}

Параметры (а₀, …, а_k) находятся методом наименьших квадратов (МНК)

из задачи минимизации суммы квадратов остатков:

_∑

Коэффициенты (а_i) выбираются так, чтобы сумма квадратов остатков регрессии была минимальной. Если ввести функцию

L ( a ₀ , a ₁ ,...,

^{a k ) =}

_n

^∑

^{t = 1}

( y ^t

_k

^{− ∑}

^{i = 0}

a _i X _i

i

)

t 2

(5.38)

то задача (5.37) эквивалентна системе уравнений:

^{∂L(a0 , a1 ,..., ak )} _{= 0,}

^∂ai

^{i = 0,1,2,..., k.}

Для обеспечения качества модели необходимо, чтобы было n > 3k, где n – количество наблюдений, k – количество факторов. Модель множественной регрессии оценивается с помощью следующих критериев:

_{1. Коэффициент детерминации (R}²_):

^{Всегда 0 < R2 < 1. Чем ближе R2 к 1, тем точнее модель. Если R2 > 0,8, то}

модель считается точной, если R² < 0,5, то модель надо улучшить, либо выбрав другие факторы, либо увеличив количество наблюдений.

_{2. Коэффициент множественной корреляции:}

_{R = R} ² _{. (5.44)}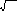

_{3. Скорректированный коэффициент детерминации:}

^{R 2 = 1 − (1 − R 2 )}

c

^{4. Стандартная ошибка:}

^{n − 1}

^{n − k − 1}

. (5.45)

_n

_∑ ^(Y_t

^∧

^{− Y t ) 2}

^{SE =}

^{t =1 . (5.46)}

^{n − k − 1}

5. Оценка значимости модели, т.е. оценка того насколько верна гипотеза о линейности регрессии между Y и факторами X_i осуществляется по F-критерию Фишера. По наблюдаемым значениям определяется значение

_{F =} ^R

2

^{(n − k − 1)} _{. (5.47)}

набл

_{(1 − R} ² _)k

Если F_набл > F_кр = F_табл(0,95; n – 1; n – k – 1), где 0,95 – уровень доверительной вероятности, (n – 1) и (n – k – 1) степени свободы модели, то модель считается значимой, и принимается гипотеза о линейной регрессии между переменными Y и X_i, где F_табл – табличное значение F-критерия Фишера.

Иначе гипотеза о линейной регрессии отвергается и надо изменять модель: выбрать другие факторы, увеличить количество наблюдений или построить нелинейную регрессию.

6. Оценка значимости коэффициентов регрессии (кроме свободного члена) осуществляется сравнением статистики

_{a j}

_{t j = (5.48)}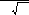

^{SE b} _jj

с табличным значением t-статистики Стьюдента. В (5.48) b_jj – диагональный элемент матрицы (Х^ТХ)^–1. Если значение (5.48) превосходит табличное значение t-статистики Стьюдента, то j-й коэффициент считается значимым, в

противном случае фактор, соответствующий данному коэффициенту следует исключить из модели.

7. Доверительный интервал для прогнозных значений линии регрессии определяется по формуле

_{∧ ∧}

^{(Y t − V}_t ^{, Y t + V}_t ^),

п

п

(5.49)

где

^V_t ^{= SE ⋅ t(α , n − k − 1)}

^{x T (t )( X T X ) −1 x}

(t ) , (5.50)

_{t (a, n − k − 1) −}

_{табличное значение критерия Стьюдента при заданном}

^{уровне значимости α и числе степеней свободы (n – k – 1);}

^{хп(t) – вектор-столбец факторов для прогнозных значений времени}

_{(t = n + 1, n + 2, n + 3, …).}

_{Матрица (Х}^Т_Х)^–1 _{соответствует наблюдаемым значениям факторов.}

8. Влияние факторов Х на показатель Y оценивается с помощью коэффициентов эластичности Э_j и бета-коэффициентов:

Коэффициенты эластичности Э_j показывают, на сколько процентов изменится значение переменной Y при изменении Х_j на 1%. Бета коэффициенты показывают, на какую часть среднеквадратичного

отклонения изменится Y при изменении Х_j на величину своего среднеквадратичного отклонения.

Долю влияния j-го фактора в суммарном влиянии всех факторов на показатель Y оценивают с помощью дельта-коэффициентов^r_yj ^{– коэффициент корреляции между j-м фактором и переменной Y.}

При k = 1 получаются оценки для модели простой (однофакторной)

регрессии.