Овчаренко_8

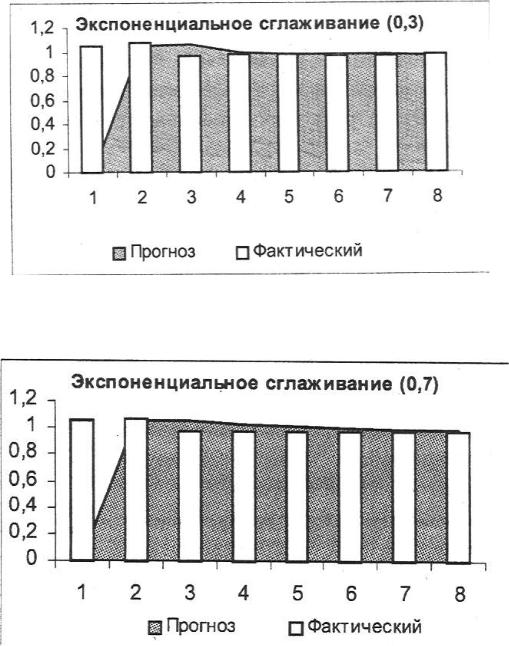
предыдущего сглаженного значения (для первого значения оно отсутствует). Ошибка прогнозного значения в текущей ячейке рассчитывается исходя из значений, находящихся в трех предыдущих ячейках. Данный метод позволяет делать прогноз на 1 шаг вперед. В выходной таблице самое последнее значение является прогнозным значением на следующий период. Точность прогноза повышается при росте размера входного интервала (не

менее 30).

Ниже приведены графики, построенные для различных коэффициентов экспоненциального сглаживания (рис. 6.9 и рис. 6.10):

Рис. 6.9. Экспоненциальное сглаживание курса ценных бумаг, коэффициент затухания 0,3.

Рис. 6.10. Экспоненциальное сглаживание курса ценных бумаг, коэффициент затухания 0,7.

6.5. Регрессионный анализ

Связи между различными величинами носят функциональный или

корреляционный характер. Функциональная зависимость означает детерминированную, предопределенную заранее связь между величинами и может быть выражена точным математическим соотношением. Корреляционная зависимость означает стохастическую (случайную) связь между величинами и в общем случае выражается ковариацией или коэффициентом корреляции, при этом одна независимая случайная величина рассматривается как фактор, а другая случайная величина — как основной признак, для которого оценивается мера тесноты связи с фактором.

Форма взаимосвязи случайных величин и функции получила название уравнения регрессии. Различают простую (парную) и множественную регрессию линейного и криволинейного (квадратичного, экспоненциального, полулогарифмического и т.д.) типа. Вид и параметры уравнения регрессии устанавливаются с помощью метода наименьших квадратов отклонений эмпирических данных от выровненных.

Статистическая оценка тесноты связи основана на показателях вариации:

•общая дисперсия результативного признака, обусловленная влиянием всех факторов в совокупности —σ2у;

•факторная дисперсия результативного признака, отражающая вариацию результативного признака от воздействия фактора — σ2уx;

•остаточная дисперсия результативного признака, отражающая

вариацию результативного признака от воздействия всех прочих факторов, кроме выделенного — σ2s.

	σ2y =	∑( yi − y)	;	σ2yX	=	∑( y xi − y)	; σ2Si	=	∑( yi − ySi )	;
						n			n
		n

Основное соотношение: σ2y = σ2yX +σ2S .

Качественная оценка степени связи случайных переменных — коэффициент детерминации, который вычисляется как отношение факторной к общей дисперсии — R2, доля факторной дисперсии в общей дисперсии. Иногда используется индекс корреляции — R. Для оценки значимости R применяется F-критерий Фишера:

FX =			R2			n −m	,
	1		− R	2		m −1

где п — число объектов анализа (размер выборки); т — число параметров уравнения регрессии (факторов).

Фактическая величина критерия сравнивается с критическим значением, определяемым с учетом уровня значимости и числа степеней свободы: k1 = т — 1; k2 = п — т.. Если фактическое значение больше критического, величина R признается существенной.

Качественная оценка степени связи случайных переменных может быть выявлена на основе оценки коэффициента детерминации по шкале Чеддока:

	Коэффициент	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
	детерминации
	Характеристика	слабая	умеренная	заметная	высокая	весьма
	силы связи					высокая

При значениях коэффициента детерминации более 0,7 вариации зависимой переменной, в основном, обусловлены влиянием факторов, и регрессионные модели признаются пригодными для их практического использования в целях прогнозирования

Найденные коэффициенты уравнения регрессии являются оценками истинных значений параметров Если анализируется совокупность малого размера (до 30 значений), то для определения доверительного интервала параметров используют распределение Стьюдента (значение t-критерия Стьюдента). Данный критерий определяет число элементов анализа и среднеквадратические отклонения

•результативного признака от выровненных значений по модели,

•факторного признака от общей средней.

Например, для парной линейной корреляции, имеющей уравнение модели

yx = a0 +a1 x,

вычисляются фактические значений t-критерия для каждого коэффициента:

t	a	= a	0	n −2	,	t	a	= a	n −2 σ	x	,
				σS				1	σS
		0					1

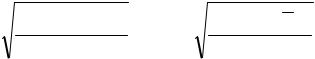
	σS =	∑( y1 − yx )2	, σx =	∑(x1 − x)2
		n		n

Приняты следующие обозначения: yi — значение результативного признака;

yxi — выровненное значение результативного признака (модельное

значение);

xi — значение факторного признака;

x — общая средняя факторного признака.

Рассчитанные значения t-критериев сравниваются с критическими с учетом принятого уровня значимости и числа степеней свободы и признаются типичными, если фактическое значение больше критического.

Если анализируется совокупность достаточно большого размера, вместо таблицы распределения Стьюдента пользуются таблицей интеграла вероятностей Лапласа.

6.5.1. Информационная технология линейной регрессии в Пакете анализа.

При выполнении команды Сервис, Анализ данных выбирается режим Регрессия, появляется одноименное диалоговое окно (рис. 6.11).

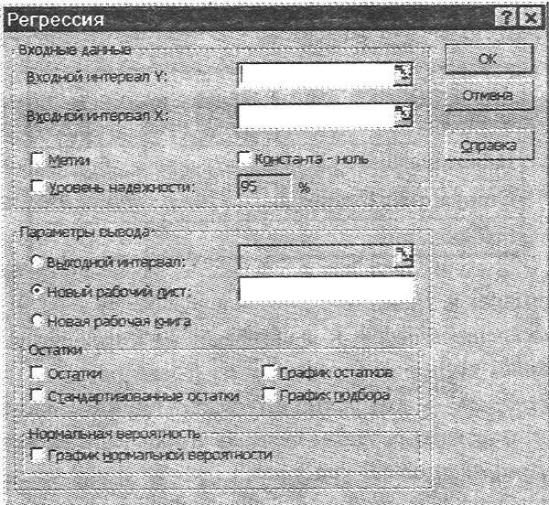
Рис. 6.11. Диалоговое окно режима Регрессия.

В данном окне задаются:

Входной интервал Y — интервал результативного признака (зависимых данных), подлежащих анализу. Зависимые данные должны быть введены в

отдельном столбце;

Входной интервал Х — интервал факторов (независимых данных),

подлежащих анализу. Независимые переменные упорядочены слева направо с использованием индексов 1, 2, 3 и т.д. в выходной таблице (максимальное число входных интервалов равно 16);

Константа ноль —линия регрессии проходи) через начало координат;

Уровень надежности — по умолчанию 95%;

Выходной интервал — верхняя левая ячейка интервала, в который выводятся выходные таблицы (не менее семи столбцов для итоговой выходной таблицы).

Результаты регрессионного анализа размещаются в трех таблицах. Например, проведение регрессионного анализа для курса акций во взаимосвязи с номиналом, эмиссией и спросом на ценные бумаги (см. пример выше) дает следующие результаты:

1. Регрессионная статистика — оценка корреляционной связи:

Регрессионная статистика

Множественный R	0,922
R-квадрат	0,850
Нормированный R- квадрат	0,738
Стандартная ошибка	0,020
Наблюдения	8

Пояснения к таблице:

•Множественный R — коэффициент корреляции Пирсона, равный корню квадратному из R-квадрат;

•R-квадрат — коэффициент детерминации, характеризует тесноту связи результативного и факторных признаков;

•Нормированный R-квадрат;

•Стандартная ошибка — среднеквадратическое значение отклонения

регрессии от эмпирических данных;

•Наблюдения — количество (п) наблюдений в массиве.

2.Таблица дисперсионного анализа — ANOVA:

Дисперсионный анализ	df	ss	MS	F	Значимость
Регрессия	3	0,0095	0,0032	7,582	0,0398
Остаток	4	0,0017	0,0004
Итого	7	0,0111

Пояснения к таблице:

• df — число степеней свободы; для строки Регрессия это число переменных (рассматриваемых факторов) в уравнении регрессии — в данном случае 3 (номинал, эмиссия и спрос на ценные бумаги); для строки Остаток

— размер выборки минус число параметров в регрессии минус 1; для строки Итого — размер выборки минус 1.

• SS — сумма квадратов отклонений для расчета дисперсии:

для строки Регрессия — факторной, для строки Остаток — остаточной, для строки Итого — общей;

• MS — дисперсия, рассчитываемая как отношение суммы квадратов отклонений к величине df;

• F — статистика для оценки связи между зависимой и независимыми переменными, определяется как:

MS( Регрессия )/MS( Остатки),

• Значимость F — значение уровня значимости αF , соответствующее вычисленному значению Fr .

В рассмотренном примере модель регрессии правомерна:

вычисленная по формуле вероятность правильного прогноза близка к 1:

Р = 1 — 0,0398 = 0,9602;

если уровень значимости αF =0,05, то и в этом случае будет соблюдено требование Fr > Fk , т.к. по таблицам Фишера Fk =5,82, a вычисленное

значение 7,582.

3. Таблица параметров модели* и их статистических оценок:

		Y-пересечение	Номинал	Эмиссия	Спрос ЦБ
			ЦБ	ЦБ
	Коэффициенты	1,01	0,00	-0,03	0,03
	Стандартная	0,03	0,00	0,01	0,01
	ошибка
	t-Статистика	33,04	1,32	-2,64	2,90
	Р-значение	0,00	0,26	0,06	O.G-r
	Нижние 95%	0,92	0,00	-0,07	0,00
	Верхние 95%	1,09	0,00	0,00	0,07

* Таблица представлена в транспонированном виде.

Пояснения к таблице:

•Коэффициенты — значения параметров модели регрессии;

•Стандартная ошибка — параметров уравнения регрессии;

•t-Статистика — отношение Коэффициент/Стандартная ошибка;

•Р-значение — уровень значимости αc для значений t-Статистики,

•Верхние и Нижние — границы доверительного интервала для коэффициентов уравнения регрессии, вычисляемые при различных уровнях значимости αc .

4.Вывод прогнозных значений по модели и остатков:

Наблю-	Предсказанное	Остатки	Стандартные	Персентиль	Курс ЦБ
дение	Курс ЦБ		остатки
1	1,05	0,00	0,00	6,25	0,97
2	1,05	0,02	1,35	18,75	0,97
3	0,98	-0,01	-0,74	31,25	0,97
4	0,99	-0,01	-0,90	43,75	0,98
5	0,99	-0,01	-0,90	56,25	0,98
6	0,95	0,02	1,05	68,75	0,98
7	0,95	0,02	1,05	81,25	1,05
8	0,99	-0,01	-0,90	93,75	1,07

Пояснения к таблице

• Предсказанное Y — расчетные значения по модели регрессии;

•Остатки — разность эмпирического и предсказанного по модели регрессии значений.

По желанию пользователя могут быть выведены следующие виды графиков:

•График остатков — для каждой независимой переменной обеспечивает отображение остатков как разностей между эмпирическими и регрессионными значениями,

•График подбора — диаграмма для сопоставления предсказанных значений по регрессионной модели с данными наблюдений,

•График нормального распределения — диаграмма для нормальных вероятностей прогнозных значений Автоматически формируется интервал персентилей, для которых указываются соответствующие модели значения Y

6.6. Трендовые модели.

Значение некоторых экономических показателей, имеющих случайный характер, можно интерпретировать в виде временных рядов — эмпирической последовательности данных, полученных в определенные моменты времени ti , где i — порядковый номер значения эмпирического ряда на временной

оси. Каждый такой ряд характеризуется некоторой тенденцией развития процессов во времени, называемой трендом Трендовые модели временных рядов обеспечивают выдачу прогнозов на краткосрочный и среднесрочный периоды при выполнении ряда условий:

—период времени, за который изучается прогнозируемый процесс, должен быть достаточным для выявления закономерностей,

—трендовая модель в анализируемый период должна развиваться эволюционно;

—процесс, описываемый временным рядом, должен обладать определенной инерционностью, т е. для наступления большого изменения в поведении процесса необходимо значительное время;

—автокорреляционная функция временного ряда и его остаточного ряда должна быть быстро затухающей, т е. влияние более поздней информации должно сильнее отражаться на протезируемой оценке, чем влияние более ранней информации.

На практике наиболее распространенными методами статистического изучения тренда являются методы:

•укрупнения интервалов для выявления тренда в колеблющихся временных рядах. Эмпирические ряды преобразуются в ряды большей продолжительности (месячные в квартальные, квартальные в годовые и т.п.)*;

• скользящей средней с заданным периодом (N) осреднения эмпирических данных, вес которых одинаков ( N1 ). Осреднение обеспечивает

устранение случайных колебаний эмпирических данных, выявление основной тенденции развития в виде плавной линии;

• аналитического выравнивания в виде функции тренда f(t),

зависящей от времени.

Линии тренда широко используются для решения задач прогнозирования с помощью методов регрессионного анализа. Подбор функции тренда f(t) осуществляется методом наименьших квадратов, при котором минимизируется сумма квадратов отклонений между эмпирическими значениями и соответствующими значениями функции. Для оценки точности модели используют коэффициент детерминации, построенный на основе оценок дисперсии эмпирических данных и значений трендовой модели. Трендовая модель адекватна эмпирическому процессу и отражает тенденции его развития при значениях коэффициента детерминации, близких к 1.

Наблюдаемые явления во времени развиваются:

1) равномерно при постоянном абсолютном приросте очередного уровня временного ряда. Основная тенденция развития отображается линейным типом тренда:

y) = C0 +C1t,

где C0 — постоянная составляющая;

C1 — коэффициент регрессии, определяющий постоянные скорость и

направление развития:

если с1 > 0, уровни динамики равномерно возрастают; если с1 < 0, уровни динамики равномерно снижаются;

2) равноускоренно при постоянном во времени увеличении (замедлении) темпа прироста уровней. Основная тенденция развития отображается функцией параболы второго порядка:

y) =C0 +C1t +C2t 2 ,

где С0 — постоянная составляющая; С1 — коэффициент, определяющий скорость и направление развития;

С2— коэффициент, характеризующий постоянное изменение скорости (темп) развития:

при С2 > 0 происходит ускорение, при С2 < 0 — замедление роста;

Наиболее удобным инструментом группирования временных рядов является сводная таблица, которая позволяет осуществлять группировку значений по определенным полям, расположенным в области строк или столбцов. Так, если в строке разместить поле типа дата, можно

осуществлять группирование по интервалам: определенное число дней, месяц, квартал, год.

3) с переменным ускорением (замедлением) при переменном во времени увеличении (замедлении) развития. Основная тенденция отображается полиномом степени от 3 до 6, то есть:

y) = c0 +c1t +c2t 2 +c3t3 +c4t 4 +c5t5 +c6t 6 ;

4) с замедлением роста в конце периода, когда прирост в конечных уровнях ряда динамики стремится к нулю. Основная тенденция отображается логарифмической функцией вида:

y) = c0 ln t +c1;

5) для описания простейшего потока однородных событий (t — случайное время появления очередного события) используется

экспоненциальная функция роста:

y) = c0 ect ;

6) при постоянном относительном приросте для выражения обратно пропорциональной зависимости — степенная функция, частный случай — гипербола (с = -1):

y = c0 t c ;	y = c +	c1	.
		t

EXCEL строит трендовые модели графическим способом на основе диаграмм, представляющих уровни динамики. Для эмпирического ряда данных строится диаграмма определенного типа: линейчатая; график; гистограмма; точечная. Диаграмма переводится в режим редактирования, выделяется ряд для построения линии тренда*, выполняется команда меню

Диаграмма, Добавить линию тренда, появляется диалоговое окно для выбора типа линии тренда: линейный, логарифмический, полиномиальный (полином определенной степени), степенной, экспоненциальный, скользящее среднее (для указанного периода сглаживания). На вкладке Параметры указываются параметры тренда:

•Имя тренда — имя линии тренда, располагается в легенде диаграммы; возможны следующие варианты задания имени тренда:

•Автоматическое — линия тренда именуется по выбранному типу

тренда;

•Пользовательское;

•Прогноз — доступен только для регрессий:

•Вперед на — количество периодов, на которое линия тренда проектируется в будущее, т.е. в направлении от оси Y;