физика

Импульс материальной точки

p m .

Импульс системы n материальных точек

n

n

P pi

mi i .

i 1

i 1

Закон изменения импульса системы материальных точек:

dP

n

Fiвнеш .

dt

i 1

n

Если Fi

внеш 0 , то выполняется закон сохранения импульса системы

i 1

материальных точек:

n

n

Pi mi i const .

i 1

i 1

Элементарная работа силы F на бесконечно малом перемещении dr

A (F,dr )

F

dr

cos ,

где – угол между направлением силы

F

и направлением перемещения dr .

Работа силы

F на участке траектории 1 – 2:

2

2

2

2

2

A12 A

( F ,dr )

Fx dx Fy dy Fz dz ,

1

1

1

1

1

где dr dxi dyj

dzk – бесконечно малое перемещение точки.

Мощность силы

N A

(F, dr )

(F, )

F

cos ,

dt

dt

где – угол между направлением силы F

и направлением скорости .

Закон изменения полной механической энергии системы материальных

точек:

E E E Aвнутр

Aвнеш ,

2

1

нкс

нкс

где Aнксвнутр

– работа всех внутренних неконсервативных сил; Aнксвнеш – работа

всех внешних неконсервативных сил, действующих на систему.

Если Aвнеш Авнутр 0 , то выполняется закон сохранения полной

меха-

нкс

нкс

нической энергии:

E T Uвз +Uвнеш = const ,

где E –

полная

механическая энергия

системы

материальных точек;

T –

суммарная кинетическая энергия системы; U вз – потенциальная энергия взаимодействия системы материальных точек между собой; Uвнеш – потенциальная энергия точек системы во внешнем силовом поле.

11

Момент инерции тела относительно некоторой оси

I R2dV ,

(V )

где – плотность тела; dV – элементарный объем; R – расстояние от dV до выбранной оси.

Момент инерции сплошного однородного диска (цилиндра) относительно оси, проходящей через центр диска перпендикулярно его плоскости:

I mR2 , 2

где m – масса диска; R – радиус диска (цилиндра).

Момент инерции однородного шара относительно оси, проходящей через центр шара:

I 25 mR2 ,

где m – масса шара; R – радиус шара.

Момент инерции тонкого стержня относительно оси, проходящей через центр стержня перпендикулярно к нему:

I ml 2 , 12

где m – масса стержня; l – длина стержня.

Модуль момента силы M r , F равен

M rFsin lF ,

где r – модуль радиуса-вектора точки приложения силы; F – модуль силы;– угол между направлением силы и направлением радиуса-вектора точки; l r sin – плечо силы.

Модуль момента импульса L r , p равен

L rpsin lp ,

где p – импульс тела; l r sin – плечо импульса.

Основной закон динамики вращательного движения твердого тела относительно неподвижной оси вращения z :

N

I z Mizвнеш , i 1

где I – момент инерции тела; z – проекция углового ускорения тела на ось z ;

N

Mizвнеш – сумма моментов всех внешних сил, действующих на тело, относи-

i 1

тельно оси z .

N

Если M izвнеш 0, то выполняется закон сохранения момента импульса

i 1

тела относительно оси z :

12

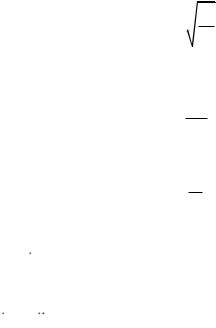
	Lz Iωz		const ,
где z	– проекция угловой скорости тела на ось z ; I – момент инерции тела от-
носительно оси z .
Кинетическая энергия твердого тела при плоском движении
	T	m c2		Ic 2	,
где c	2		2
	– скорость центра масс твердого тела; Ic – момент инерции твердого те-

ла относительно оси, проходящей через его центр масс.

1.2. Механические колебания

Кинематический закон гармонических колебаний материальной точки: x(t) Acos( 0t 0 ) ,

где x – смещение точки от положения равновесия; A – амплитуда колебаний; ( 0t 0 ) – фаза колебаний; 0 – начальная фаза колебаний.

Квазиупругая сила

Fx kx .

Собственная циклическая частота гармонических колебаний под действием квазиупругой силы

0 mk ,

где k – коэффициент квазиупругой силы; m – масса колеблющейся точки. Период гармонических колебаний

T2 .0

Частота колебаний

T1 .

Скорость точки при гармонических колебаниях

x x A 0 sin( 0t 0 ) A 0 cos( 0t 0 2 ) .

Ускорение точки при гармонических колебаниях

ax x x A 02 cos( 0t 0 ) A 02 cos( 0t 0 ) .

Полная механическая энергия материальной точки при гармонических колебаниях

E E	E		m	2		kx2
			x				,
k	n		2			2
где Ek – кинетическая энергия точки; En		– потенциальная энергия точки.

Период малых колебаний математического маятника

13

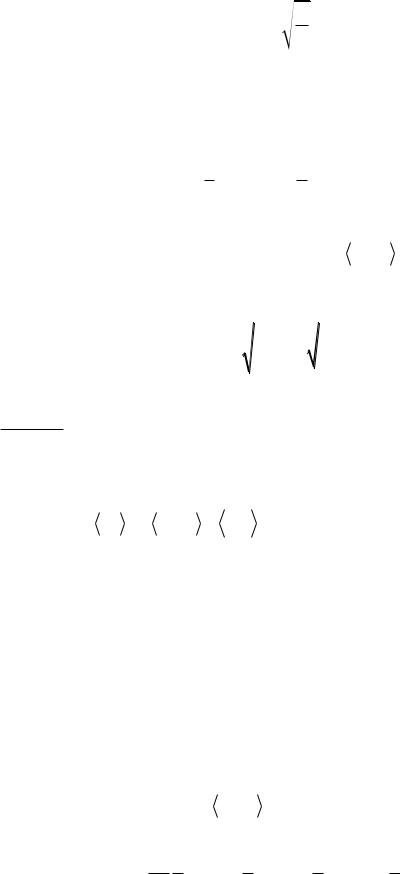
T 2 gl ,

где l – длина математического маятника; g – ускорение свободного падения.

1.3. Молекулярная физика и термодинамика

Основное уравнение молекулярно-кинетической теории идеальных газов:

p 13 nm0 кв2 23 n пост ,

где p – давление газа; n – концентрация молекул; m0 – масса одной молекулы;

кв – среднеквадратичная скорость молекул газа;

пост

m

кв

2

0

– средняя

2

кинетическая энергия поступательного движения одной молекулы.

Среднеквадратичная скорость молекулы газа

кв

3kT

3RT

,

m0

M

где k 1,38 10 23 ДжК – постоянная Больцмана; T – абсолютная температура;

R 8,3	Дж	– универсальная газовая постоянная; M – молярная масса газа.
	моль К

Средняя кинетическая энергия жесткой молекулы газа, имеющей i степеней свободы,

i

i

iвр

k

пост

вр

kT

пост

kT

kT ,

2

2

2

где i – число степеней свободы жесткой молекулы; iпост – число поступательных степеней свободы; iвр – число вращательных степеней свободы.

Для одноатомной молекулы

i iпост 3

Для двухатомной жесткой молекулы

i iпост iвр 3 2 5.

Для трехатомной жесткой молекулы

i iпост iвр 3 3 6.

Кинетическая энергия поступательного движения всех молекул газа массой m

	N			Nm	2		m	2
E		пост		0 кв				кв	.
пост				2			2

Внутренняя энергия идеального газа массой m

U Mm 2i RT 2i RT 2i kN AT 2i pV ,

14

	где	m		N	– число молей газа (количество вещества); N – число молекул,
		M		N A
	содержащихся в газе массой m ; NA 6,02 1023					моль 1 – число Авагадро.

Уравнение состояния идеального газа:

pV Mm RT ,

где p – давление; V – объем; T – температура газа.

Работа сил давления газа при изменении его объема:

V2

A12 pdV ,

V1

где V1 – начальный объем газа; V2 – конечный объем газа; p – давление газа.

Первое начало термодинамики:

Q U A,

где Q – количество теплоты, полученное системой (газом); U – изменение внутренней энергии системы; А – работа, совершенная силами давления системы.

Молярная теплоемкость газа при V = const:

CV 2i R .

Молярная теплоемкость газа при p = const:

C i 2 R .

p 2

Уравнение Майера:

Cp СV R .

Уравнение адиабатического процесса:

pV const ,

где Cp i 2 – показатель адиабаты.

CV i

Коэффициент полезного действия (КПД) тепловой машины:

	A		Q1 Q2	1			Q2			,
	Q1		Q1				Q1

где А – работа, совершенная газом за цикл A 0 ; Q1 – количество теплоты,

полученное рабочим веществом (газом, паром) тепловой машины от нагревателя Q1 0 ; Q2 – количество теплоты, переданное рабочим веществом холо-

дильнику (окружающей среде) Q2 0 .

Коэффициент полезного действия (КПД) цикла Карно:

Q1 Q2 T1 T2 ,

Q2 T1

где T1 – температура нагревателя; T2 – температура холодильника.

15

1.4. Примеры решения задач

Пример 1.1. Радиус-вектор точки A относительно начала координат меняется по закону r t ti bt2 j , где , b – постоянные, i , j – орты осей x и y . Найти: а) уравнение траектории точки y x ; изобразить ее гра-

фик; б) зависимость от времени вектора , ускорения a и модулей этих величин; в) зависимость от времени угла между векторами a и .

Дано:

r t ti bt2 j

, const 0

y x ?, t ?, a t ? , t ? ,

a t ?, t ?

Решение. В задаче задан закон движения материальной точки

	r t ti bt2 j ,			(1)
где t x t ;	bt2 y t . Найдем t из			x t ,
t x . Подставим его в y t bt2 , получим
	y x	b	x2 .	(2)
		2

Это есть уравнение параболы.

y

a

y

A x

x

Рис.1.1

Нарисуем ее график. Точка A движется по параболе. Вектор скорости точки A направлен по касательной к траектории. Разложим его на составляющие x

и y :

xi

y j .

Найдем

t

и

t ,

используя

уравнение (1):

t

dr t

dx

i

dy

j

i

j

x

y

(3)

dt

dt

dt

i 2btj,

t x2

2y

2

4b2t2 .

(4)

Найдем

a t и a t , используя уравнение (3):

a t

d t

d x

i

d y

j 2bj .

(5)

dt

dt

dt

a

t 2b .

(6)

Как видно из (5), a t направлено по оси y . Из рис. 1.1 видно, что угол

между и

a можно найти через x

и y :

x

tg

.

(7)

y

2bt

16

Отсюда t arctg 2bt .

Ответ: y x b2 x2 ; t i 2btj ; t 2 4b2t2 ;

a t 2bj ;	a t 2b ;	t arctg			.
			2bt
Пример 1.2. Частица движется в положительном направлении оси				X

так, что ее скорость меняется по закону x , где – положительная постоянная. В момент времени t 0 частица находится в точке x 0 . Найти: а) зависимость от времени скорости и ускорения частицы; б) среднюю скорость частицы за время, в течение которого она пройдет первые s метров пути.

Дано:

x , s

При t 0 x 0

const 0

t ? , a t ?,

?

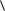Решение. Модуль скорости частицы, движущейся вдоль оси x, есть первая производная от координаты по времени:

	dx	.	(1)
	dt

По условию задачи скорость частицы меняется по закону

x .			(2)

Приравняем (1) и (2), получим

dx

x .

(3)

dt

Разделим переменные в (3) и, проинтегрировав

x

t

dx

dt,

0

x

0

получим 2 x = t .

Следовательно,

x t

2t2 .

(4)

4

Скорость частицы как функцию t

найдем по формуле (2):

t

2t

.

(5)

2

Ускорение частицы есть первая производная от скорости по времени и

с учетом (5):

a(t)

d (t)

2 .

(6)

dt

2

17

Как видно из (6), a const .

Средняя скорость частицы определяется по формуле

1

t2

(t)dt .

(7)

t

t

2

1 t

1

Для нашей задачи t 0 , а

t

2

это время,

за которое частица пройдет

1

первые s метров пути. Определим это время из (4): t

4x

, заменив в фор-

2

муле x s , получим

t

4s

.

(8)

2

2

С учетом (5)

найдем среднюю скорость частицы

:

1 t2

2t

1 2t2

2t

4 2

2

,

t

2

t

4

2

0

2

или с учетом (8)

2

4s

s

.

(9)

4

2

2

Ответ:

(t)

2t

; a(t) 2 ;

s .

4

2

2

Пример 1.3.

Колесо

радиусом

R 0,1

м

вращается

по

закону

t a bt ct 3,

где b 3

рад/с и c 2 рад/с 3 . Для точек, лежащих на обо-

де колеса, найти через 3 с

после

начала

движения

следующие

величины:

1) угловую скорость, 2) угловое ускорение, 3) линейную скорость, 4) тангенциальное ускорение, 5) нормальное ускорение.

Дано:

R 0,1 м

t a bt ct 3

b3 рад/с

c2 рад/с 3

t3 с

t0 0 с

? , ? t ? , a t ? , an t ?

Решение. Задан кинематический закон движения любой точки на ободе колеса (угловой путь, проходимый точкой за время t ):

t a bt ct 3.

(1)

Угловая скорость вращения колеса есть первая производная от углового пути по времени:

	(t)	d (t)	b 3ct 2 .	(2)
		dt

18

Угловое ускорение колеса есть первая производная от угловой скорости по времени:

	t	d t	6ct .	(3)
		dt

Связь между линейной скоростью точек, лежащих на ободе колеса, и угловой скоростью колеса определяется формулой

ωR R(b 3ct2 ).

(4)

Тангенциальное ускорение точек, лежащих на ободе колеса:

	a	d	R	d		R 6Rct .	(5)
		dt		dt

Нормальное ускорение точек, лежащих на ободе колеса:

	2	R 2 (b 3ct 2 )2
an			R(b 3ct 2 )2 .	(6)
	R	R

Мы нашли все искомые величины как функции времени. Чтобы ответить на вопрос задачи, надо в уравнения (2) – (6) подставить t 3 c:

t

t 3 c

b 3c 32 (3 3 2 9)

рад

57

рад

;

c

c

t

t 3 c

6c 3 6 2 3

рад

36

рад

;

c

c

2

t

t

3 c

R b 3c 32 0,1 57 5,7

м

;

c

м

a

t

t 3 c

6Rct 6 0,1 2 3 3,6

;

c

an t

t

3 c

R b 3ct 2 2 0,1 57 2 324,9

м

.

рад

м

c

Ответ: 57

рад

; 36

; 5, 7

; a

3,6

м

; a

324,9

м

.

с

с

22

с

c2

n

c2

Пример 1.4. Частица движется вдоль оси

x

по закону x(t) t2 bt3 ,

где и b – положительные постоянные. В момент t 0 сила, действующая на частицу, равна F0 . Найти значение силы Fx в точке поворота и в момент, когда частица опять окажется в точке x 0 .

19

Дано:

x(t) t2 bt3

, b const

при t 0 , Fx F0

Fx x 0 ?

Fx x 0 ?

Решение. Запишем уравнение движения (2-й закон Ньютона) для частицы, движущейся вдоль оси x :

			max Fx .			(1)
Проекция скорости на ось x					частицы есть
первая производная от координаты					x	по времени,
найдем ее, используя условие задачи
			dx t	2 t 3bt2	.	(2)
	x
			dt

Проекция ускорения на ось x частицы есть первая

	производная от проекции						скорости на ось		x по
	времени:
	a			d	x		d 2 x	2 6bt .	(3)
		x		dt			dt2
	Подставим ax из (3) в уравнение (1):
	m 2 6bt Fx .								(4)

В уравнении (4) неизвестна масса частицы m , найдем ее из начальных условий. Известно, что в начальный момент при t 0 Fx F0 , подставим

это условие в (4), получим

m2 F0 ,

откуда

								m					F0
													2 .						(5)
Подставив (5) в (4), получим
						F		F0		2 6bt .									(6)
						x		2
В точке поворота частицы ее скорость x 0 . Положим в (2) x 0 , получим
0 2 t	3bt2 , где		t – время, когда частица окажется в точке поворота. По-
1	1		1
скольку t1 0 , то
								t				2		.					(7)
							1					3b
Подставим (7) в (6) и найдем значение силы Fx в точке поворота:
	F			F0	2 6bt				F0				2 6b			2		F0	2 F .
	1x			2		1												2	0
									2							3b

Теперь найдем время t2 , когда частица опять окажется в точке					x 0 .
Для этого в законе движения x(t) t2 bt3		приравняем x t		0, получим
			2
0 t2	bt3 , или t		.		(8)
2	2	2	b

20