физика

2. ЭЛЕКТРОМАГНЕТИЗМ

(Основные формулы)

2.1. Электростатическое поле в вакууме

Закон Кулона в скалярном виде:

qq F k r2 ,

где F – модуль силы взаимодействия между точечными зарядами q и q ;

k		1		9 109 м / Ф ;		8,85 10 12	Ф / м – электрическая постоянная; q	–
					0
	4
			0

точечный заряд, создающий электростатическое поле; q – точечный заряд,

внесенный в электростатическое поле; r – расстояние между зарядами q и q . Напряженность электростатического поля

	E(r )	F(r )	,
		q

где F(r ) – сила, действующая на точечный заряд q , внесенный в данную

точку поля с радиусом-вектором r . Потенциал электростатического поля

	(r )	U (r )	,
		q

где U( r ) – потенциальная энергия точечного заряда q , помещенного в дан-

ную точку поля.

Напряженность и потенциал поля точечного заряда q :

E(r )		kq			r ;
		r3
(r )		k	q			.
			r
Принцип суперпозиции полей:
	n
E(r )		Ei (r ) ;
i	1
	n
(r )			i (r ) ,
i	1

где Ei (r ) – напряженность поля i-го заряда системы в рассматриваемой точке, создаваемого им в отдельности; E(r ) – напряженность поля, создаваемо-

го системой зарядов в рассматриваемой точке.

Связь напряженности и потенциала электростатического поля:

41

E(r ) (r ) gradφ .

где

i

j

k .

x

y

z

Работа, совершаемая силами электрического поля при перемещении

точечного заряда q из точки 1 в точку 2, определяется формулой

2

A12

q (E, dl ) .

1

Работа сил электростатического поля через разность потенциалов 1 и

2 :

A12

q( (r1)

(r2 )) q( 1

2 ) ,

где

(r1)

1

– потенциал поля в точке с радиусом-вектором r1 ; (r2 )

2 –

потенциал поля в точке с радиусом-вектором r2 .

Теорема о циркуляции вектора

E :

	(E, dl )			0 .
	(L)
Теорема Гаусса:
		1		n
	(E, dS )			qi ,
		0 i
(S )				1

n

qi – суммарный заряд, охватываемый поверхностью (S ) .

i 1

Линейная плотность заряда (в случае равномерного распределения заряда)

dq q , dl l

где l – длина нити, несущая заряд q.

Поверхностная плотность заряда (в случае равномерного распределения заряда)

dq q , dS S

где S – площадь поверхности, несущая заряд q.

Объемная плотность заряда (в случае равномерного распределения заря-

да)

dq q , dV V

где V – объем тела, несущий заряд q.

42

2.2. Постоянный ток

Сила тока

I dqdt ,

где dq – заряд, перенесенный через поперечное сечение проводника за время dt . Для постоянного тока

I qt .

Плотность тока

j SI ,

где S – площадь поперечного сечения проводника. Закон Ома для однородного участка цепи:

I UR ,

где I – сила тока; U – разность потенциалов (напряжение) на концах участка; R – электрическое сопротивление проводника.

Закон Ома для неоднородного участка цепи:

U

I R r ,

где – электродвижущая сила (ЭДС), действующая на рассматриваемом участке цепи; r – внутреннее сопротивление источника тока.

Закон Ома для замкнутой цепи:

I R r .

Электрическое сопротивление однородного линейного проводника

R Sl ,

где – удельное электрическое сопротивление; l – длина проводника; S – площадь поперечного сечения проводника.

Первое правило Кирхгофа:

n
Ik	0 .
k 1
Второе правило Кирхгофа:
k	n
Ii Ri	k .
i 1	k 1

Закон Джоуля – Ленца для постоянного тока:

43

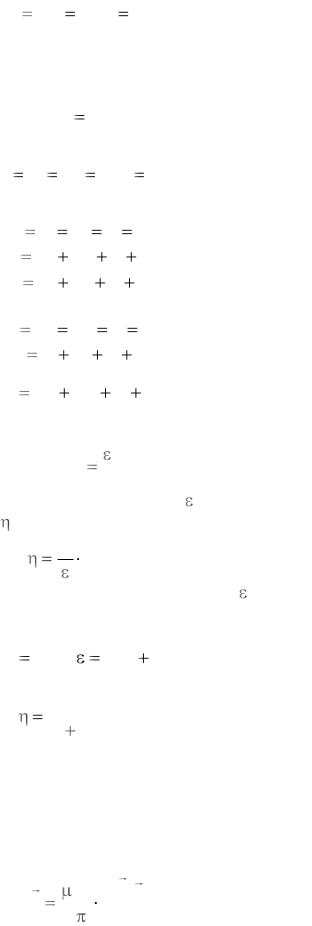
Q

UIt

RI 2t

U 2

t ,

R

где Q – количество выделившейся теплоты при прохождении тока I по про-

воднику за время t .

Работа тока

A

UIt .

Мощность тока

A

I 2 R

U 2

P

UI

.

t

R

Для последовательного соединения N проводников:

I

I1

I2 ...

I N ;

U

U1

U2 ...

U N ;

R

R1

R2 ...

R N .

Для параллельного соединения N проводников:

U

U1

U2 ...

U N ;

I

I1

I2 ...

I N ;

1

1

1

...

1

.

R

R1

R2

RN

Сила тока короткого замыкания

Iк.з

,

r

где r – внутреннее сопротивление источника тока; – ЭДС источника тока. КПД источника тока :

U (100 %),

где U – напряжение на концах внешнего участка цепи; – ЭДС источника тока.

Поскольку согласно закону Ома для однородного участка и полной цепи

U IR и			I( R r ) ,
то
	R		100 % ,
	R	r

где R – сопротивление внешней части цепи; r – внутреннее сопротивление источника тока.

2.3. Магнитное поле в вакууме

Закон Био – Савара – Лапласа:

dB	0 I	[dl , r ]		,
	4		r3

44

где dB – индукция магнитного поля элемента тока dI мой точке; r – вектор, проведенный от dI к этой точке; магнитная постоянная.

Модуль вектора dB определяется выражением

Idl в рассматривае-

0	4 10 7	Гн / м –

dB		dB			0I		sin dl	,
				4			r2

где – угол между вектором r и направлением тока в элементе провода.

Если все dB от различных элементов тока сонаправлены, то

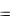B dB .

Закон Ампера:

		dFA I[dl , B] ,
где	dFA	– сила, действующая на элемент провода dl									с током I в магнитном
поле с индукцией B .
	Модуль силы Ампера
		dFA		dFA				IBsin	dl ,
где	– угол между направлением dl							и B .
	Если все dFA , действующие на различные элементы тока сонаправле-
ны, то
		FA						dFA ,
где dFA – модуль силы Ампера.
	Магнитный момент тонкого плоского контура с током
				Pm				nIS ,
где
	n – единичный вектор нормали к плоскости контура, образующий пра-
вый винт с направлением тока; I – сила тока, протекающего по контуру; S –
площадь поверхности, ограниченной контуром.
	Сила Лоренца
		F		qE				q[ , B],
где qE		Fэ – электрическая составляющая силы Лоренца; q[ , B] Fм – маг-
нитная составляющая силы Лоренца.
	Модуль магнитной составляющей силы Лоренца
		Fм			q			Bsin	,
где – угол между направлением скорости частицы											и направлением маг-
нитного поля B .
	Закон полного тока (теорема о циркуляции вектора B ):
									N
		(B, dl )						B dl	0	Ik ;
		(L)		(L)					k	1

45

	N
	где	I k – алгебраическая сумма токов, охватываемых контуром (L).
	k	1
		Ток, текущий через поверхность (S) , можно представить через плот-
	ность тока j:
		I	( j, dS )		| j || n | cos				dS	jndS ,
		(S )		(S )					(S )
		Поток вектора B	через поверхность (S):
			(B, dS )		| B || n |cos				dS	BndS ,
			(S )	(S )					(S )
	где	– угол между единичным вектором нормали
										n к поверхности (S) и
	вектором магнитной индукции B			в данной точке поверхности.
		Работа сил магнитного поля по перемещению замкнутого контура с то-
	ком в магнитном поле
			A12	I Ф I (Ф2					Ф1) ,
	где Ф1 и Ф2 – значения магнитного потока вектора									B через ограниченную
	контуром поверхность в начальном и конечном положениях.
		Потокосцепление (полный поток) через N одинаковых витков (солено-
	ид)	N ;
	где Ф – магнитный поток через один виток.
		Закон Фарадея:
						d		,
				i
						dt
	где i	– электродвижущая сила индукции, возникающая в контуре при изме-
	нении потокосцепления.

2.4 Электромагнитные колебания

	Дифференциальное уравнение гармонических электрических колеба-
ний в идеальном колебательном контуре:
			q	02q 0,
где q		dI	– изменение тока в контуре в единицу времени; q		– заряд на об-
		dt

кладках конденсатора.

Собственная циклическая частота колебаний контура

1

0 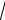LC ,

где L – индуктивность катушки; C – емкость конденсатора.

46

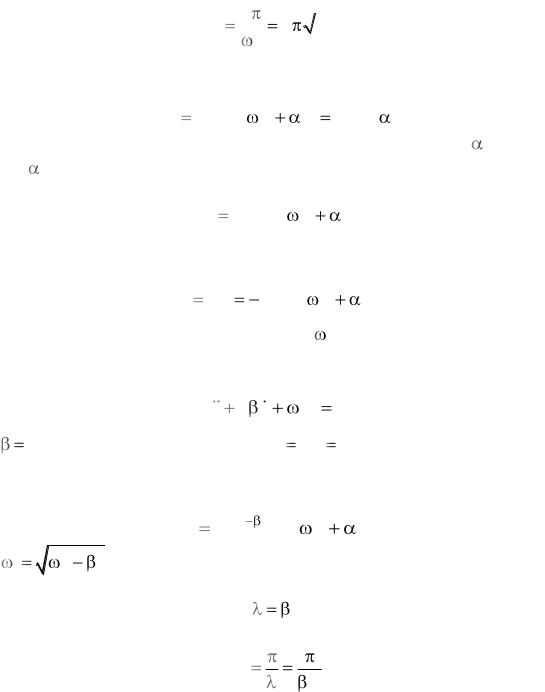
Формула Томсона:

			2
		T				2		LC ,
					0
где Т – период гармонических колебаний.
Закон изменения заряда q			на обкладках конденсатора:
q qmcos(					0t		0 )		qmcos ,
где q – заряд в момент времени t;					qm – амплитудный заряд;						– фаза коле-
баний; 0 – начальная фаза колебаний.
Закон изменения напряжения на конденсаторе
	U		Umcos(				0t		0 ) ,
где U m – амплитуда напряжения.
Закон изменения силы тока в катушке индуктивности:
I		dq			Imsin(			0t	0 ) ,
		dt

где I – сила тока в момент времени t; Im 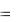0qm – амплитуда силы тока.

Дифференциальное уравнение затухающих электрических колебаний в контуре:

			q 2 q	02q 0 ,
	где	R	– коэффициент затухания; q	dq	I	– ток.
		2L		dt

Закон изменения заряда на обкладках конденсатора при затухающих колебаниях:

		q q e tcos( 't	0	) ,
		m
где '	2 2 – частота затухающих колебаний контура.

0

Логарифмический декремент затухания

T .

Добротность контура

Q T .

47

2.5. Примеры решения задач

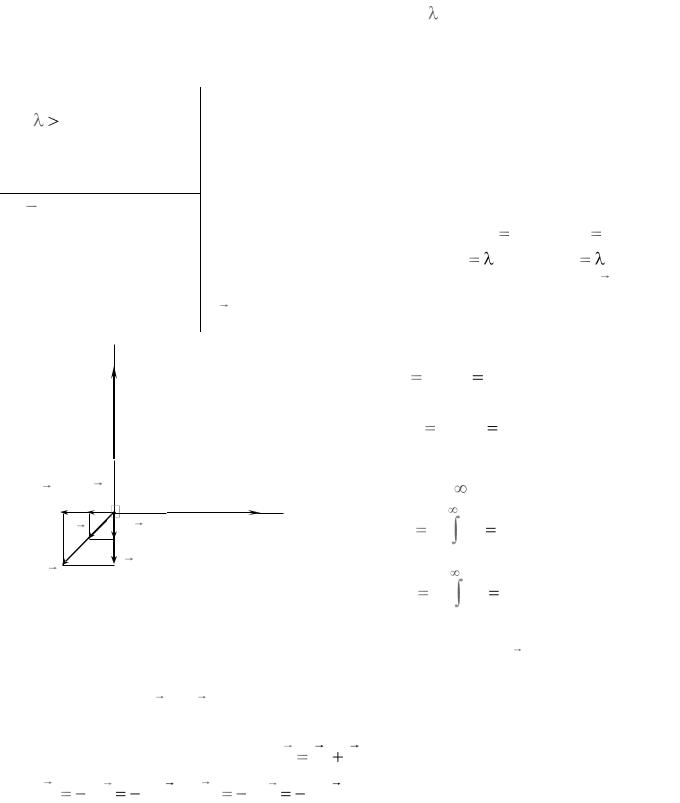
Пример 2.1. По двум тонким длинным нитям равномерно распределен одинаковый заряд с линейной плотностью заряда . Найти модуль напряженности электрического поля E в точке O , расположенной на пересечении нитей, на расстоянии a от ближайших концов нитей.

Дано:

0 , a

E ?

								y
		dy						dq2
	2	y
								a
	E1 dE1
							O
	dE							dE2 a
						1
	E							E2
								Рис. 2.1

Решение. Поместим точку O в начало координат

осей Ox и Oy (рис. 2.1). Обозначим стержень, расположенный вдоль оси x, цифрой 1, а стержень вдоль оси y – цифрой 2. Ближайшие концы стержней расположены от точки O на расстоянии a , противоположные концы уходят в бесконечность. На стерж-

нях выделим элементы длиной dl1	dx	и dl2	dy ,
несущие точечные заряды dq1	dx и	dq2	dy .

Эти заряды создадут в точке O напряженности dE1 и

dE2 , модули которых равны

dE1

k

dq1

k

λdx

,

(1)

x2

x2

dE2

k

dq2

k

λdy

.

(2)

y2

y

2

Проинтегрируем выражения (1) и (2) в

dq1

x

пределах от a до

, получим

x

dx

E1

kλ

dx

kλ

,

(3)

a x2

a

E

kλ

dy

kλ

.

(4)

2

a y2

a

По принципу суперпозиции полей напряженность поля E , создаваемого нитями в точке O , может быть найдена как геометрическая сумма напря-

женностей полей E1 и E2 , создаваемых каждым заряженным телом (в нашем случае нитями) в отдельности, т. е.

				E	E1 E2 ,		(5)
где E	E i	kλ	i и E	E j	kλ	j .
1	1	a	2	2	a

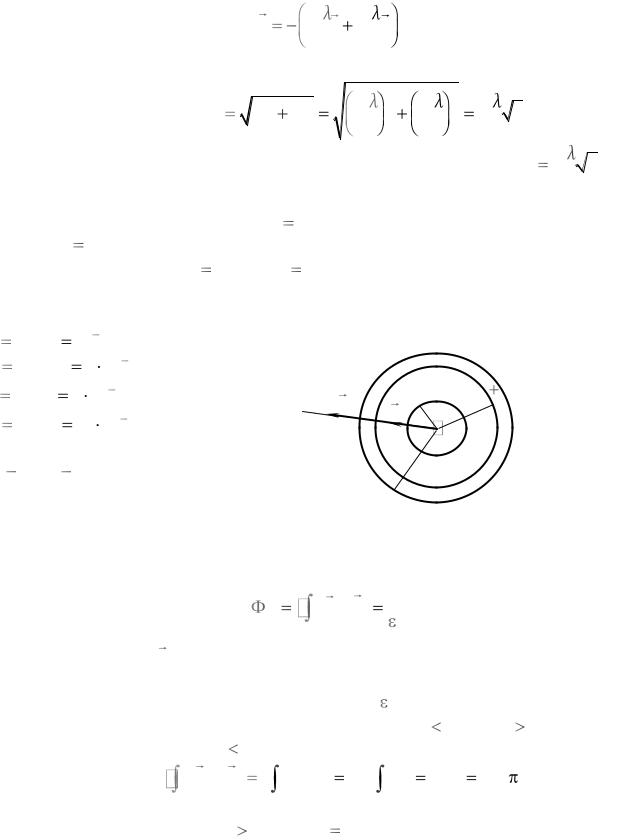
Тогда

48

E

k

i

k

j .

(6)

a

a

Модуль напряженности поля E равен

k

2

k

2

k

E2

E2

E

2 .

(7)

1

2

a

a

a

k

Ответ: E

2 .

a

Пример 2.2. Шар радиусом R

10 см равномерно заряжен по объему

зарядом Q

5 нКл . Найти напряженности поля в точках, отстоящих от цен-

тра шара на расстояниях r1 5 см и r2

15 см .

Дано:

Решение.

R

10 см

10 1 м

S2

Q

5 нКл

5 10 9 Кл

r1

Q

r1

5 см

5 10

2

м

R

E1

n

r

15 см

15 10 2 м

2

q1 S

E

? E

?

r2

1

1

2

Рис. 2.2

Будем решать задачу по теореме Гаусса:

(E, dS )

q

.

(1)

E

S

0

Поток вектора E напряженности электростатического поля через про-

извольную замкнутую поверхность S равен алгебраической сумме зарядов,

охватываемых этой поверхностью и деленной на

0 .

В нашей задаче надо рассмотреть два случая: 1) r

R и 2) r

R .

1. Рассмотрим случай r

R .

(E , dS )

E

dS

E

dS E S

E 4

r 2 .

(2)

1

1n

1

1 1

1

1

S1

(S1)

(S1)

Здесь учтено, что поскольку Q

0 , то E1n

E1 и в каждой точке сферы

S1

модуль напряженности одинаков.

Так как шар заряжен равномерно, то его объемная плотность в каждой точке одинакова и равна

49

											Q					q1					или q															Q		V				,
										V					V													1							V				1
															1
где q			– заряд шара, ограниченный сферой радиусом r																																								; V			– объем сферы ра-
	1																																									1	1
диусом r .
			1
										Q										Q								4					r3							Qr3
								q				V																															1	.												(3)
								1	V				1					4				R			3			3						1							R3
															3
Подставим (2) и (3) в (1):
																				Qr3
									E 4					r						1								,
									1						1						0 R3
														E1										Qr1									.																							(4)
																				4						0 R3
		2. Рассмотрим случай r							R .
		Как и в первом случае E2n											E2 :
								(E , dS )							E										dS									E S					2				E 4 r2 .													(5)
									2						2																				2								2						2
								(S2 )												( S2 )
		Так как внутрь сферы							S2				входит весь заряд шара Q ,																																							то в соответ-
ствии с теоремой Гаусса (1)
										E 4					r2								Q				,
												2			2
																									0
откуда
															E2													Q							.																					(6)
																				4											r2
																												0 2
		Произведем вычисления:
E1			Qr1					5 10 9 5 10 2														В										25 10										11					В					2,27 10	3		В			;
	4			0R3		4 3,14 8,85 10 12 (10									1)3							м						11 10 11														10 3					м								м
				Q				5 10 9																							В 5 10 9																			В		3		В		.
	E2																																																			2 10
				4 0r22		4		3,14 8,85 10 12					(15 10 2 )2																		м						2,5 10 12 м																	м
																																											3			В							3				В
															Ответ: E1																				2,27 10														; E2 2 10											.
																																														м											м
		Пример 2.3. Тонкое полукольцо радиусом R																																									5 см заряжено равно-
мерно зарядом q								20 нКл . Найти модуль напряженности электрического по-
ля E и потенциал								в центре кривизны этого полукольца.

50