Sluchaynye_protsessy

ные

ξ(t)

ξ(ω1,t)

t = t1

2.ВВЕДЕНИЕ В ТЕОРИЮ СЛУЧАЙНЫХ ПРОЦЕССОВ

2.1.Определение случайного процесса. Классификация случайных процессов

В теории случайных процессов изучаются задачи построения и анализа математиче- ских моделей случайных явлений, развивающихся во времени. Как математический объект случайный процесс определяется следующим образом. Считается, что задано некоторое ве-

роятностное пространство {Ω, F, P}, т.е. считается, что имеется множество элементарных исходов Ω, σ -алгебра F подмножеств множества Ω и вероятность P = P(A) для каждого множества (события) A F (A Ω) .

Случайным процессом называется функция ξ(ω,t) , ω Ω, t T , которая для любого

фиксированного t T является измеримой функцией аргумента ω .

Аргумент t здесь понимается как время из некоторого промежутка времени T , а аргу- мент ω – это элементарный исход (случай). При фиксированном мы получаем функ- цию случая ξ(ω,t1) , т. е. случайную величину, которая называется сечением процесса в мо- мент времени t1. Если зафиксировать случай ω = ω1, то получим функцию времени , которая называется реализацией, траекторией или выборочной функцией случай-

ного процесса.

На рис. 1 приведены три реализации (траектории) случайного процесса и его сечение в момент времени t1. В качестве реализаций взяты графики температуры воздуха по метео-

станции Минск в феврале 1998, 1999, 2000 годов.

В связи с тем, что чаще всего множество Ω оказывается недоступным, т. е. элементар- исходы не наблюдаются, случайный процесс обозначают как функцию только времени , а зависимость от ω подразумевается.

Назовем любое множество G дискретным, если оно конечное или счетное, и непрерыв- ным, если оно несчетное.

Случайные процессы классифицируются по виду множеств T и G , где G – множество возможных значений случайного процесса. Эти множества могут быть непрерывными или дискретными, в связи с этим различают 4 класса случайных процессов.

1. T и G – непрерывные множества. Это процесс с непрерывным временем и непре- рывным множеством значений или процесс общего типа. Пример реализаций такого процес- са представлен на рис. 2.1.

2. T дискретно, G непрерывно. Это процесс с дискретным временем и непрерывным множеством значений или случайная последовательность. Пример реализации такого про- цесса представлен на рис. 2.2.

3. T непрерывно, G дискретно. Это процесс с непрерывным временем и дискретным множеством значений или дискретный случайный процесс. Пример реализации такого про- цесса представлен на рис. 2.3.

4. T дискретно, G дискретно. Это процесс с дискретным временем и дискретным мно- жеством значений или дискретная случайная последовательность. Пример реализации такого процесса представлен на рис. 2.4. Случайные последовательности часто называют времен- ными рядами.

11

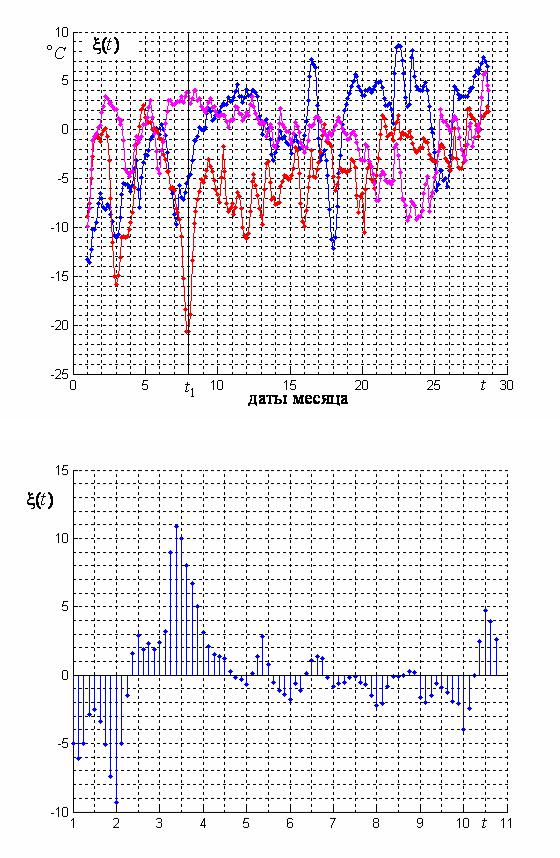
Рис. 2.1. Три реализации случайного процесса общего типа

Рис. 2.2. Реализация случайной последовательности

12

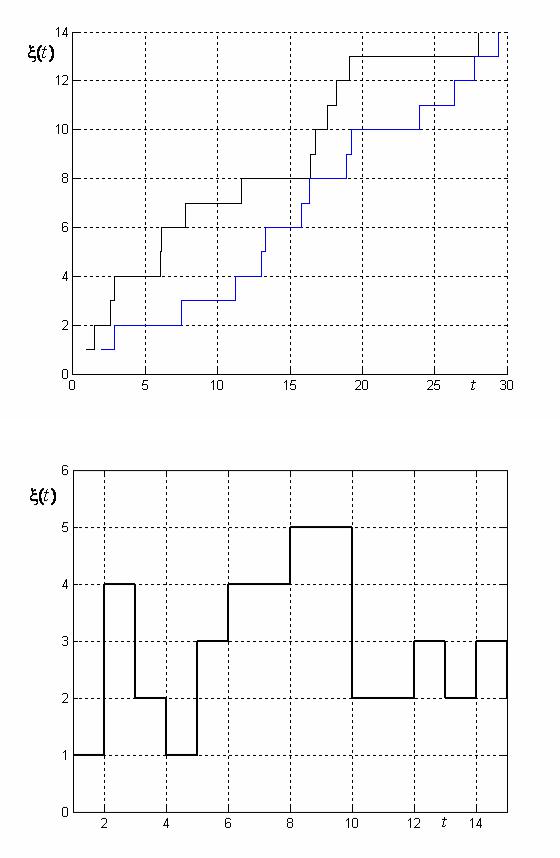
Рис. 2.3. Две реализация дискретного случайного процесса

Рис. 2.4. Реализация дискретной случайной последовательности

13

2.2. Конечномерные распределения случайного процесса

Рассмотрим случайный процесс ξ(t) и зафиксируем n моментов времени t1,...,tn . Мы

получим n сечений процесса ξ1 = ξ(t1) , ξ2 = ξ(t2 ) ,…, ξn = ξ(tn ) .

Конечномерной ( n -мерной) функцией распределения случайного процесса ξ(t) называ- ется функция распределения случайного вектора ξ = (ξ1,...,ξn ) , компоненты которого ξi являются сечениями процесса в моменты t1,...,tn :

Fξ (x1,...,xn ,t1,...,tn ) = P(ξ(t1) < x1,...,ξ(tn ) < xn ) .	(2.1)
Конечномерная функция распределения случайного процесса ξ(t) является функцией	2n
аргументов: n аргументов x1 ,...,xn и n аргументов t1,...,tn . Она должна обладать свойст-
вами симметрии и согласованности.

Свойство симметрии заключается в том, что любые два аргумента функции распределе- ния xi и x j можно менять местами, поменяв при этом местами соответствующие аргументы

ti и t j :

Fξ (x1,..., xi ,..., x j ,..., xn ,t1,...,ti ,...,t j ,...,tn ) = = Fξ (x1,..., x j ,...,xi ,..., xn ,t1,...,t j ,...,ti ,...,tn ) .

Для двухмерной функции распределения это свойство выражается равенством

Fξ (x1, x2,t1,t2 ) = Fξ (x2 , x1, t2 ,t1) .

Свойство согласованности выражается условием

) =

lim F

(x ,..., x

k −1

, x

k

, x

k +1

,..., x

n

,t ,...,t

k −1

,t

k

,t

k +1

,...,t

n

xk →∞

ξ

1

1

=

lim

F

(x ,..., x

k −1

, x

k +1

,..., x

n

,t ,...,t

k −1

,t

k

+1

,...,t

n

) ,

xk →∞

ξ

1

1

т. е. если в n -мерной функции распределения аргумент xk

заменить на ∞ , то мы получим

(n −1) -мерную функцию распределения

(этот

аргумент

исчезает

из

списка аргументов

функции распределения вместе с соответствующим ему аргументом tk ).

Конечномерной ( n -мерной) плотностью вероятностей случайного процесса ξ(t) называ- ется смешанная производная n -го порядка от n -мерной функции распределения:

		,...,tn ) =		∂n
fξ (x1	,...,xn ,t1				Fξ (x1,..., xn ,t1,...,tn ) .	(2.2)
			∂x1
				,...,∂xn

Конечномерную функцию распределения (2.1) или конечномерную плотность вероятно- сти (2.2) называют конечномерным распределением случайного процесса.

Совокупность конечномерных распределений для любого конечного n и произвольных моментов времени t1,...,tn называется семейством конечномерных распределений случайно-

го процесса.

Случайный процесс наиболее полно описывается семейством конечномерных распреде- лений. Так как это семейство бесконечное, то такое описание представляется чрезвычайно сложным. Выход состоит в том, что рассматривают определенные классы случайных про- цессов. Например, можно рассматривать класс процессов, которые описываются семейством

одномерных распределений fξ (x,t) , или, если все одномерные распределения совпадает, то одним одномерным распределением. Такой процесс, естественно, будет обладать тривиаль-

14

(2.3)

– символ ма-

ными свойствами а не слишком широкой областью применения. Второй класс процессов – процессы, описываемые семейством двухмерных распределений fξ (x1, x2 ,t1,t2 ) для любых

t1, t2 из интересующего нас промежутка времени T . Этот класс процессов имеет более ши- рокий спектр свойств и более широкое применение.

2.3. Математическое ожидание и дисперсия случайного процесса

Будем рассматривать случайные процессы, для которых существуют конечномерные плотности вероятности. К таким процессам относятся процессы с непрерывным множеством значений. Для процессов с дискретным множеством значений более удобным по сравнению с функциями распространения будет описание с помощью вероятностей возможных значе- ний.

Математическим ожиданием E(x(t)) случайного процесса x(t) называется функция aξ (t) , определяемая выражением

∞

aξ (t) = E(ξ(t)) = ò xfξ (x,t)dx ,

−∞

где fξ (x,t) – одномерная плотность вероятности случайного процесса, E(×) тематического ожидания (усреднения). Математическое ожидание aξ (t) является функцией

времени и представляет собой функцию, возле которой группируются все реализации слу- чайного процесса. Математическое ожидание характеризует среднюю тенденцию развития процесса во времени. На рис. 2.5 представлены реализации и математическое ожидание слу-

чайного процесса вида

x(t) = a + bt ,

(2.4)

где α и b – независимые случайные величины, распределенные по нормальным законам N(aα ,σα2 ) , N (aβ ,σβ2 ) соответственно. Выражение математического ожидания имеет вид

aξ (t) = aα + aβt .

Реализации этого процесса имеют тенденцию к возрастанию, в связи с чем возрастающей является и функция математического ожидания.

Дисперсией D(x(t)) случайного процесса x(t) называется математическое ожидание квадрата отклонения процесса от его математического ожидания:

σξ2 (t) = D(ξ(t)) = E((ξ(t) − aξ (t))2 ) =	∞
	ò(x − aξ (t))2 fξ (x,t)dx ,	(2.5)

−∞

где fξ (x,t) – одномерная плотность вероятности случайного процесса, D(×) – символ дис-

персии. Дисперсия процесса является функцией времени σξ2 (t) , которая характеризует

среднее отклонение реализаций процесса от его математического ожидания в любой момент времени t . На рис. 2.5 изображена функция σξ (t) = σξ2 (t) – среднее квадратичное откло- нение (с.к.о.) случайного процесса (2.4). Дисперсия процесса (2.4) определяется выражением

σξ2	o o	o	o o	o
	(t) = E((α+ βt)2 ) = E((α)2 ) + E(αβt) + E((βt)2 ) = σα2 + σβ2t2 .

15

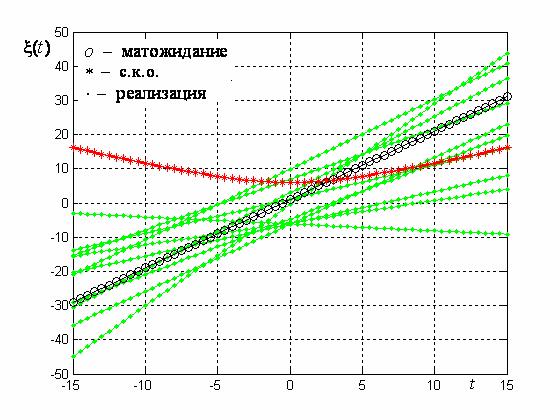
Для данного процесса реализации имеют тенденцию с течением времени все более откло- няться от функции математического ожидания, поэтому с.к.о. процесса является возрастаю- щей функцией.

Рис. 2.5. Реализации, математическое ожидание и среднее квадратичное отклонение случайного процесса (2.4).

2.4. Ковариационная функция случайного процесса

o

Пусть ξ(t) – случайный процесс, и ξ(t) = ξ(t) − E(ξ(t)) – центрированный случайный процесс.

Ковариационной функцией Rξ (t1,t2 ) случайного процесса ξ(t) называется коэффициент ковариации между сечениями процесса в два момента времени t1, t2 :

o	o
Rξ (t1,t2 ) = cov(ξ(t1),ξ(t2 )) = E(ξ(t1) ξ(t2 )).		(2.6)

Для процессов, имеющих конечномерные плотности вероятностей, ковариационная

функция рассчитывается по формуле

Rξ (t1,t2 ) =	∞	∞	− aξ (t1))(x2	− aξ (t2 )) fξ (x1, x2 ,t1,t2 )dx1dx2 ,
	ò	ò(x1			(2.7)

−∞ −∞

где fξ (x1, x2 ,t1,t2 ) – двухмерная плотность вероятности случайного процесса.

Ковариационная функция является функцией двух аргументов t1, t2 . Она характеризует силу линейной стохастической связи между двумя сечениями случайного процесса в момен- ты времени t1, t2 .

16

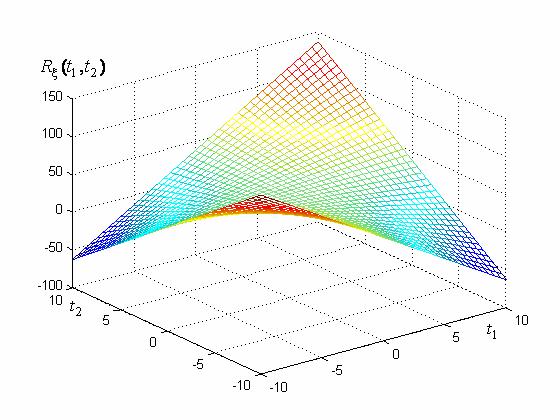
На рис. 2.6 представлена ковариационная функция случайного процесса (2.4). Она опре-

деляется выражением

		o o	o o		o	o	) = σ2	+ σ2t t
R (t ,t
	2	) = E((α+ βt )(α+ βt		2	)) = E((α)2 ) + E(β2 t t				.
ξ 1		1				1 2	α	β 1 2

	Рис. 2.6. Ковариационная функция случайного процесса (2.4)
Ковариационная функция имеет следующие свойства.
1.	Это симметричная функция своих аргументов:
		Rξ (t1,t2 ) = Rξ (t2,t1).
Действительно, имеем
	o	o	o	o
	Rξ (t1,t2 ) = E(ξ(t1) ξ(t2 )) = E(ξ(t2 ) ξ(t1)) = Rξ (t2 ,t1) .
2.	Дисперсия процесса в момент времени t		определяется как значение ковариационной
функции в точке t,t :

Dξ (t) = σ2ξ (t) = Rξ (t,t) .

Действительно,

o o	o	2	(t)) = D(ξ(t)) = σ2
R (t,t) = E(ξ(t) ξ(t)) = E(ξ				(t) .
ξ			ξ

3. Ковариационная функция подчиняется неравенству

Rξ2 (t1,t2 ) ≤ Rξ (t1,t1)Rξ (t2 ,t2 ) .

17

Взаимной ковариационной функцией процессов

называется коэффициент

Это свойство является интерпретацией известного неравенства Шварца: для любых случай-

o

ных величин справедливо неравенство E2 (uv) ≤ E(u2 )E(v2 ) . Если выбрать u = ξ(t1) ,

o

v = ξ(t2 ) , то получим неравенство для ковариационной функции.

Корреляционной функцией случайного процесса называется коэффициент корреляции между сечениями процесса в моменты t1, t2 , или, иначе, нормированная ковариационная функция:

	rξ (t1,t2 ) =		Rξ (t1,t2 )			.	(2.8)
			Rξ (t1,t1)Rξ (t2	,t2 )

Свойства корреляционной функции автоматически вытекают из соответствующих свойств ковариационной функции:

1.rξ (t1,t2 ) = rξ (t2,t1) ;

2.rξ (t,t) = 1;

3.rξ2 (t1,t2 ) ≤ 1.

2.5.Взаимная ковариационная функция двух случайных процессов

Двумерной совместной функцией распределения процессов ξ1(t) и ξ2 (t) называется

функция Fξ (x, y,t1,t2 ) , определяемая выражением
Fξ (x, y,t1,t2 ) = P(ξ1(t1) < x, ξ2 (t2 ) < y) ,	(2.9)

где t1, t2 – два момента времени.

Двумерной совместной плотностью вероятности процессов ξ1(t) и ξ2 (t) называется смешанная производная второго порядка от совместной функции распределения:

fξ (x, y,t1,t2 ) = ∂2 Fξ (x, y,t1,t2 ) .

∂x∂y

ξ1(t) , ξ2 (t)

ковариации между сечениями ξ1(t1) , ξ2 (t2 ) этих процессов:

Rξ1 ,ξ2 (t1,t2 ) = cov(ξ1(t1),ξ2 (t2 )) = E(ξ°1(t1)ξ°2 (t2 )) =

∞ ∞

= ò ò(x1 − aξ1 (t1))(y2 − aξ2 (t2 )) fξ (x, y,t1,t2 )dxdy .

−∞ −∞

(2.10)

(2.11)

Взаимная ковариационная функция характеризует силу линейной связи между сечениями двух процессов в два различных момента времени t1, t2 . Она обладает следующим очевид-

ным свойством:

Rξ1 ,ξ2 (t1,t2 ) = Rξ2 ,ξ1 (t2 ,t1) .

18

ξ(t)

2.6. Стационарный случайный процесс

Случайный процесс ξ(t) называется стационарным в строгом или узком смысле, если его

конечномерные распределения инвариантны к сдвигу по оси времени, т. е. не зависят от это- го сдвига.

Для конечномерных распределений свойство инвариантности записывается в виде
Fξ (x1,..., xn ,t1,...,tn ) = Fξ (x1,..., xn ,t1 + s,...,tn + s) ,	(2.12)

где s – некоторое число, характеризующее сдвиг по оси времени.

Функция распределения, стоящая слева в равенстве (2.12), определяет свойства процесса в моменты времени t1,...,tn . Функция распределения, стоящая справа, определяет свойства

процесса в сдвинутые по оси времени на величину s моменты времени t1 + s,...,tn + s . Ра- венство этих функций распределения означает, что свойства процесса в моменты t1,...,tn такие же, как и в моменты t1 + s,...,tn + s . Определение (2.12) означает, что свойства про-

цесса не изменяются с течением времени. Таких процессов в природе не существует, но если рассматривать процесс на некотором конечном промежутке времени, то предположение ста- ционарности может оказаться допустимым.

Теорема. Если процесс стационарен в узком смысле, то его математическое ожида- ние и дисперсия не зависят от времени, а ковариационная функция Rξ (t1,t2 ) не зависит от t1 и t2 в отдельности, а зависит лишь от их разности τ = t1 − t2 , т. е. является функцией не двух аргументов t1, t2 , а одного аргумента τ = t1 − t2 :

Rξ (t1,t2 ) = Rξ (t1 − t2 ) = Rξ (τ) .

Действительно, условие стационарности (2.12) для одномерной плотности вероятности имеет вид fξ (x1,t1) = fξ (x1,t1 + s) . Так как это равенство выполняется для любого s ,

то, выбрав s = t1, получим

fξ (x1,t1) = fξ (x1,t1 − t1) = fξ (x1,0) = fξ (x1) .

Мы видим, что одномерная плотность вероятности стационарного в узком смысле процесса не зависит от времени. Тогда для математического ожидания и дисперсии получим

aξ (t) = E(ξ(t)) =			∞	=	∞		= aξ = const ,
			ò x1 fξ (x1,t1)dx1		ò x1 fξ (x1)dx1
			−∞		−∞
o	∞				∞	− aξ )2 fξ (x1)dx1 =σξ2 = const.
σξ2 (t) = E(ξ2 (t)) =	ò (x1	− aξ )2 fξ (x1,t1)dx1 = ò (x1
	−∞				−∞

Запишем теперь условие инвариантности (2.12) для двухмерной плотности вероятности:

fξ (x1, x2 ,t1,t2 ) = fξ (x1, x2,t1 + s,t2 + s) .

Выбрав здесь s = −t1 , получим

fξ (x1, x2 ,t1,t2 ) = fξ (x1, x2 ,t1 − t1,t2 − t1) = fξ (x1, x2 ,τ).

Мы видим, что двухмерная плотность вероятности стационарного в узком смысле процесса не зависит от каждого из двух аргументов t1, t2 отдельно, а зависит лишь от их разности

τ = t2 − t1 . Запишем выражение для ковариационной функции такого процесса

19

∞ ∞

Rξ (t1,t2 ) = ò ò(x1 − aξ (t1))(x2 − aξ (t2 )) fξ (x1, x2 ,t1,t2 )dx1dx2 =

−∞ −∞

∞∞

=ò ò(x1 − aξ )(x2 − aξ ) fξ (x1, x2 ,t1 − t2 )dx1dx2 = Rξ (t2 − t1) = Rξ (τ) .

−∞ −∞

Теорема доказана.

Случайный процесс ξ(t) называется стационарным в широком смысле, если его матема-

тическое ожидание и дисперсия не зависят от времени, а ковариационная функция зависит от разности своих аргументов.

Из доказанной выше теоремы следует, что из стационарности в узком смысле следует стационарность в широком смысле. Обратное утверждение в общем случае неверно. Обрат- ное утверждение верно лишь в случае, когда процесс ξ(t) является нормальным (гауссов-

ским). Гауссовский случайный процесс определен в разделе 2.7.

Свойства ковариационной функции стационарного случайного процесса приобретают другую форму. Перечислим их.

1.Rξ (τ) = Rξ (−τ) .

2.Dξ = σξ2 = Rξ (0).

3.Rξ2 (τ) ≤ Rξ2 (0) , или Rξ (τ) ≤ Rξ (0) .

Эти свойства следуют из соответствующих свойств ковариационной функции нестационар- ного процесса при замене τ = t1 − t2 .

В практических приложениях чаще всего используются ковариационные функции сле-

дующего вида:	R (τ) = σ2e−α|τ|
				,		(2.13)
	ξ	ξ
	R (τ) = σ2 (1 + α | τ |)e−α|τ| ,					(2.14)
	ξ	ξ
R (τ) = σ2		(1 + α | τ | +	α2τ2		)e−α|τ| ,	(2.15)
ξ	ξ			3
	R (τ) = σ2e−α2 τ2 .					(2.16)
	ξ	ξ

Графики ковариационных функций (2.13) – (2.16) для одних и тех же значений парамет- ров σ2ξ и α представлены на рисунке 2.7.

Корреляционная функция стационарного случайного процесса имеет следующие свойст-

ва:

1.rξ (τ) = rξ (−τ) .

2.rξ (0) = 1.

3.rξ (τ) ≤ 1.

Для стационарного случайного процесса корреляционная функция rξ (τ) обычно убывает

по модулю при увеличении τ . В связи с этим вводится понятие времени корреляции стацио- нарного случайного процесса. Временем корреляции τk стационарного случайного процесса

называется промежуток времени между двумя сечениями процесса, в течение которого кор- реляционная функция по модулю уменьшается до величины ε . Положительное число ε вы-

20