Sluchaynye_protsessy

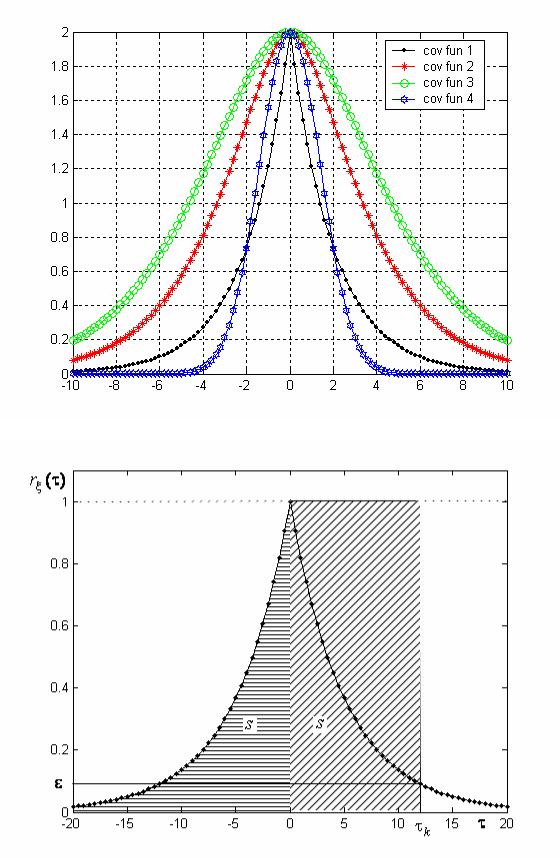
бирается из набора чисел 0,1; 0,05; 0,025 . Время корреляции отмечено на рис. 2.8 на при- мере корреляционной функции (2.13).

Рис. 2.7. Ковариационные функции стационарных случайных процессов

Рис. 2.8. Корреляционная функция (2.13) и время корреляции случайного процесса

21

Время корреляции определяется как решение относительно τ уравнения rξ (τ) = ε .

Иногда время корреляции определяется соотношением

∞0

τk = ò rξ (τ)dτ = ò rξ (τ)dτ .

0−∞

Вэтом случае время корреляции представляет собой длину основания прямоугольника еди-

ничной высоты, площадь которого равна площади под кривой корреляционной функции на действительной полуоси (рис. 2.8). Равные площади отмечены на рис. 2.8 символом s и раз- нонаправленной штриховкой.

2.7. Гауссовский (нормальный) случайный процесс

Случайный процесс ξ(t) называется гаусовским (нормальным), если все его конечномер-

ные распределения гауссовские, т. е. если его n -мерная плотность вероятности определяется

выражением

f

ξ

(x ,...,x

n

,t ,...,t

n

) =

1

exp(−

1

(X − A)T R−1(X − A)) ,

1

1

(2π)n | R |

2

где

AT = (aξ (t1),..., aξ (tn ))

– вектор математических ожиданий процесса

в моменты

t ,...,t

n

, X T

= (x ,..., x ) – вектор-строка аргументов плотности вероятности,

R = (R

),

1

1

n

i, j

i, j =

, – ковариационная матрица процесса,

R

1,n

– определитель ковариационной матри-

цы,

R−1 – обратная матрица. Элементы R

ковариационной матрицы процесса представля-

i, j

ет собой коэффициенты ковариации между сечениями процесса ξ(ti ) и ξ(t j ) , т. е.

o

o

Ri, j

= cov(ξ(ti ), ξ(t j )) = E(ξ(ti ) ξ(t j )) = Rξ (ti ,t j ).

Мы видим, что ковариационная матрица вычисляется по ковариационной функции случай- ного процесса: Ri, j = Rξ (ti ,t j ) .

22

3.СПЕКТРАЛЬНАЯ ТЕОРИЯ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ

3.1.Спектральная функция и спектральная плотность стационарного случайного про-

цесса с непрерывным временем

Пусть ξ(t) – непрерывный в среднем квадратичном стационарный случайный процесс и Rξ (τ) – его ковариационная функция. Характеристическое свойство ковариационной функ-

ции – неотрицательная определенность – в случае стационарного случайного процесса сво-

дится к соотношению

m m

å å R(tk - t j )zk z j ³ 0

k =1j=1

для любого конечного множества точек t j и любых чисел z j .

Относительно ковариационной функции Rξ (τ) справедлива следующая теорема Бохнера. Теорема. Функция Rξ (τ) неотрицательно определена тогда и только тогда, кода она мо- жет быть представлена в виде интеграла Фурье-Стилтьеса по некоторой вещественной не-

убывающей и ограниченной функции Sξ (ω) :

	∞
R(t) =	òe jωτdSξ (w) .	(3.1)

−∞

Теорему принимаем без доказательства.

Функция Sξ (ω) в формуле (3.1) называется спектральной функцией случайного процесса ξ(t) , а формула (3.1) называется спектральным представлением ковариационной функции. С точки зрения спектрального представления (3.1) не важно, как определить Sξ (ω) в точках разрыва. Обычно ее считают непрерывной справа, так что Sξ (ω) = Sξ (ω + 0) .

Формула обращения для преобразования (3.1) имеет вид:

Sξ (w2 ) - Sξ (w1) =	1	lim	c	e jω1τ - e jω2τ	Rξ (t)dt.
			ò
				jt
	2p c→∞ −c

Если спектральная функция абсолютно непрерывна, т.е. может быть представлена в виде

ω

Sξ (w) = ò sξ (l)dl ,

−∞

то функция sξ (ω) называется спектральной плотностью случайного процесса ξ(t) . Из по- следнего выражения получаем, что

sξ (w) =	d	Sξ (w).
	dw
Если существует спектральная плотность sξ (ω) , то
dSξ (ω) = sξ (ω)dω,
и вместо (3.1) получаем
∞
Rξ = ò e jωτ sξ (ω )dω ,			(3.2)

−∞

23

т.е. ковариационная функция может быть представлена как преобразование Фурье от спек- тральной плотности. Тогда спектральная плотность стационарного случайного процесса ξ(t) будет преобразованием Фурье от его ковариационной функции:

s	ξ	(ω) =	1	∞e− jωτ R (τ)dτ .		(3.3)
				ò	ξ
			2π −∞

Обратимся к спектральной плоскости (3.1) и исследуем её свойства. Так как по формуле

Эйлера

e− jωτ = cosωτ − jsin ωτ,

то

∞ R (τ)cos ωτdτ −

∞ R (τ)sin ωτdτ .

s

ξ

(ω) =

1

j

2π

ò

ξ

ò

ξ

−∞

2π −∞

Rξ (τ) второй интеграл в правой

В силу нечетности функции sin ωτ и четности функции

части последнего выражения будет равен нулю, и мы получим

s

ξ

(ω)=

1

∞R (τ)cosωτdτ.

(3.4)

ò ξ

2π −∞

Поскольку функции cos ωτ и

Rξ (τ) четные, то и спектральная плоскость

sξ (ω) будет

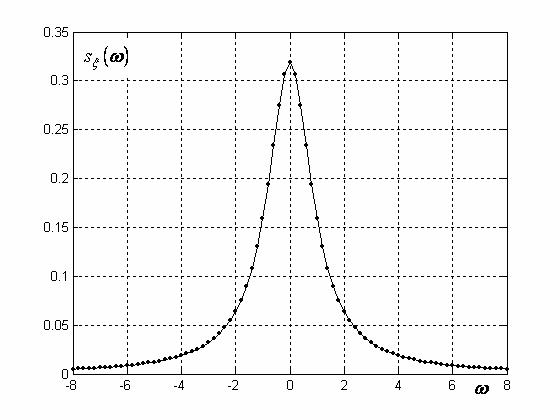
четной: sξ (− ω)= sξ (ω) (см. рис. 3.1).

Рис. 3.1 Спектральная плотность стационарного случайного процесса с ковариационной функцией (1.13)

Выясним физический смысл спектральной плотности. Для этого рассмотрим выражение

(3.3) при τ = 0:

24

Rξ (0)= ∞òsξ (w)dw.

−∞

Но Rξ (0) = sξ2 , где sξ2 – дисперсия процесса. Следовательно, площадь под кривой спек-

тральной плоскости равна дисперсии случайного процесса, или, иначе, спектральная плот- ность представляет собой распределение дисперсии процесса по оси частот. С другой сторо-

ны, sξ2	o	o
	= E(x2	(t)) . Если рассматривать x(t) как ток, протекающий в единичном сопротив-

o

лении, то x2 (t) будет представлять собой мгновенную (в момент времени t ) мощность про- o

цесса, а E(ξ2 (t)) – среднюю мощность процесса ξ(t). С этой позиции спектральную плот- ность можно трактовать как распределение средней мощности случайного процесса по час- тотным составляющим случайного процесса. Поэтому sξ (ω) иногда называют спектральной

плотностью мощности случайного процесса.

Пример. Найдем спектральную плотность процесса, имеющего ковариационную функцию вида Rξ (t) = s2ξe−α|τ| .

Решение. По определению спектральной плотности получим

s(w) = 1 ∞òs2e−α

ξ2p −∞ ξ

= 21p

= s2 e(α+ jω)τ

ξ

2p(a + jw)

0

∞

τ

e− jωτ dt=

1

òsξ2eατe jωτdt +

1

òsξ2e

−ατe− jωτdt =

0

2p −∞

∞

2p 0

1

òsξ2e(α+ jω)τdt +

òsξ2e−(α+ jω)τdt =

−∞

2p 0

0

sξ2

e−(α+ jω)τ

∞

sξ2 æ

1

1

ö

-

=

ç

+

÷ =

2p(a + jw)

ç

÷

−∞

0

2p è a - jw a + jwø

s

2a

=

ξ

.

p(a2 + w2 )

Эта функция приведена на рис. 3.1.

3.2 Спектральная функция и спектральная плотность стационарной случайной последовательности

Рассмотрим случайную последовательность ξ(iT ), которая образуется выборкой сечений случайного процесса с непрерывным временем ξ(t) в дискретные моменты времени iT , i =1,2,3..., T – период дискретизации (см. рис. 1.2). Ковариационная функция такой после-

довательности будет также определенной на дискретном множестве значений своих аргу- ментов. Если последовательность стационарная, то ее ковариационная функция образует по-

следовательность коэффициентов ковариаций Rξ (0T ), Rξ (± T ), Rξ (± 2T ), ...,

Rξ (± iT ),… , где

o o

Rξ (iT ) = E(x(kT )x(kT + iT )).

25

Относительно ковариационной функции Rξ (± kT ) может быть доказана теорема, аналогич- ная теореме Бохнера для процесса с непрерывным временем:

Теорема. Функция Rξ (kT ) неотрицательно определена тогда и только тогда, кода она может быть представлена в виде интеграла Фурье–Стилтьеса по некоторой вещественной неубывающей и ограниченной функции Sξ,T (ω):

	π / T
Rξ (kT ) =	ò e jωkT dSξ,T (w) , k = 0, ± 1, ± 2,... .	(3.5)

−π / T

Функция Sξ,T (ω) в данной формуле называется спектральной функцией случайной по- следовательности ξ(iT ), а формула (3.5) называется спектральным представлением кова- риационной функции Rξ (kT ). Спектральную функцию можно считать непрерывной справа

и удовлетворяющей условиям

p ö

æ p ö

S

æ

-

= 0,

S

= R

(0) .

ç

÷

ç

÷

ξ,T è

T ø

ξ,T

èT ø

ξ,T

Sξ,T (ω) абсолютно непрерывна на

é

p

,

pù

Если спектральная функция

ê-

ú

, т.е. может

T

быть представлена в виде

ë

T û

ω

Sξ,T (w) =

ò sξ,T (l)dl ,

то производная

−π / T

d

p

p

é

ù

sξ,T (w) =

Sξ,T (w), ê-

£ w £

ú

,

dw

T

T

ë

û

называется спектральной плотностью стационарной случайной последовательности ξ(iT ). Если существует спектральная плотность sξ,T (ω), то

dSξ,T (ω) = sξ,T (ω)dω,

и вместо (3.5) получаем

	π / T
Rξ (kT ) =	ò e jωkT sξ,T (w)dw.	(3.6)

−π / T

Так как это формула для коэффициентов ряда Фурье, то спектральная плотность стационар- ной случайной последовательности может быть представлена рядом Фурье:

T

∞

R (kT )e− jkωT

é-

p

p

ù .

s

ξ,T

(w) =

å

,

£ w £

2p k =−∞

ξ

ê

T

ú

ë

T û

Это ряд Фурье в комплексной форме. Если воспользоваться формулой Эйлера

e− jkωT = cos(kωT) − jsin(kωT) ,

то спектральную плотность можно записать в виде
s	ξ,T	(w) =	T	å∞ [R (kT )cos(kwT ) - R (kT )sin(kwT )].
				ξ	ξ
			2p k =−∞
Если учесть что синус – функция нечетная, а Rξ (kT)					– четная, то второе слагаемое в по-
следнем выражении оказывается равным нулю и

26

			T	∞	R (kT )cos(kwT ) .
s		(w) =		å
	ξ,T		2p k =−∞		ξ

Таким образом, спектральная плотность стационарной случайной последовательности пред- ставляет собой ряд Фурье по косинусам, т.е. является действительной четной функцией ар-

гумента ω . Если учесть, что функция Rξ (kT) четная, то можно записать

s	ξ,T	(w) =		T	(R (0) + 2R (T ) cos(wT ) + 2R (2T ) cos(wT ) + K).
				2p		ξ			ξ	ξ
Если, кроме того, ω = 0 , то получим
						T æ Rξ (0)				ö
		sξ,T	(0) =				ç			÷
						ç		2	+ Rξ (T ) + Rξ (2T ) + Rξ (3T ) +K÷.
						p è				ø

	T æ		R(0)		ö
sT (0) =		ç		+ R(T ) + R(2T ) + R(3T ) + K÷ .
			2
	π è				ø
				3.3. Белый шум
Случайный процесс	ξ(t) , спектральная плотность которого постоянна,
( sξ (ω)= c = const) называется белым шумом. Из формулы
				∞
			Rξ (0) =		òsξ (w)dw = sξ2
следует, что для белого шума				−∞
				∞	∞
		Rξ (0) = òcdw = c òdw = ¥ ,
				−∞	−∞

т. е. дисперсия (средняя мощность) равна бесконечности. Таких «бесконечно мощных» про- цессов в природе не существует. Но белый шум является хорошей математической идеали- зацией случайного процесса на входе некоторой динамической системы в случае, когда спек- тральная плотность процесса изменяется незначительно в полосе пропускания системы. На-

пример, входной случайный процесс со спектральной плотностью sξ (ω) , представленной на

рис. 3.2, можно считать белым шумом для системы с амплитудно-частотной характеристи- кой A(ω) .

Найдем ковариационную функцию белого шума:

R (t) =	∞ce jωτdw = c	∞e jωτdw = cd(t),
ξ	ò	ò
	−∞	−∞

где δ(τ) – известная дельта функция. Выражение d(t)= ∞òe jωτdw является одним из опре-

−∞

делений дельта функции. Случайный процесс с ковариационной функцией вида дельта функции называется некоррелированным. Это значит, что два сколь угодно близких сечения белого шума не коррелированны между собой. Итак, белый шум – это некоррелированный стационарный случайный процесс. Белый шум содержит в себе все частотные составляющие с равными амплитудами, подобно белому цвету. Этим объясняется название такого случай- ного процесса.

27

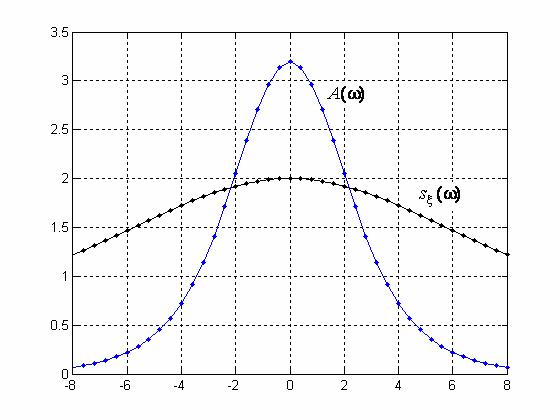
Рис. 3.2. Амплитудно-частотная характеристика A(ω) системы и спектральная плотность sξ (ω) входного случайного сигнала

28

4. НЕПРЕРЫВНОСТЬ, ДИФФЕРЕНЦИРУЕМОСТЬ И ИНТЕГРИРУЕМОСТЬ СЛУЧАЙНЫХ ПРОЦЕССОВ

4.1. Непрерывность случайного процесса

Понятие непрерывности случайного процесса x(t) отличается от понятия непрерывности неслучайной функции y(t) . Неслучайная функция y(t) называется непрерывной в точке t ,

если y(t + h) − y(t) → 0.

h→0

Для случайного процесса величина x(t + h) - x(t) является случайной величиной, и тре-

бовать выполнения условия ξ(t + h) − ξ(t) → 0 для случайной величины без дополнитель- h→0

ных условий не имеет смысла. Для случайных процессов существуют специальные опреде- ления непрерывности.

Случайный процесс x(t) называется непрерывным в среднем квадратичном, если прира- щение процесса x(t + h) - x(t) сходится к нулю в среднем квадратичном при h → 0 , т. е.

если выполняется условие

E((ξ(t + h) − ξ(t))2 ) → 0 .	(4.1)
h→0

Данное определение можно записать в виде

l.i.m.ξ(t + h) = ξ(t) .

h→0

Случайный процесс x(t) называется непрерывным с вероятностью 1, если

P(ξ(t + h) → ξ(t)) =1.

h→0

Непрерывность с вероятностью 1 означает непрерывность каждой реализации процесса в точке t .

О непрерывности процесса в среднем квадратичном можно судить по его вероятностным характеристикам.

Теорема. Случайный процесс x(t) непрерывен в среднем квадратичном в точке t T то- гда и только тогда, когда его функция математического ожидания aξ (t) = E(ξ(t) непре- рывна в точке t T и ковариационная функция Rξ (t1,t2 ) непрерывна в точке (t,t) (на диагонали области определения).

Докажем достаточность этих условий, т. е. докажем, что если aξ (t) = E(ξ(t) непрерывна

в точке

t и R

(t ,t

2

) непрерывна в точке t

= t

2

= t , то выполняется условие (4.1). Рас-

ξ

1

1

смотрим математическое ожидание квадрата приращения процесса

E((ξ(t + h) − ξ(t))2 ) = D(ξ(t + h) − ξ(t)) + E2 (ξ(t + h) − ξ(t)) =

= D(ξ(t + h)) + D(ξ(t)) − 2cov(ξ(t + h), ξ(t)) + (aξ (t + h) − aξ (t))2 =

= R

(t + h,t + h) + R (t,t) − 2R

(t + h,t) + (a

ξ

(t + h) − a

ξ

(t))2 ,

(4.2)

ξ

ξ

ξ

где символом D(×) обозначена дисперсия. Из последнего выражения видно, что при выпол- нении условий теоремы правая часть выражения (4.2) сходится к нулю при h → 0 , т.е.

E((ξ(t + h) − ξ(t))2 ) → 0 , что требовалось доказать. h→0

29

Докажем теперь необходимость, т.е. если выполняется условие (4.1), то aξ (t) непрерыв- на в точке t , а Rξ (t1,t2 ) непрерывна в точке t1 = t2 = t . Будем исходить из выражения

(4.2). В этом выражении

Rξ (t + h,t + h) - 2Rξ (t + h,t) + Rξ (t,t) ³ 0 .

Это следует из свойства неотрицательной определенности ковариационной функции

Дадим интерпретацию этой теоремы для стационарного случайного процесса: стационар- ный случайный процесс ξ(t) непрерывен в среднем квадратичном тогда и только тогда, ко-

гда его ковариационная функция Rξ (t) непрерывна в точке τ = 0 . Действительно для ста- ционарного процесса aξ (t) = const , т. е. математическое ожидание непрерывно в любой точке, а непрерывность ковариационной функции Rξ (t1,t2 ) в точке (t,t) сводится к непре-

рывности функции Rξ (t) = Rξ (t1 - t2 ) в нуле.

Пример. Является ли непрерывным в среднем квадратичном случайный процесс с кова- риационной функцией Rξ (t) = s2ξe−α τ ?

Решение. Поскольку ковариационная функция Rξ (τ) непрерывна в точке τ = 0, то по

теореме о непрерывности в среднем квадратичном стационарного процесса делаем вывод, что процесс непрерывен в среднем квадратичном.

4.2. Дифференцируемость случайного процесса

Рассмотрим дифференцируемость случайного процесса в среднем квадратичном. Случайный процесс ξ(t) называется дифференцируемым в среднеквадратичной точке t ,

если величина	ξ(t + h) − ξ(t)					′	в среднем квадратич-
	h		сходится к некоторому пределу ξ (t)
ном, т. е.
	æ	æ x(t + h) - x(t)		ö2	ö	® 0 .	(4.2)
	Eç	ç	h	- x¢(t)÷	÷
	ç	è		ø	÷h→0
	è				ø

Предел ξ′(t) называется производной в среднем квадратичном процесса ξ(t) в точке t .

О дифференцируемости случайного процесса в среднем квадратичном можно судить по его математическому ожиданию и ковариационной функции.

Теорема. Случайный процесс ξ(t) дифференцируем в среднем квадратичном в точке t тогда и только когда, когда его функция математического ожидания aξ (t) дифференцируе-

ма в точке t и ковариационная функция Rξ (t1,t2 )					дифференцируема в точке (t, t) (на диа-
гонали области определения).
Будем доказывать сходимость к нулю величины
æ	æ x(t + h) - x(t)		-	x(t + k) - x(t) ö2			ö
Eç	ç	h			k	÷	÷ ® 0 .
ç	è					ø	÷h,k →0
è							ø

30