Sluchaynye_protsessy

Если эта величина сходится, то на основании критерия Коши сходимости в среднем квадра- тичном [ ] мы сможем утверждать, что выполняется сходимость (4.2). Как и раньше, найдём

математическое ожидание квадрата случайной величины

= Dæç x(t +

è

- æ x(t

2covç

è

æ

æ x(t + h) - x(t)

-

x(t + k) - x(t) ö

2 ö

=

Eç

ç

h

k

÷

÷

ç

è

ø

÷

h)- x(t)

è

ø

-

x(t + k) - x(t) ö

+

æ x(t + h) - x(t)

-

x(t + k) - x(t) ö

=

h

k

÷

E2ç

h

k

÷

ø

è

ø

=

æ x(t + h) - x(t) ö

æ x(t + k) - x(t) ö

-

Dç

h

÷

+ Dç

k

÷

è

ø

è

ø

+ h) - x(t) x(t + k) - x(t) ö

æ aξ (t + h) - aξ

(t)

aξ (t + k) - aξ (t) ö2

,

ç

-

÷

h

k

÷ + ç

h

k

÷ .

ø

è

ø

Последующие преобразования проиллюстрируем на примере одного слагаемого:

æ x(t + h) - aξ (t) ö				Rξ (t + h,t + h) - Rξ (t,t) - 2Rξ (t + h,t)
ç		÷	=			.
					2
Dç	h	÷		h
è		ø

Видно, что это выражение есть определение смешанной производной второго порядка от ко- вариационной функции в точке (t, t), если только эта производная существует. Таким обра- зом, если производная существует, то

æ x(t + h) - aξ (t) ö				¶2
ç		÷	®		Rξ (t1,t2 )			.
Dç	h	÷		¶t1¶t2
è		øh→0				t1	=t2	=t

Выполнив аналогичные преобразования для остальных слагаемых, можно показать, что

æ

æ x(t + h) - x(t)

-

x(t + k) - x(t) ö2

ö

®

0 ,

Eç

ç

h

k

÷

÷

ç

è

ø

÷h,k →0

è

ø

если только существуют производные

d

a

ξ

(t),

¶2

R (t ,t

)

существуют.

dt

¶t ¶t

ξ 1

2

1

2

t1 =t2 =t

4.3. Дифференцируемость стационарного случайного процесса

Теорема. Стационарный в широком смысле процесс ξ(t) дифференцируем в среднем

квадратичном тогда и только тогда, когда существует вторая производная его ковариацион- ной функции в нуле, т. е. существует

dt22 Rξ (t) τ=0 .

d

Действительно, так как процесс стационарный, то aξ (t) = c = const, т. е. математическое ожидание дифференцируемо в любой точке t . Ковариационная функция стационарного про- цесса обладает свойством Rξ (t1,t2 ) = Rξ (t1 − t2 ) = Rξ (τ) . В таком случае

31

¶2		¶2			¶		æ	¶		ö
							ç			÷
¶t ¶t		Rξ (t1,t2 ) = ¶t ¶t			Rξ (t1 - t2 ) = ¶t			¶t			=
	2			2			ç		2	Rξ (t)÷
1		1			1		è			ø

¶ æ

¶R (t)

¶t ö

¶ æ

¶R (t) ö

¶2

ç

ξ

÷

ç

ξ

÷

= ¶t

¶t ¶t

= - ¶t

¶t

= - ¶t2 Rξ (t) ,

ç

2

÷

ç

÷

1

è

ø

1

è

ø

и условие существования смешанной производной второго порядка на диагонали для неста- ционарного процесса сводится к условию существования производной второго порядка в ну- ле для стационарного процесса.

Пример. Дифференцируем ли в среднем квадратичном случайный процесс с ковариаци- онной функцией вида Rξ (t) = s2ξe−α τ ?

Решение. Перепишем ковариационную функцию в виде

Rξ (t)

Дифференцирование дает

			ì		2	e	−ατ	,t ³ 0,
				s	ξ
= sξ2e−α		τ		ï
				= í	2eατ ,t < 0.
				ïs
			î		ξ

d		ì	2	−ατ	, t ³ 0,
		ï- asξe
	R (t) = í
dt
	ξ	ïas2eατ ,t < 0.
		î	ξ

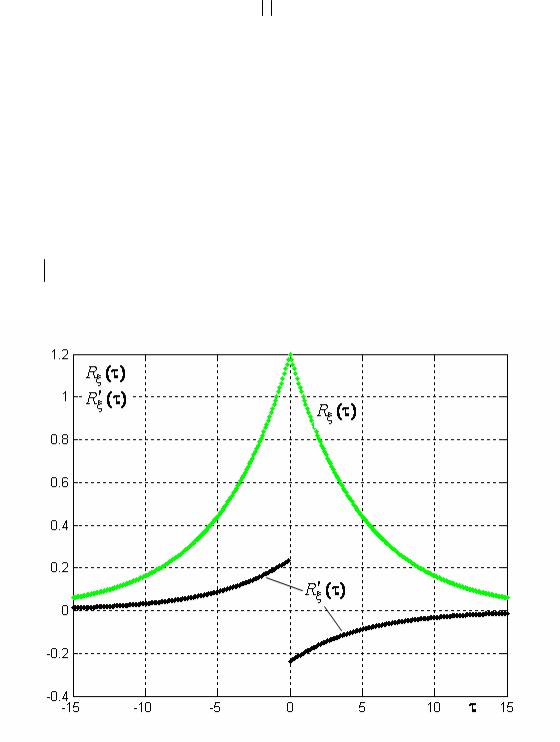
Ковариационная функция и ее производная представлены на рис. 4.1. Мы видим, что произ- водная Rξ′ (τ) в точке τ = 0 имеем разрыв первого рода, следовательно, вторая производная

R′′(τ) τ=0 в этой точке не существует, и такой процесс не дифференцируем в среднем квад- ратичном.

32

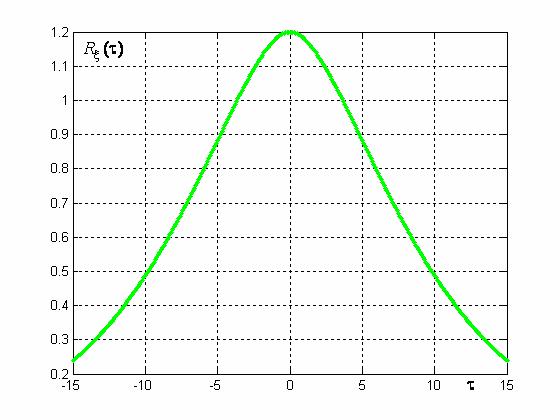
Рис. 4.1. Ковариационная функция (1.13) и ее производная

Пример 2: Дифференцируем ли в среднем квадратичном стационарный случайный про-

цесс с ковариационной функцией вида

R (t) = s2		(1 + a | t |)e−α|τ|	?	(4.3)
ξ	ξ

Решение. Перепишем ковариационную функцию в виде

				ì	2	(1+ at)e	−ατ	,t ³ 0,
2			−α|τ|	s	ξ
	(1	+ a | t |)e		ï
Rξ (t) = sξ				= í		(1- at)eατ ,t < 0.
				ïs2
				î	ξ

′

Дифференцируя эту функцию, получим Rξ (τ)

ì

2

2

−ατ

, t ³ 0,

¢

ï- a

sξte

(t) = í

Rξ

2s2teατ ,t < 0.

ï- a

î

ξ

ì

2

2

(1

- at)e

−ατ

, t ³ 0,

¢¢

ï- a

sξ

2

2

- a | t |)e

−α|τ|

(t) = í

= -a

(1

Rξ

2s2

(1

+ at)eατ ,t < 0,

sξ

ï- a

î

ξ

Мы видим, что вторая производная R′′(τ) в точке τ = 0 существует и равна

.

- a2sξ2 . Сле-

довательно, случайный процесс с такой ковариационной функцией дифференцируем в сред- нем квадратичном. Ковариационная функция (4.3) изображена на рис. 4.2, а ее производные

– на рис. 4.3.

Рис. 4.2. Ковариационная функция (4.3)

33

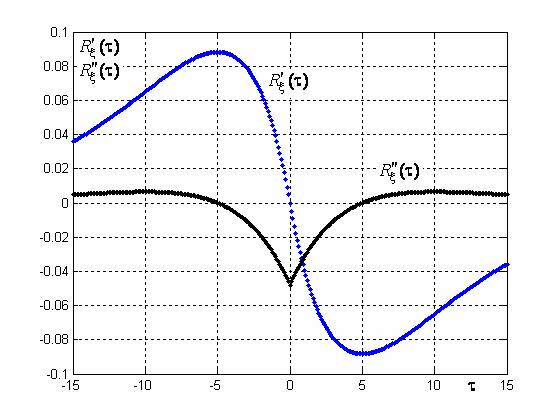
Рис. 4.3. Первая и вторая производные ковариационной функции (4.3)

4.4. Производная в среднем квадратичном случайного процесса

Пусть ξ′(t) – производная в среднем квадратичном процесса ξ (t), aξ (t) – математиче- ское ожидание процесса ξ(t) , Rξ (t1,t2 ) – ковариационная функция процесса. Нас интере- суют математическое ожидание aξ (t) = E(ξ′(t)) и ковариационная функция Rξ′ (t1,t2 )

производной ξ′(t) этого процесса.

Теорема. Математическое ожидание и ковариационная функция производной в среднем

квадратичном случайного процесса определяются выражениями

′

d

′

aξ′ (t) = aξ (t) =

dt

aξ (t),

∂2

R

(t ,t

2

) =

R (t ,t

2

) .

ξ′

1

∂t1dt2

ξ

1

Докажем эту теорему. Для математического ожидания производной получим

′

ξ(t + h) − ξ(t)

) .

aξ′ (t) = E(ξ (t)) = E(lim

h

h→0

Поскольку сходимость в среднем квадратичном обладает тем свойством, что символы E и

l.i.m. перестановочны [ ], то

αξ

(t + h) − αξ (t)

aξ′ (t) = lim E(

ξ(t + h) − ξ(t)

) = lim (

) =

d

aξ (t) .

h

h

dt

h→0

h→0

Итак, мы доказали, что

34

E(dtd ξ(t)) = dtd E(ξ(t)) .

Мы видим, что операции E и d / dt в среднем квадратичном также перестановочны. Вос- пользуемся этим свойством для доказательства утверждения теоремы относительно ковариа- ционной функции производной:

d

o

d

o

∂ ∂

o

o

∂

2

R

(t ,t

) = E(

ξ(t )

ξ(t

)) = E(

ξ(t ) ξ(t

)) =

R (t ,t

) .

dt

dt

∂t ∂t

∂t dt

ξ′

1

2

q

1

2

2

2

1

2

2

ξ

1

2

1

1

Теорема доказана.

Теорема. Математическое ожидание и ковариационная функция производной в среднем

квадратичном стационарного случайного процесса определяются выражениями

aξ′ (t) = 0 ,

Rξ′ (τ) = − d 2 Rξ (τ) .

dτ2

Результат этой теоремы вытекает из предыдущей теоремы. Действительно, для стацио-

нарного случайного процесса aξ (t) = const, поэтому всегда

d

aξ (t) = 0. Кроме того, для

dt

стационарного

случайного

процесса

Rξ (t1,t2 ) = Rξ (t1 − t2 ) = Rξ (τ)

и

∂2

R (t ,t

) = −

∂2

R (τ) . Теорема доказана.

∂t dt

∂τ2

2

ξ 1

2

ξ

1

Из последней теоремы следует, что производная в среднем квадратичном стационарного случайного процесса так же является стационарным случайным процессом, поскольку ее ма- тематическое ожидание не зависит от времени (равно нулю) и ковариационная функция за- висит лишь от одного аргумента τ .

4.5. Интегрируемость случайного процесса

Интеграл Римана от любой неслучайной функции определяется как предел соответст- вующей интегральной суммы Римана. Интеграл от случайного процесса можно определить как предел в среднем квадратичном такой же интегральной суммы Римана.

Дадим определение интеграла в среднем квадратичном вида

	b
	I = ò g(t)ξ(t)d(t) ,
где ξ(t)	a
	– случайный процесс, g(t) – детерминированная функция. Для этого рассмотрим
интегральную сумму Римана
	m	−ti ) , t' (ti ,ti+1) .
	sm = å g(t')ξ(t')(ti+1
	i =1
Предел	в среднем квадратичном интегральной суммы sm при m → ∞ и

max(ti+1 − ti ) → 0 , если он существует, называется интегралом в среднем квадратичном и обозначается обычным способом:

b

I = ò

a

g(t)ξ(t)dt =	l.i.m. sm .
	m→∞
	max(t i+1−ti )→0

35

Теорема. Если случайный процесс ξ(t) и детерминированная функция g(t) таковы, что

существуют интегралы

b

P = ò g(t)aξ (t)dt ,

a

b b

Q = ò ò g(t1)g(t2 )Rξ (t1,t2 )dt1dt2 ,

a a

где aξ (t) – математическое ожидание случайного процесса ξ(t) , Rξ (t1,t2 ) – ковариацион-

ная функция случайного процесса ξ(t) , то данный случайный процесс интегрируем в сред- нем квадратичном, причем

			æb	ö
			ç	÷	,
	P = E(I ) = Eç ò g(t)x(t)dt ÷
			èa	ø
	2	æ	æb	ö	2 ö
		ç	ç	÷	÷
	Q = E(I ) = Eç				÷.
			ç ò g(t)x(t)dt ÷
		è	è a	ø	ø
	Теорема. Стационарный случайный процесс ξ(t)			интегрируем в среднем квадратичном

тогда и только тогда, когда существуют интегралы

b

P = ò g(t)x(t)dt ,

a

Q = òò g(t1)g(t2 )Rξ (t1 - t2 )dt1dt2 ,

где Rξ (t1 − t2 ) = Rξ (τ) – ковариационная функция стационарного случайного процесса. Данная теорема вытекает из предыдущей.

4.6. Интеграл от случайного процесса с переменным верхним пределом

На практике очень часто приходиться иметь дело с интегралом вида

t

η(t) = ò g(v)ξ (v)dv ,

a

где ξ (v) – случайный процесс, g(v) – неслучайная функция. Этот интеграл является функ- цией верхнего предела, т. е. случайным процессом η(t) . Будем понимать этот интеграл в

среднем квадратичном смысле.

Теорема. Математическое ожидание и ковариационная функция интеграла в среднем квадратичном с переменным верхним пределом от случайного процесса ξ (t) определяются

выражениями

t

aη (t) = E(η(t)) = ò g(v)aξ (v)dv ,

a

t1 t2

Rη (t1, t2 ) = ò ò g(v1)g(v2 )Rξ (v1, v2 )dv1dv2 ,

a a

36

где aξ (t), Rξ (t1,t2 ) – математическое ожидание и ковариационная функция процесса ξ (t).

Данная теорема является интерпретацией предыдущей теоремы в случае, когда верхний предел интегрирования является переменным.

Теорема. Математическое ожидание и ковариационная функция интеграла в среднем квадратичном с переменным верхним пределом от стационарного случайного процесса ξ (t)

определяются выражениями

t

aη (t) = E(η(t)) = ò aξ g(v)dv ,

a

t1 t2

Rη (t1, t2 ) = ò ò g(v1 )g(v2 )Rξ (v1 − v2 )dv1dv2 .

a a

Эта теорема является частным случаем предыдущей. Из этой теоремы видно, что интеграл

в среднем квадратичном с переменным верхним пределом от стационарного случайного процесса стационарным не является, так как его математическое ожидание не является по-

стоянным, и ковариационная функция зависит от двух аргументов t1 , t2 .

37

5. ДИНАМИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

5.1. Прохождение нестационарного случайного процесса через линейную стационарную динамическую систему

Пусть процесс ξ(t) с математическим ожиданием aξ (t) и ковариационной функцией

Rξ(t1,t2) подается на вход линейной динамической системы. Нас интересуют математиче-

ское ожидание aη (t) и ковариационная функция Rη (t1,t2) процесса η(t) на выходе ди-

намической системы.

Любая стационарная динамическая система описывается импульсной переходной функ- цией k(t) , причем, для физически реализуемых динамических систем k(t) = 0 при t < 0 . Импульсная переходная функция k(t) является реакцией системы на входное воздействие в

виде дельта-функции δ(t) . Выходной сигнал динамической системы определяется как ин-

теграл свертки

∞

η(t) = ò k(t)ξ(t − τ)dτ .

0

Будем считать систему устойчивой, т. е. будем считать, что этот интеграл существует в среднем квадратичном.

Теорема. Для устойчивой стационарной динамической системы математическое ожидание и ковариационная функция выходного процесса η(t) , а также взаимная ковариационная

функция входного и выходного процессов определяются выражениями

∞

aη (t) = ò k(t)αξ (t − τ)dτ,

0

∞∞

Rη (t1,t2 ) = ò ò k(v)k(w)Rξ (t1 − v,t2 − w)dvdw ,

0 0

∞

Rξ,η(t1,t2 ) = ò k(τ)Rξ (t1,t2 − τ)dτ ,

0

где aξ (t) , Rξ(t1,t2) – математическое ожидание и ковариационная функция входного про- цесса.

5.2. Прохождение стационарного случайного процесса через линейную стационарную динамическую систему

Теорема. Если входной процесс ξ(t) устойчивой стационарной динамической системы стационарен, то математическое ожидание и ковариационная функция выходного процесса η(t) , а также взаимная ковариационная функция входного и выходного процессов опреде-

ляются выражениями

∞
aη (t) = αξ òk(t)dt = const ,	(5.1)
0

38

	∞∞
Rη (t1,t2 ) =	ò ò k(v)k(w)Rξ (t1 − v − t2				+ w)dvdw = Rη(t1	− t2 ),	(5.2)
	0 0	∞
Rξ,η(t1,t2 ) =		ò k(τ)Rξ (t1	− t2	+ τ)dτ = Rξ,η(t1 − t2 ) .
		0

Мы видим, что выходной процесс в этом случае является стационарным, а входной и выход- ной – стационарно связанными, поскольку математическое ожидание выходного процесса не зависит от времени, ковариационная функция выходного процесса зависит только от разно-

сти t1 − t2 и взаимная ковариационная функция входного и выходного процессов зависит только от разности t1 − t2 .

В случае стационарной системы и стационарного входного процесса удобнее оперировать не ковариационными функциями, а спектральными плотностями, и не импульсной переход- ной функцией, а частотной передаточной функцией системы.

Частотной передаточной функцией стационарной динамической системы называется пре- образование Фурье от ее импульсной переходной функции:

∞

W ( jω) = ò k(t)e− jωt dt .

0

Пусть Sξ (ω) – спектральная плотность входного процесса ξ(t) , а Sη (ω) – спектральная плотность выходного процесса η(t) . Найдем Sη (w) и aη . Из определения передаточной

функции получаем, что

∞

W (0) = òk(t)dt .

0

Подставляя это выражение в выражение (5.1), получим, что

aη = w(0)aξ .

Чтобы найти выражение для спектральной плотности Sη (ω) , найдем преобразования Фурье от обеих частей равенства (5.2):

S	η	(ω) =	1	∞e− jωψ	∞∞k(υ)k(ω)R (τ − υ + ω)dτdυdω =
				ò	ò ò	ζ
			2δ 0		0 0

= W ( jω)W (− jω)Sξ (ω).

Если учесть, что W ( jω)W (− jω)= W (jω)2 , то

Sη (ω)= W ( jω)2 Sξ (ω).

Пример. Пусть система описывается дифференциальным уравнением:

	dη(t)		+ Tη(t)= kξ(t) и Sξ (ω) =	α
	dt			(α2 + ω2 )π

Найдем спектральную плотность на выходе такой системы. Заменяя оператор дифференци- рования символом p , получим

pη(p)+ Tη(p)= kξ(p), (p + T )η(p)= kξ(p).

Отсюда W (p)=	k	, W (0)=	k	, так что
	T + p
		T

39

aη =

k

aξ ,

T

k 2α

Sη (ω)=

k

k

α

=

.

(T + jω) (T − jω) π(α

2 + ω2 )

π(T 2

+ ω2 )(α2

+ ω2 )

40