51. Основные теоремы теории вероятностей. Формула полной вероятности. Формула Байеса.

1) Сложение Р(А+В) = Р(А)+Р(В) – для совмест. Событий

Р(А+В) = Р(А)+Р(В) – Р(АВ) – для несовм.

2) Умножение примен. В предположении, что событие А уже произошло. Р(АВ) = Р(А)* Р(В/А)

Формула полной вероятности: примен.для полной группы событий. Здесь ввод-ся понитие ГИПОТЕЗА (Н) Н₁, Н₂Нn – гипотеза события 1, 2 , н .

Формула Байеса: , где- вероятность гипотезы А,— вероятность гипотезы A при наступлении события B.— вероятность наступления события B при истинности гипотезы A;— полная вероятность наступления события B.

52. Случайные величины. Непрерывные и дискретные случайные величины. Распределение случайной величины. Интегральная и дифференциальная функции распределения.

СВ- это измеримая функция, заданная на каком-либо вероятностном пространстве.

Примеры случайных величин:

1) число попаданий при трех выстрелах;

2) число вызовов, поступавших на телефонную станцию за сутки;

3) частота попадания при 10 выстрелах.

Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.

Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.

Существуют случайные величины другого типа, например:

1) абсцисса точки попадания при выстреле;

2) ошибка взвешивания тела на аналитических весах;

3) скорость летательного аппарата в момент выхода на заданную высоту;

4) вес наугад взятого зерна пшеницы.

Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще – границы неопределенные, расплывчатые.

Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами. Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

53. Математическое ожидание и дисперсия. Интегральная и дифференциальная функции распределения. Полигон и гистограмма.

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: M(X) = x1p1 + x2p2 + ... + xnpn

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду

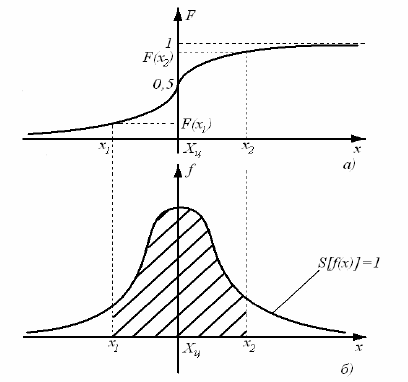Интегральной функцией распределения называют функцию , определяющую для каждого значения вероятность того, что случайная величина примет значение, меньшее , Рис. 3. Интегральная (а) и дифференциальная (б) функции распределения случайной величины Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина x_i в i -м опыте принимает значение, меньшее х. Она имеет следующие свойства: 1) неотрицательная, т.е. F(x)<0; 2) неубывающая 3) диапазон ее изменения: от 0 до Дифференциальной функцией распределения называется 1-я производная от интегральной функции распределения .

Полигон (для дискретной случайной величины) - ломаная, соединяющая точки (х_i, n_i — полигон частот или точки (х_i, w_i) — полигон относительных частот.

Полигон частот:

Гистограмма — ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются отрезки длиной x_i-x_i-1.

54. Повторение опытов и распределение Бернулли.Предположим, что несколько одинаковых машин в одних и тех же условиях перевозят груз. Любая машина может выйти из строя при этих перевозках. Пусть вероятность выхода из строя одной машины не зависит от выхода из строя других машин. Это значит, что рассматриваются независимые события (испытания). Вероятности выхода из строя каждой из этих машин примем одинаковыми ().

Пусть, в общем случае, производится независимых испытаний. Ставится задача определения вероятности того, что ровно в испытаниях наступит событие , если вероятность наступления этого события в каждом испытании равна . В случае с машинами это могут быть вероятности выхода из строя ровно одной машины, ровно двух машин и т.д.Определим вначале вероятность того, что в первых испытаниях событие наступит, а в остальных испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий,где .Так как рассматривалась только одна из возможных комбинаций, когда событие произошло только в первых испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из элементов по , т.е. .