Matematika

Государственное автономное образовательное учреждение высшего профессионального образования города Москвы

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ИНДУСТРИИ ТУРИЗМА

ИМЕНИ Ю.А.СЕНКЕВИЧА (ГАОУ ВПО МГИИТ имени Ю.А. Сенкевича)

Кронштадтский б-р, д. 43А, Москва, Россия, 125499, тел.: [phone]; факс: [phone]

E-mail:[e-mail], http://www.mgiit.ru

КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И МАТЕМАТИКИ

«МАТЕМАТИКА»

Методические указания и контрольные задания для студентов заочной формы обучения

по специальности 101100.62 «Гостиничное дело»

Задачи курса

1.Дать студентам сведения о современных математических методах, использующихся в математическом моделировании экономических процессов.

2.Ознакомить студентов с понятиями и основными фактами аналитической геометрии, математического анализа, линейной алгебры, линейного программирования, теории вероятностей и математической статистики.

3.Продемонстрировать эффективность применения изучаемых математических методов в туристической индустрии.

4.привить навыки самостоятельного изучения литературы по данной дисциплине и ее приложениям.

Отсюда вытекает необходимость изучения: элементов линейной алгебры, элементов аналитической геометрии, элементов дифференциального и интегрального исчисления, способов отбора и использования статистических данных на основе теории вероятностей.

Изложение и изучение данного курса опирается на базовые знания студентов, полученные ими в предшествующее время в школьном курсе математики. Из этого курса следует выделить свойства степеней и дробей, логарифмические и показательные функции, тригонометрию, геометрию, начала анализа. Студент должен знать основные понятия, свойства, формулы из этих разделов школьной математики и уметь использовать их при решении задач.

Изучение математики направлено на развитие логического и алгоритмического мышления студентов, освоение ими приемов решения математически формализованных задач, выработку умения самостоятельно проводить анализ прикладных задач и расширять в случае необходимости свои математические знания.

Требования к результатам освоения дисциплины В результате изучения дисциплины студент должен:

знать: фундаментальные разделы математики, необходимые для логического осмысления и обработки информации в профессиональной деятельности;

уметь: применять математические методы при решении практических задач в туристской деятельности;

владеть: математическими знаниями и методами, математическим аппаратом, необходимым для профессиональной деятельности в индустрии туризма;

В процессе изучения курса студенты выполняют одну контрольную работу, содержащую восемь задач, и сдают экзамен по утверждённым в установленном порядке билетам.

Задания для контрольной работы

Каждый студент должен решить 8 задач своего варианта. Номер варианта совпадает с последней цифрой учебного номера (шифра) студента. Например, для варианта №6 следует решить задачи №№ 6, 16, 26, 36, 46, 56, 66, 76; для варианта №0 следует решить задачи №№ 10, 20,

30, 40, 50, 60, 70, 80.

1–10. Даны вершины треугольника АВС.

Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.

2

1.	А (–5; 0),	В (7; 9),	C (5; –5).
2.	A (–7; 2),	B (5; 11),	С (3; –3).
3.	А (–5; –3),	В (7; 6),	C (5; –8).
4.	А (–6; –2),	В (6; 7),	C (4; –7).
5.	А ( –8; –4),	В (4; 5),	C (2; –9).
6.	А (0; –1),	В (12; 8),	С (10; –6).
7.	А (–6; 1),	В (6; 10),	С (4; –4).
8.	А (–2; –4),	В (10; 5),	С (8; –9).
9.	А (–3; 0),	В (9; 9),	С (7; –5).
10. А (–9; –2),		В (3; 7),	С (1; –7).

11–20. Решить данную систему уравнений с помощью формул Крамера. Сделать проверку полученного решения.

5х 8 у z 9,

11.х 2 у 3z 1,2x 3y 2z 5.

3х 2 у z 5, 13. 2х 3у z 1,

2x y 3z 11.

х 3у 2z 3, 15. 2х 5у 3z 4,

5x 6 y 2z 0.

х у 2z 1,

17.2х у 2z 4,4x y 4z 2.

3х	у	z 4,
19. 2х 5 у 3z 17,
	у	z 0.
x

х 2 у z 4,

12.3х 5 у 3z 1,2х 7 у z 8.

х 2 у 4z 31,

14.5х у 2z 29,3x y z 10.

2х

у

z 4,

16.3х 4 у 2z 11,3x 2 y 4z 11.

		3х у	5,
18.	2х у		z 0,
		2x y 4z 15.
		х у	z 2,
20.	2х у 6z 1,
	3x 2 y		8.

21–30. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.

х у 3z 0,

21.3х 2 у 2z 1,х у 5z 2.

2х 3у z 1, 22. х у 4z 0 ,

4х 5 у 3z 1.

3

	3х 2 у z 5,		х	4 у 2 5,
23.		х 3у 2z 2,	24. 4	х у 3z 3,
	5х 2 у 4z 7.		2	х 3у 4z 1.
	2х 4 у 3z 2,		х 2 у 3z 1,
25.		х у 2z 0,	26. 2	х 3у z 7,
	3х 2 у z 5.		4	х у 2z 0.
	3х у 4z 2,			3х 3у 2z 4,
27.		х 2 у 3z 7,		28. 2х у 3z 1,
	5х 3у 2z 8.			х 2 у 5z 1.
	4х у 3z 1,		2х у 3z 1,
29.	3х 2 у 4z 8,		30. х 2 у 5z 9,
	2х 2 у 4z 0.		4х 3у 2z 4.

31-40. Исследовать функцию y = f(x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f(x) на отрезке [a, b].

31.	y 2x3		9x2	12x 5,	a = 1 ,	b = 3
32.	y x3	6x2 9x 1,			a = 1 ,	b = 2
33.	y x3	3x2 9x 10,			a = 2 ,	b = 3
34.	y x3	3x2 9x 10,			a = 1 ,	b = 2
35.	y x3 6x2 9x 2,				a = 0 ,	b = 4
36.	y 2x3		3x2	12x 5,	a= 2 ,	b= 3
37.	y 2x3		3x2	12x 8,	a = 3 ,	b = 0
38.	y 2x3 9x2 12x 7,				a = 3 ,	b = 1
39.	y 2x3		15x2 36x 32,		a = 1 ,	b = 4
40.	y 2x3		3x2	36x 20,	a = 1 ,	b = 4

41 50. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.

41.	y 2x2 ,	y 2x 4.
42.	y x2 ,	y x 2.

4

	43.	y 3x2 ,						y x 4.
	44.	y		1		x2	,	y x 3.
				4
	45.	y		1		x2	,	y 3x 8.
				2
	46.	y		1	x2		,	y 3x 12.
				3
	47.	y 4x2 ,						y 2x 2.
	48.	y		1		x2	,	y	1	x 2.
				4				2
	49.	y 4x2 ,						y 2x 6.
	50.	y x2 ,						y x 3.

51–60. В ящике содержится n одинаковых, тщательно перемешанных шаров, причем k из них – красные, l – синие и m – белые. Наудачу вынимается один шар. Найти вероятность того, что вынутый шар

а) синий, б) белый, в) цветной.
51. n = 8,	k = 3,	l = 3,	m = 2.
52. n = 9,	k = 4,	l = 1,	m = 4.
53. n = 10, k = 3,		l = 5,	m = 2.
54. n = 11, k = 5,		l = 3,	m = 3.
55. n = 12, k = 4,		l = 6,	m = 2.
56. n = 8,	k = 1,	l = 5,	m = 2.
57. n = 9,	k = 3,	l = 4,	m = 2.
58. n = 10, k = 2,		l = 7,	m = 1.
59. n = 11, k = 2,		l = 4,	m = 5.
60. n = 12, k = 3,		l = 5,	m = 4.

61–70. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения.

61.

xi	1	3	5	7
pi	0,2	0,1	0,4	0,3

5

62.

xi	2	4	6	8
pi	0,5	0,1	0,3	0,1

63.

xi	2	3	5	7
pi	0,1	0,2	0,3	0,4

64.

xi	1	2	3	4
pi	0,6	0,1	0,1	0,2

65.

xi	10	12	15	20
pi	0,3	0,2	0,1	0,4

66.

xi	5	10	15	20
pi	0,1	0,3	0,1	0,5

67.

xi	10	15	20	25
pi	0,1	0,2	0,4	0,3

6

68.

xi	2	4	6	8
pi	0,2	0,1	0,4	0,3

69.

	xi	2	4	5	6
	pi	0,6	0,2	0,1	0,1
70.
	xi	3	4	6	7
	pi	0,3	0,2	0,4	0,1

71–80. Известны математическое ожидание a и среднеквадратическое отклонение нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал ( ; ).

71. a = 11,	= 5,	= 5,	= 10.
72. a = 10,	= 4,	= 6,	= 11.
73. a = 9,	= 1,	= 7,	= 12.
74. a = 8,	= 2,	= 4,	= 10.
75. a = 7,	= 3,	= 4,	= 12.
76. a = 6,	= 5,	= 4,	= 8.
77. a = 5,	= 2,	= 2,	= 7.
78. a = 4,	= 3,	= 1,	= 9.
79. a = 3,	= 2,	= 3,	= 8.
80. a = 2,	= 1,	= 1,	= 4.

Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО

7

заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.

Методические указания к решению задач

Примеры решения и оформления заданий приведены в учебно-методических пособиях [8] , [9].

Элементы линейной алгебры, аналитической геометрии и линейного программирования.

По теме «Аналитическая геометрия» рассмотрим решение типовой задачи. Задача 1.Даны вершины треугольника АВС: А(-4;8), В(5;-4), С(10;6). Найти:

1)длину стороны АВ;

2)уравнения сторон АВ и АС и их угловые коэффициенты;

3)угол А в радианах;

4)уравнение высоты СD и ее длину;

5)уравнение окружности, для которой высота СD есть диаметр;

6)систему линейных неравенств, определяющих треугольник АВС.

Решение.

1. Найдем длину стороны АВ.

Расстояние d между точками М1(х1; у1) и М2(х2; у2) определяется по формуле:

d= х		х	2 у	2	у	2	(1)
2		1			1

Подставив в эту формулу координаты точек А и В, имеем:

АВ= 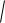5 ( 4) 2 4 8 2 81 144 15 .

2. Уравнение прямой, проходящей через точки М1(х1; у1) и М2(х2; у2), имеет вид:

	х х1			у у1			(2)
	х	х		у	2	у
	2	1				1

Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:

	х ( 4)		у 8	;	х 4		у 8	;	х 4		у 8	;
	5 ( 4)		4 8		9		12		3		4

3у–24 =–4х –16, 4х+3у–8=0 (АВ)

8

	Для нахождения углового коэффициента кАВ				прямой АВ, разрешим
	полученное уравнение относительно у:	у =	4	х		8	.
			3		3

Отсюда кАВ = 43 .

Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС:

х ( 4)		у	8	.	х 4		у 8	,	х 4		у 8	,
10 ( 4)							2				1
		6	8		14				7

х+7у–52=0 (АС).

Отсюда кАС = 17 .

3. Угол между двумя прямыми, угловые коэффициенты которых равны к1 и к2, определяется по формуле:

tg	к2 к1		(3)
	1 к к	2
	1

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив

в нее к1	= кАВ =	4	, к1	= кАС =						1			.
		3
									7
					1		(		4		)				4						1				25
		tgА		7					3							3			7						21		1,
				1 (			1	) (				4		)	1					4					25
							7		3										21						21
				А arctg1 450															0,79 рад.

4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

кСD =	1		1				3	.
				4
	кАВ						4
				3

Уравнение прямой, проходящей через данную точку М1(х1; у1) в заданном направлении, имеет вид:

			у у1 к(х х1).			(4)
	Подставив в (4) координаты точки С(10;6) и кСD =				3	, получим уравнение
					4
	высоты СD:
	у – 6 =	3	(х – 10), 4у – 24 = 3х – 30,	3х – 4у – 6 = 0 (СD).
		4
	(5)

9

Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (CD):

4х 3у 8 0

, откуда х = 2, у = 0, то есть D (2; 0)

3х 4 у 6 0

Подставив в формулу (1) координаты точек С и D, находим:

СD = 10 2 2 6 0 2 64 36 10 .

5. Уравнение окружности радиуса R с центром в точка Е( а;в ) имеет вид:

(х а)2 ( у в)2 R2

(6)

Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка СD. Воспользуемся формулами деления отрезка пополам, получим:

х			хс хD		10 2	6,	у			ус уD		6 0	3.
	Е							Е
		2		2					2		2

Следовательно, Е(6; 3) и R= СD = 5. Используя формулу (6), получаем

2

уравнение искомой окружности:

(х 6)2 ( у 3)2 25

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В.

Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:

4 10 3 6 8 50 > 0
Поэтому искомое неравенство имеет вид:	4х+3у 8 0 .

Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:

	х 5		у	( 4)	,	х 5		у 4	,	х 5		у 4	,
	10 5		6	( 4)		5		10		1		2

2х у 14 0 (ВС).

Подставив в последнее уравнение координаты точки А, имеем:

2( 4) 8 14 30 < 0. Искомое неравенство будет 2х – у – 14 0 . Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: 5 7( 4) 52 75 < 0. Третье искомое

неравенство будет х+7у –52 0 . Итак, множество точек треугольника АВС определяется системой неравенств:

10