
- •Тема 2. Элементы аналитической геометрии на плоскости.
- •Основные формулы аналитической геометрии.
- •Примеры решения задач.
- •Вопросы для самопроверки.
- •Тема 3. Основы векторной алгебры.
- •3.1 Операции над векторами.
- •Векторное произведение
- •Смешанное произведение.
- •3. 2 Примеры решения задач.
- •3. 3 Вопросы для самопроверки.
- •Тема 4. Введение в анализ.
- •Понятие предела.
- •4.2 Способы раскрытия неопределённостей вида и .
- •Первый и второй замечательные пределы.
- •Непрерывность функции. Точки разрыва.
- •Вопросы для самопроверки.
- •Тема 5. Производная и дифференциал функции одного аргумента.
- •5. 1 Определение производной, дифференциала.
- •Основные правила дифференцирования.
- •Примеры решения задач.
- •Вопросы для самопроверки.
- •Тема 6. Приложения производной к исследованию поведения функции и построению графика и к другим задачам.
- •План исследования функции и построения графика.
- •Использование производной в задачах прикладного характера.
- •План действий при решении задач прикладного характера.
- •Нахождение наибольшего и наименьшего значения функции на отрезке.
- •Вопросы для самопроверки.
Тема 4. Введение в анализ.
Пискунов, гл 1, § 1-9, упр 1-9, 39, 40
Гл 2, § 1-5, упр 1-6, 9-29, § 6-8,
Упр 31-35, 41-48, § 9, 10, упр 57-59
§ 11, упр 60-62.
Понятие предела.
Определение.Числоаназывается пределом функцииy=f(x)
в т.![]() если для любого сколько угодно малого
наперёд заданного ε
>0 найдётся такое δ>0 (δ=δ(ε)), что
выполняется неравенство
если для любого сколько угодно малого
наперёд заданного ε
>0 найдётся такое δ>0 (δ=δ(ε)), что
выполняется неравенство ![]() <
при
<
при ![]() <
<
![]()
Этот факт записывается
так:
![]()
Если ![]() ,
то говорят, что функция имеет пределом
число a
на бесконечности (x→∞).
,
то говорят, что функция имеет пределом
число a
на бесконечности (x→∞).
Если ![]() ,
то функцию
,
то функцию ![]() называют бесконечно большой величиной
в окрестности т.
называют бесконечно большой величиной
в окрестности т.![]() .
.
Если ![]() ,
то f(x)-
бесконечно большая величина на
бесконечности (x→∞).
,
то f(x)-
бесконечно большая величина на
бесконечности (x→∞).
Если ![]() ,
то
,
то ![]() -
бесконечно малая функция (величина) в
окрестности т. X0
.
-
бесконечно малая функция (величина) в
окрестности т. X0
.
Если ![]() ,
то
,
то ![]() -
бесконечно малая величина на бесконечности
(x→∞).
-
бесконечно малая величина на бесконечности
(x→∞).
При
вычислении пределов используются
теоремы о пределах, а также 1-ый
замечательный предел ![]()
второй
замечательный предел ![]()
![]() ,
а также формулы
,
а также формулы ![]() ,
,
![]()
![]()
4.2 Способы раскрытия неопределённостей вида и .
I.
Если![]() то можно использовать три способа
раскрытия этой неопределённости.
то можно использовать три способа
раскрытия этой неопределённости.
1-ый способ.Разложить и числитель и знаменатель дроби на множители, затем сократить на общий множитель.
Пример.

![]()
Ответ: где 2- предельное значение аргумента, (-1) -
предельное значение функции y.
2-ой способ.Использовать правило Лопиталя, т.е использовать равенство:

Пример: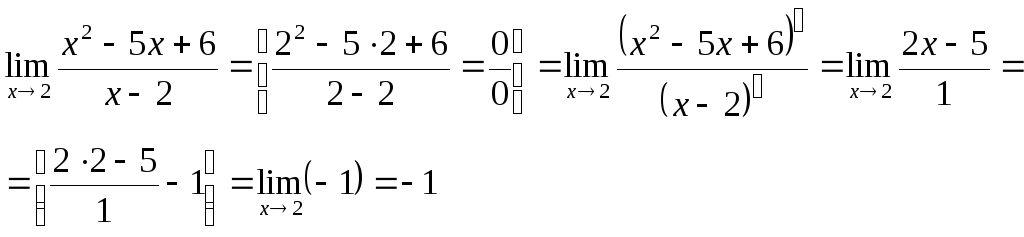
3-ий способ. Применить таблицу эквивалентности бесконечно малых.
Таблица.
1. 
2.

![]()
3.

![]()
4.

![]()
Пример:Найти![]()
Решение.
![]()
 II.
Если
II.
Если![]() то можно использовать три способа
раскрытия этой неопределённости.
то можно использовать три способа
раскрытия этой неопределённости.
1-ый способ.Использовать правило Лопиталя.
Пример.Найти![]()
Решение: 
2-ой способ. Разделить все слагаемые числителя и все слагаемые знаменателя на старшую переменную дроби.
Пример.Найти [
[![]() -бесконечно
малые величины]=
-бесконечно
малые величины]=![]()
Ответ:
![]()
Первый и второй замечательные пределы.
1.
![]() - первый замечательный предел.
- первый замечательный предел.
Замечание. При x0sinx~x
Пример 1.
Найти

![]()
![]()


если
заменить ![]() ,
т.к
,
т.к ![]() ,
,
![]() то
то

![]()
Заметим,что показатель степени обратен по величине второму слагаемому в основании.
Пример 2. представили основание в виде
суммы 1 и некоторой бесконечно малой
величины.
представили основание в виде
суммы 1 и некоторой бесконечно малой
величины.
Выполненные тождественные преобразования в показателе степени, позволяют выделить 2-ой замечательный предел. ( в квадратных скобках)
Непрерывность функции. Точки разрыва.
Определение 1.Функция![]() называется непрерывной в точке x0
, если выполняется равенство:
называется непрерывной в точке x0
, если выполняется равенство: ![]()
Определение
2. Функция ![]() называется непрерывной в точке
x0
, если
называется непрерывной в точке
x0
, если ![]()
где
![]() соответственно приращение аргумента
и приращение функции.
соответственно приращение аргумента
и приращение функции.
Пример. Дана
функция

![]()
Требуется : 1). Найти точку разрыва данной функции.
2).
Найти
![]() и
и ![]()
3). Найти скачок функции в точке разрыва.
Решение.
Данная функция
определена и непрерывна в
![]()
При x=1 функция терпит разрыв, т.к меняется аналитическое выражение функции.
y

![]()
![]()
![]()
x=1- точка разрыва первого рода.
Скачком функции
называется абсолютная величина разности
между её правым и левым предельными
значениями т.е
![]() (ед). –скачок функции.
(ед). –скачок функции.
