пособие по физике формат pdf / Глава 1. Механика

Силы, работа которых не зависит от формы траектории,

называются консервативными или потенциальными.

Консервативными являются силы тяжести и упругости. Системы, в которых действуют только консервативные силы, называют

консервативными системами.

Потенциальная энергия деформированного упругого тела, обусловленная взаимодействием между собой частей тела, равна:

				kx	2
	E				.
		П		2

(1.18)

Если изменение кинетической энергии определяется работой равнодействующей всех сил, приложенных к телу, то изменение потенциальной энергии определяется работой лишь соответствующей консервативной силы (другие действующие на тело силы в расчёт не принимаются, так как не изменяют данной потенциальной энергии).

При падении тела с высоты работа силы тяжести увеличивает его кинетическую энергию на такую же величину (если других сил нет), на какую происходит уменьшение его потенциальной энергии.

Полной механической энергией называют сумму кинетической и потенциальной энергии тела.

Закон сохранения механической энергии состоит в том, что

полная механическая энергия изолированной консервативной системы при любых её переходах остаётся неизменной:

E E	K	E	П	const

(1.19)

или изменение полной энергии такой системы равно нулю:

E E	K	E	П	0.

(1.20)

В природе существуют и силы, работа которых зависит от формы кривой и длины пройденного пути (не консервативные). К ним относятся силы трения, сопротивления и т.д. Эти силы называют диссипативными. Работа диссипативных сил всегда отрицательна, так как они направлены всегда противоположно перемещению. При наличии диссипативных сил изменение полной энергии уже не будет равно нулю, а будет равно работе диссипативных сил:

E E	K	E	П	А .
				Дис

(1.21)

Поскольку работа диссипативных сил отрицательна, полная механическая энергия при их наличии не постоянна, а уменьшается.

Любые механизмы (рычаг, блок, клин, винт, наклонная плоскость) обеспечивают выигрыш в силе, но не в работе (золотое правило механики). Из-за наличия диссипативных сил полезная работа АПол всегда меньше затраченной А. Коэффициент полезного

30

действия (КПД) показывает, какую часть составляет полезная:

	А	1		АДис	1.
	Пол
	А			А

Вопросы для самоконтроля

совершённой работы

(1.22)

1.Сформулируйте закон сохранения механической энергии. Для каких систем этот закон выполняется?

2.Как связаны с работой векторы силы и перемещения?

3.Как определить работу силы, если зависимость силы от координаты перемещения тела задана графически?

4.Может ли кинетическая энергия иметь отрицательное значение?

5.Может ли потенциальная энергия иметь отрицательное значение?

6.Может ли работа диссипативных сил иметь положительное значение?

7.Приведите примеры консервативных и диссипативных сил.

§1.13. Поступательное и вращательное движение твёрдых тел. Кинематика вращательного движения

Представлять тело как материальную точку не всегда возможно. Во многих случаях любое тело можно рассматривать как систему материальных точек. Удобной моделью такой системы является понятие абсолютно твердого тела.

Абсолютно твердым телом называется система материальных точек, где расстояние между любыми двумя из них неизменно (в этом случае будет неизменной и форма тела). Этой моделью удобно пользоваться в тех случаях, когда можно пренебречь деформациями тел.

Для таких тел возможны два вида движения – поступательное и вращательное.

Поступательным называют такое движение, при котором каждая линия, соединяющая две любые точки тела, сохраняет неизменным направление в пространстве. В этом случае все точки твердого тела двигаются по одинаковым траекториям, поэтому для

31

описания поступательного движения достаточно описать движение одной точки.

Вращательным называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями с центрами, лежащими на одной прямой, называемой осью вращения. Ось вращения может лежать вне тела или проходить через него. Траектории всех точек лежат в плоскостях, перпендикулярных оси вращения.

Для характеристики вращательного движения вводят угловые величины. Угловым перемещением называется угол, на который поворачивается перпендикуляр, опущенный из любой точки А тела на ось вращения (рис. 1.12)

Ось

r

Рис. 1.12

S

А

Угол

измеряется в радианной мере как отношение длины

дуги

S

окружности, стягиваемой этим углом, к радиусу этой

окружности, определяющей траекторию точки А.

Угол поворота

за

	S	.	(1.23)
	r

некоторый промежуток времени

t

один и тот же для любой точки твёрдого тела, и в этом заключается преимущество угловых координат.

Угловой скоростью называется первая производная от

углового перемещения по времени:			d		.
			dt
Из последнего выражение и (1.23) получим связь
угловой скорости с линейной: V	dS			d (r )		r	d	. Таким
	dt						dt
					dt
образом,
V r.								(1.24)

Тогда нормальное (центростремительное) ускорение из (1.4) при подстановке (1.24) будет равно:

32

V 2

an r 2 r. (1.25)

Тангенциальное ускорение:

	a		dV		d ( r)	r	d	r ,	(1.26)
			dt		dt		dt
где	угловое ускорение,				которое есть первая				производная по

времени от угловой скорости и вторая производная от углового перемещения:

	d		d
			2
	dt		dt	2	.

(1.27)

Поскольку линейная скорость – векторная величина, то имеет смысл и угловую скорость считать вектором, направление которого можно как-то связать с направлением вращения. Эту связь

устанавливают с помощью правила буравчика (правого винта).
Вектор		направлен вдоль оси вращения в сторону поступательного

движения правого винта при кручении его в направлении вращения
точки А вокруг этой оси. При этом определении всегда V.
Вектор углового ускорения		также направлен	вдоль оси

вращения. Поскольку ось вращения принимается неподвижной, то
вектор угловой скорости
	изменяется только по величине. При
		вектор углового ускорения	имеет то
увеличении модуля вектора

же направление, что и
	, а при уменьшении – противоположное. В

математике такие векторы называют псевдовекторами или аксиальными (осевыми) векторами.

Формулы (1.24), (1.25), (1.26), связывающие линейные и

угловые величины, теперь можно записать и в векторной форме:
	V [ , r ], an [ ,V ],				a	[	, r ].		(1.28)
Здесь	каждый		вектор	определяется			через		векторное
произведение	двух	других. Так		как					точки А
					радиус-вектор r

перпендикулярен оси вращения, вдоль которой направлены векторы
	и , то сомножители во всех этих векторных произведениях

взаимно перпендикулярны.

Наряду с угловой скоростью часто используется частота вращения n число полных оборотов, сделанных в единицу времени, и период вращения T , равный времени одного полного оборота:

33

n

то

	1	. Поскольку полный оборот соответствует углу в						2	радиан,
	T
		n		,	T	2	.		(1.29)
			2

Вопросы для самоконтроля

1.Что такое абсолютно твёрдое тело?

2.Какие виды движения твёрдого тела вы знаете? В чём их суть?

3.Назовите основные угловые характеристики вращательного движения и единицы их измерения.

4.Напишите основные соотношения между линейными и угловыми величинами вращательного движения.

5.Во сколько раз надо увеличить угловую скорость вращения Земли, чтобы все тела на её поверхности стали невесомыми?

§1.14. Основное уравнение динамики вращательного движения

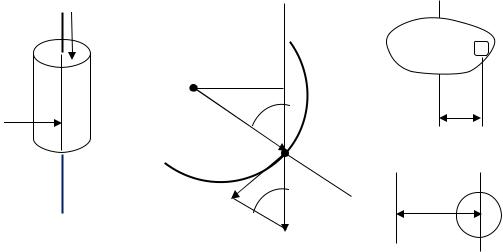
Рассмотрим твердое тело, например, диск с неподвижно закреплённой осью (рис. 1.13). Для того чтобы этот диск получил угловое ускорение, необходимо приложить к нему силу. Очевидно, если эта сила будет направлена вдоль оси вращения, то никакого

углового ускорения диск не		получит (на рис. 1.13 сила с таким
направлением обозначена как	F ).

Только сила, имеющая перпендикулярную составляющую относительно оси вращения, может сообщить диску угловое ускорение. Однако, если сила, перпендикулярная оси вращения,

приложена к точке, лежащей на оси вращения (на рис. 1.13 такая сила
обозначена как	F ), то эту силу силы реакции на опорах оси

полностью скомпенсируют и углового ускорения диск не получит. Угловое ускорение в данном случае будет вызываться лишь силой, имеющей перпендикулярную к оси вращения составляющую при условии, что линия действия этой силы не будет пересекать ось вращения.

Рассмотрим простой пример. Пусть материальная точка А массой m движется на малом участке окружности (предположим – на

34

невесомой нити) под действием силы					F	,	лежащей в плоскости этой
окружности		(рис.1.14).	По	второму				закону	Ньютона:
ma	F F sin .

.

.

F 

F

Zc

Рис.1.13

О

		l
	r
		А
	F	F

Рис. 1.14

Z

r

а) ri

Z

a

б)

Рис. 15

Умножим правую и левую части							на	r	и	выразим
тангенциальное ускорение через угловое согласно (1.26). Получим:
		mr		2	rF sin .					(1.30)
Величина, стоящая в правой части данного выражения,
называется моментом силы:						M rF sin lF ,		где l r sin
плечо силы F ,	то есть кратчайшее расстояние от линии действия
силы F до оси вращения.
Величина	mr	2	J			называется	моментом			инерции

материальной точки относительно оси. Тогда в новых величинах соотношение (1.30) примет вид:

M J или М / J ,

т.е. угловое ускорение прямо пропорционально моменту силы и обратно пропорционально моменту инерции.

Из последних соотношений следует справедливость векторного

соотношения:
	M J ,		(1.31)

где вектор момента силы определяется из векторного произведения:
	M [r , F ].			(1.32)
Соотношение (1.31)	называется			основным уравнением
динамики вращательного	движения. Оно аналогично второму
		35

закону Ньютона. Роль массы здесь играет момент инерции	mr	2	J ,

роль силы – момент силы M [r , F ], а вместо линейного ускорения
стоит угловое – .
Пусть некоторое твёрдое тело вращается около неподвижной
оси Z. Мысленно	разобьём	его на малые		элементы массой	m ,
					i
расположенные на	разных	расстояниях r		до оси вращения.	Для
			i

каждого из элементов, составляющих тело, можно воспользоваться

выражением

mr

2 J

i

Mi

, а затем

просуммировать по

всему

i

i

телу: Ji i Mi .

i

i

Угловое

ускорение

одинаково

для всех частей

тела

i

const,

поэтому его можно вынести за знак суммы. Для

заданной оси вращения

z сумма

J

i

m r 2

J

z

(1.33)

i i

i

i

есть величина постоянная, её называют моментом инерции тела относительно данной оси вращения.

При суммировании моментов сил, действующих на малые элементы тела нужно учесть, что согласно третьему закону Ньютона внутренние силы попарно равны и противоположно направлены, поэтому результирующий момент внутренних сил, приложенных ко

всем элементам тела, равен нулю, и, следовательно,
J z M z ,	(1.34)

где M z результирующий момент внешних сил, приложенных к телу

в целом.

Момент инерции тел симметричной формы может быть выражен простыми соотношениями:

для обода J mR2 ,

для сплошного диска J 12 mR2 ,

для шара	J	2	mR	2	,
		5
			R
где m масса тела, а				его радиус.

36

Если известен момент инерции тела

Jc

относительно оси,

проходящей через центр масс

С(x	, y	, z	c	),
c	c

то момент инерции

относительно любой другой оси, параллельной данной и отстоящей от

неё на		расстоянии			a,	может быть найден по теореме Штейнера:
J J		ma	2	.
	c

Вопросы для самоконтроля

1.Что такое момент силы?

2.Что такое момент инерции материальной точки?

3.Напишите основное уравнение динамики вращательного движения. Укажите его аналогию со вторым законом Ньютона.

4.Что такое момент инерции тела относительно оси вращения? Как он связан с результирующим моментом внешних сил, приложенных к телу в целом?

5.Обод и сплошной шар одинаковой массы и радиуса вращаются равноускорено вокруг своих осей вращения, проходящих через их центры масс, перпендикулярных их плоскости вращения, с одинаковым ускорением. Как будут соотноситься между собой их результирующие моменты действующих внешних на эти тела сил, вызывающих эти вращения?

§1.15. Момент импульса тела

Моментом импульса тела относительно оси вращения

z	называют произведение момента инерции тела				J	z	относительно
данной оси на угловую скорость :
			Lz	J z .			(1.35)
		Здесь вектор момента импульса		Lz имеет то же направление,
что и
		по оси вращения. Данное уравнение динамики вращения

имеет аналогию с уравнением импульса поступательного движения, где в качестве импульса фигурирует момент импульса, в качестве массы – момент инерции, а в качестве скорости – угловая скорость. Аналогично поскольку по второму закону Ньютона производная от импульса по времени равна силе, то следует ожидать, что производная от момента импульса по времени будет равна моменту силы

37

Это уравнение

полагая	J	z	const,

	dL	z
			M .	(1.36)
	dt

эквивалентно уравнению (1.34). В самом деле,
	dL	z		d (J )				d
имеем:				z		J	z		J	z	.
	dt			dt				dt

Для материальной точки момент импульса может быть выражен

иначе. Для неё J		mr	2	, а линейная скорость	r ,	откуда
	z
L mr r r m rP,				или в векторной форме:

						P],		(1.37)
			L [r
где			радиус-вектор материальной точки, а				P её импульс.
	r
	Из (1.36) следует, что если результирующий момент внешних
сил	M	равен нулю, то момент импульса тела остаётся постоянным:
								(1.38)
			L J	z	const.
			z

Данное выражение описывает закон сохранения момента импульса для вращающегося тела.

Из этого закона следует, что при изменении момента инерции

J z

будет меняться и угловая скорость. Такое изменение происходит

при перемещении частиц тела. В частности, при выполнении элемента вращения в фигурном катании фигурист прижимает раздвинутые руки к телу, уменьшая момент инерции и увеличивая на соответствующую величину угловую скорость вращения.

Вопросы для самоконтроля

1.Что такое момент импульса тела относительно оси вращения? Как определить его направление?

2.Сформулируйте закон сохранения момента импульса.

3.Что произойдёт с угловой скоростью вращения планеты Земля, если по каким-то причинам начнёт сжиматься её объём?

§1.16. Кинетическая энергия вращающегося тела

Для нахождения кинетической энергии тела, вращающегося вокруг неподвижной оси, разобьём его на малые частицы и найдём сумму энергий всех частиц тела:

38

m

2

1

2 2

E

E

i

i

m r

.

K

Ki

2

2

i i

i

i

i

Но величина

	i i	2	J
	m r
i

есть момент инерции тела, поэтому

окончательно кинетическая энергия вращения тела будет иметь вид

				J	2
	E				.
		K		2

(1.39)

Это выражение аналогично выражению для кинетической энергии поступательного движения, где в качестве массы фигурирует момент инерции, а в качестве скорости поступательного движения – угловая скорость.

Работа, совершаемая над телом, вращающимся вокруг

неподвижной оси, при повороте			на		угол				2		будет равна
										1
изменению его кинетической энергии вращения:
	J	2		J		2
		2
A	2			1	1		.
	2				2

Если тело участвует одновременно во вращательном и поступательном движениях, то его полная кинетическая энергия будет равна сумме кинетических энергий соответствующих движений:

						mV	2		J	2
			E							,
				K		2			2
	где	mV 2	кинетическая энергия поступательного движения (1.16).
		2

Вопросы для самоконтроля

1.Напишите выражение для кинетической энергии вращательного движения. Укажите его аналогию с соответствующим выражением поступательного движения.

2.Сплошной цилиндр массой 10 кг катится без скольжения по горизонтальной плоскости с постоянной скоростью 1 м/с. Чему равна его полная кинетическая энергия?

3.Сплошной и полый цилиндры одинаковой массы и радиуса вкатываются без скольжения вверх по наклонной плоскости с одинаковой начальной угловой скоростью. Какой из цилиндров поднимется выше?

39