пособие по физике формат pdf / Глава 1. Механика

§1.17. Гармонические колебания

Колебаниями называют движения, повторяющиеся во времени. Если значения числовых характеристик этого движения повторяются через равные промежутки времени, колебания называются периодическими. Если изменения этих характеристик происходят по закону синуса или косинуса, то колебания называются гармоническими. Например, гармоническое колебание может быть задано уравнением:

x

x Asin( t 0 ),

A

(1.40)

где

смещение

от положения равновесия,

амплитуда

колебания (максимальное смещение),

( t

0

)

фаза колебания,

t

время,

циклическая частота, 0

начальная фаза.

Колебания характеризуют также

периодом

T

временем

одного полного колебания и частотой

числом

колебаний в

единицу времени:

1

.

T

Эти характеристики связаны с циклической частотой (угловой

скоростью) соотношениями:

2

2

.

(1.40а)

T

Геометрическая

интерпретация

гармонического

колебания

может быть представлена в виде графика в координатах

x, t (рис.

1.16).

x

А

t

Ā

Т

φ

О

х

Рис. 1.16

Рис. 1.17

Для получения таких графиков на практике используют принцип временной развёртки – колебательное движение накладывают на поступательное прямолинейное движение с постоянной скоростью (движущаяся бумажная лента, луч осциллографа).

40

Наряду с графическим можно пользоваться и векторным представлением гармонических колебаний (рис. 1.17). Проекция

вектора A

на ось x равна x Acos , где угол между вектором

и осью. Если вектор равномерно вращается с угловой скоростью , то кинетическое уравнение для углового перемещения будет иметь

вид t	0	, при этом проекция вектора
гармоническому закону: x Acos( t			0	).

A

будет изменяться по

Таким образом, гармоническое колебание геометрически изображается в виде проекции вектора A, имеющего модуль, равный

амплитуде колебаний, и вращающегося с угловой скоростью			,
равной циклической частоте колебаний, т.е. 2	2	.
	T

Пусть колебание материальной точки происходит по синусоидальному закону (1.40). Линейная скорость точки выразится через производную от этой функции:

где

dx dt

	A
m

A cos( t		)	sin( t				),	(1.41)
	0			0
		m				2
амплитуда скорости. Из сравнения						(1.39)		и (1.41)

следует, что скорость опережает по фазе смещение на четверть периода. Ускорение точки найдётся как производная от скорости

a

d

d

A cos( t

) A 2 sin( t

) a

sin( t

),

0

0

0

dt

dt

m

где а

m

A 2

амплитуда ускорения.

Из

уравнений

гармонических колебаний для ускорения

a

и смещения

x (1.39)

следует, что

a

2

x.

(1.42)

Следовательно, при гармоническом колебании ускорение пропорционально смещению и направлено противоположно ему, т.е. всегда к положению равновесия, как и возвращающая сила.

Вопросы для самоконтроля

1.Что называется колебательным движением?

2.Какие из колебаний называются периодическими?

3.Напишите уравнение гармонического колебания.

41

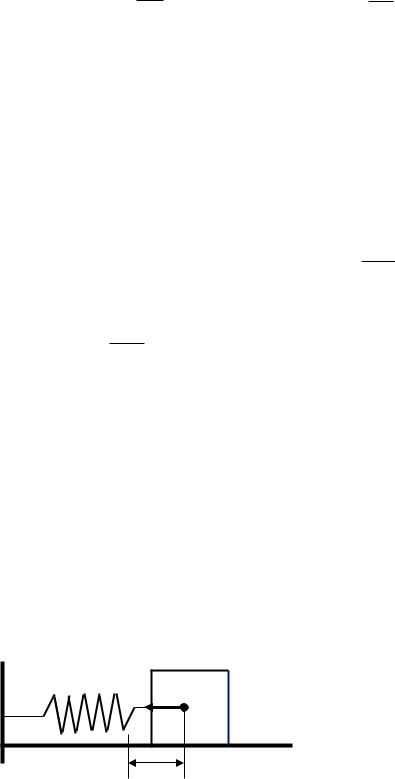
4. В некоторый момент времени при гармоническом колебании

	смещение было	х	4		см,	а ускорение
				2

равна частота и период колебаний?

а16 см .

с2

Чему

§1.18. Пружинный, математический и физический маятники

Рассмотрим примеры систем, совершающих гармонические колебания в отсутствии сил трения и сопротивления. Такие системы называют гармоническими осцилляторами. Поскольку ускорение

есть вторая производная по времени от смещения, т.е.

(1.42) имеем:

d	2		x		2
						x 0.
dt		2

		d	2		x
	a					,
		dt		2

то из

(1.43)

Пружинный маятник представляет собой колебательную систему, состоящую из груза массой m, присоединённого к пружине

жёсткостью k. Массой пружины в сравнении с массой груза можно пренебречь. Установим пружину горизонтально (рис. 1.18). Будем считать, что груз движется по горизонтальной поверхности без трения. Если груз сдвинуть от положения равновесия, то на него будет действовать сила упругости пружины, направленная к положению равновесия. Поэтому её называют возвращающей силой. При малых отклонениях от положения равновесия эта сила подчиняется закону Гука: F kx.

Если груз отклонить от положения равновесия, то он начнёт совершать колебания (рис. 1.18).

 

F

m

О

х

Рис. 1.18. Пружинный маятник

42

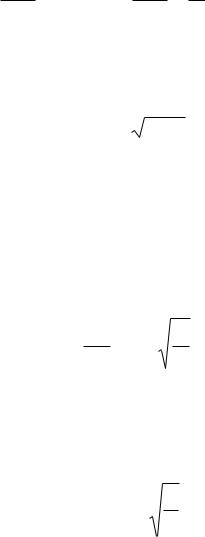
Уравнение движения груза, согласно второму закону Ньютона, будет иметь вид

d

2

x

d

2

x

k

m

kx или

x 0.

dt

2

dt

2

m

Это дифференциальное уравнение движения маятника. Из сравнения уравнений (1.43) и (1.44) пружинный маятник совершает гармонические циклической частотой

(1.44)

пружинного следует, что колебания с

k / m.

(1.45)

Эту частоту называют частотой собственных колебаний маятника или собственной частотой. Собственная частота определяется параметрами самой системы (в данном случае упругостью пружины k и массой груза m ) и не зависит (в пределах применимости закона Гука) от амплитуды.

Из (1.40а) получается формула для вычисления периода колебаний пружинного маятника

	T	2	2	m	.
				k

(1.46)

Математическим маятником называют модель,

представляющую собой материальную точку, подвешенную на нерастяжимой невесомой нити. При малых углах отклонения от положения равновесия период колебаний математического маятника не зависит от его массы и амплитуды колебаний:

	T 2	l	,	(1.47)
		g

где l длина маятника, g ускорение свободного падения.

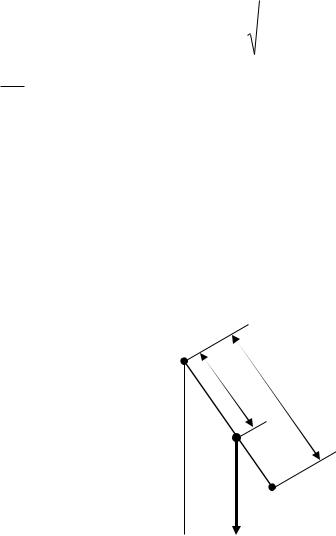
Физический маятник – это твёрдое тело, имеющее неподвижную ось вращения О, не проходящую через центр масс C (рис. 1.19). Если маятник оттолкнуть от положения равновесия, то возникает вращающий момент, обусловленный силой тяжести, приложенный к центру масс C, и возвращающий маятник к положению равновесия.

Применяя основное уравнение динамики вращательного движения, можно получить уравнение движения, подобное (1.43) и найти период колебаний физического маятника:

43

				T 2		L		,		(1.48)
						g
	где L	J		приведённая длина физического маятника,						J момент
		ml
						О, l
	инерции	маятника относительно оси							расстояние от оси

вращения до центра масс, m масса маятника.

Приведённая длина физического маятника равна длине математического маятника, имеющего такую же собственную частоту. Точка О1 (рис. 1.19) называется центром качания. Центр качания О1 и точка подвеса О обладают свойством взаимозаменяемости в том смысле, что если ось вращения будет проходить через точку О1, то точка О будет центром качания, при этом частота колебаний будет

прежней.
О
l	L

С

О1

mg

Рис. 1.19

Из рассмотренных колебательных систем видно, что их движение описывается уравнениями, имеющими одинаковый вид. Это связано с тем, что в них возвращающая сила была пропорциональна смещению (как в законе Гука). Определив конкретный вид возвращающей силы, нетрудно найти собственную частоту любой колебательной системы.

Вопросы для самоконтроля

1.Что называется гармоническим осциллятором?

2.Как изменится частота колебаний пружинного маятника при уменьшении его амплитуды в четыре раза?

3.Как изменится период колебаний математического маятника при увеличении его массы в четыре раза?

44

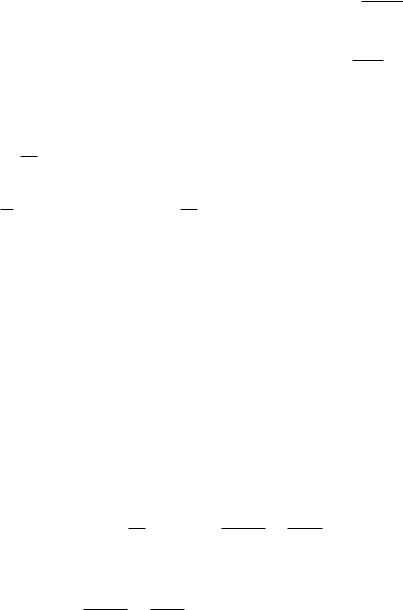
§1.19. Энергия гармонического осциллятора

Энергия гармонического осциллятора слагается из двух частей –

кинетической энергии движущейся массы

потенциальной энергии упругой части системы

			m	2
E
	K		2

kx2

EП 2 .

и

Если

система совершает гармонические колебания, то смещение и скорость определяются соотношениями (1.40) и (1.41), и эти энергии будут

EK

m

2

2

cos

2

( t 0 ),

иметь вид:

2

A

E

k

A

2

sin

2

( t

)

m

2 2

sin

2

( t

),

П

2

0

2

A

0

т.к. из (1.45)

2

k / m.

Потенциальная энергия в момент прохождения точки

положения

равновесия

( x Asin( t

0

) Asin( n) 0

при

t ( n

0

) / )

равна

нулю,

а

кинетическая

в этот

момент

максимальна.

А

в

моменты

n 0

наоборот,

EП

t

/ ,

2

максимальна,

а

E

K

0. При

колебаниях происходит

переход

потенциальной энергии в кинетическую и обратно. Так как потери в гармоническом осцилляторе отсутствуют, то полная его механическая энергия будет оставаться постоянной:

E E	П	E	K

m				m	2	2
	2	2				kA
				m		.
	A
2				2		2

Из условия равенства максимальных значений кинетической и

m 2
	m
потенциальной энергий
	2

квадратов амплитуд скорости и

	kA
	2
			следует, что отношение
	2

смещения m2 / A2 k / m 2.

Вопросы для самоконтроля

1.Как изменится частота и максимальная скорость гармонического осциллятора, если уменьшить вдвое его амплитуду?

45

2.Как изменится полная энергия гармонического осциллятора, если увеличить вдвое его амплитуду?

3.Как изменится частота и максимальная скорость гармонического осциллятора, если увеличить вдвое его массу?

§1.20. Свободные затухающие колебания

В реальных системах свободные колебания не являются гармоническими. Под действиями диссипативных сил происходят потери механической энергии, и амплитуда колебаний постепенно уменьшается. Такие колебания называют затухающими.

Пусть теперь имеется система, в которой необходимо учесть ещё и действие силы вязкого трения. Эта сила пропорциональна скорости:

F

dx

,

тр

dt

где

коэффициент

трения.

Уравнение

движения

системы:

d

2

x

dx

d

2

x

dx

k

m

kx

или

x 0.

dt

2

dt

dt

2

m dt

m

Это линейное однородное дифференциальное второго порядка. Его общим решением будет функция

для такой

(1.49)

уравнение

x A e t cos( t	0	),
0

(1.50)

	где A0 амплитуда в			начальный		момент		времени,
										2m
	коэффициент затухания,				2	2		частота	затухающих
	колебаний (
		k / m	частота без затухания).
	Со временем амплитуда колебания уменьшается по закону:

AA0e t ,

ауменьшение частоты 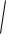2 2 будет не столь быстрым.

46

Время

уменьшится

релаксации.

в

		1		2m	,	за которое
		e 2,719281928...					раз

амплитуда колебаний называется временем

Вопросы для самоконтроля

1. Как изменяется амплитуда затухающего колебания со временем?

2.Как изменится коэффициент затухания, если увеличить вдвое массу колебательной системы?

3. Чтобы убедиться в том, что функция

x(t)

из (1.50)

действительно является решением дифференциального уравнения (1.49), подставьте её в это уравнение и получите тождество.

4.Как изменится время релаксации затухающих колебаний при увеличении массы колебательной системы в два раза?

§1.21. Вынужденные колебания. Резонанс. Автоколебания

Колебания, которые совершает система под действием внешней

вынуждающей силы:

F F	sin t,
m	в

называются вынужденными.

Уравнение движения такой колебательной системы будет иметь вид:

	d	2		x		dx
m							kx F	sin	t,
	dt		2			dt	m	в

а решением этого дифференциального уравнения будет:

	x Asin( t						0	).
					в
Здесь частота вынужденных колебаний равна частоте
вынуждающей силы		в	,	а амплитуда колебаний зависит от
амплитуды вынуждающей силы Fm						и	от соотношения частоты
вынуждающей силы в		и собственной частоты									колебательной
системы:
	A				Fm					.
				m 2 в		2 4 2 в2

Когда соотношение этих частот даёт минимальное значение знаменателя данной дроби, то наблюдается резонанс – резкое увеличение амплитуды A. Особенно сильно резонанс выражен при

47

малом коэффициенте затухания системы (

0

). Явление резонанса

может быть полезным и вредным. Его используют для настройки музыкальных инструментов, и оно же может приводить к разрушению механических систем.

Автоколебания – это колебания, поддерживаемые в системе за счёт внутренних источников энергии. Примером автоколебаний является анкерный часовой механизм, с помощью которого маятник часов получает энергию от сжатой пружины, компенсирующую её убыль из-за трения в оси и сопротивления воздуха.

Вопросы для самоконтроля

1.Как изменится амплитуда вынужденных колебаний при увеличении амплитуды вынуждающей силы в два раза?

2.Что такое явление резонанса при вынужденных колебаниях?

3.Составьте дифференциальное уравнение вынужденных колебаний без затухания.

§1.22. Механические волны в упругих средах

Волной называется процесс распространения колебаний в среде. В механических волнах колебания, возникающие в какой-либо точке упругой среды, передаются соседним точкам (частицам среды). Частицы лишь смещаются относительно положения равновесия, обмениваются энергией, но сами вместе с волной не переносятся. Процесс распространения волны – это процесс вовлечения в колебательное движение всё новых и новых частиц.

Фронт волны – это поверхность, разделяющая невозмущенную зону среды от её области, вовлечённой в колебательный процесс. Скорость волны – это скорость движения фронта волны. Скорость волны зависит от плотности упругой среды.

Частицы относительно положения равновесия могут смещаться как вдоль направления движения волны (рис. 1.20б, такие волны называют продольными), так и поперёк (рис. 1.20а, поперечные волны). В жидкостях и газах распространяются только продольные волны, а в твёрдых телах как продольные, так и поперечные.

Скорость распространения поперечной волны в струне зависит
от силы F натяжения струны и от её линейной плотности					(массы
на единицу длины) следующим образом:
u
		F .			(1.51)
	48

Величина смещения частиц

относительно равновесия в

поперечной волне (рис. 1.20а) в произвольной точке произвольный момент времени t определится соотношением(x,t) Asin (t x / u),

x

и в

(1.52)

называемым уравнением волны. Это уравнение позволяет определить смещение любой точки с координатой x в момент времени t.

Направление
распространения
волны	а)
Направление	x
колебаний
Направление
распространения
волны	б)
	x
Направление колебаний

Рис. 1.20. Поперечные а) и продольные б) волны

Если сделать относительно оси

мгновенную

равновесия

x,

фотографию всех

то функция

смещений

(x)

будет

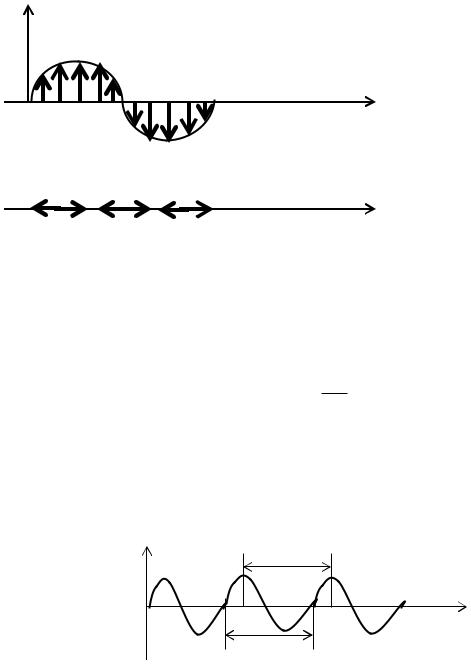
	периодической (рис. 1.21) с периодом T	2	в соответствии с (1.52).

Величина uT называется длиной волны. Длина волны определяет

расстояние между ближайшими друг к другу точками, имеющими одинаковое смещение (колеблющимися в одинаковых фазах, рис. 1.21). Иначе говоря, это расстояние, на которое волна распространится за период T.

x

Рис. 1.21

49