Барменков Методика решения задач повышенной сложности по теории 2010

2

ln 2 x

dx

ln 2 a

2

i ln a 2 i

ln x

dx

0

x2

a 2

a

4

0

x2

a 2

2

dx

.

0

x2

a2

По формуле (3.5)

ln x

ln ai

ln a

i

ln a

dx

Re i

Re

2

.

0

x2

a2

2ai

2a

2a

С учетом того, что

dx

1

arctg

x

, окончательно

0

0 x2 a2

a

a

2a

находим

ln 2 x

dx

ln 2 a

2

i ln a

2i ln a

3

x2

a2

0

2a

4

2a

4a

2

ln 2 a

.

2a

4

2

Ответ.

ln 2 a

.

2a

4

Задача 25.

Вычислить

ln 2 x

dx .

0

x2

3x

1

Решение.

Вычислим

вспомогательный

контурный

интеграл

ln 3 z

dz , где контур

изображен на рис.54. Проводя

z2

r , R

3z

1

r ,R

уже знакомые рассуждения, получаем равенство

ln 3 z

R

ln 3 x

2

ln 3 (Rei )ei

dz

dx iR

d

z 2

3z 1

r

x2

3x 1

R2 e2i

3Rei

1

r , R

0

91

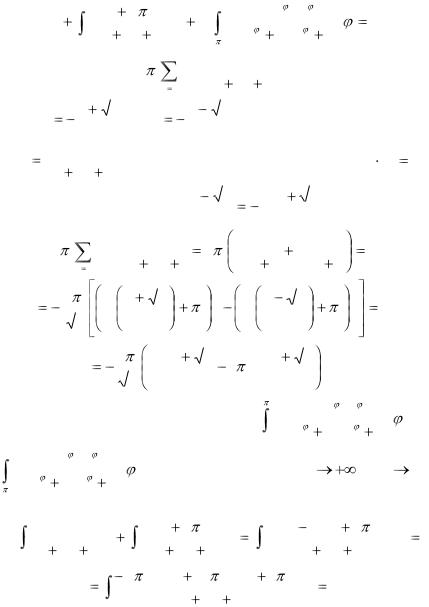
r (ln x

2

i)3

0

ln 3 (rei

)ei

dx ir

d

R

x2

3x 1

r 2 e2i

3rei

1

2

2

ln 3 z

2 i

Res

.

(3.6)

z

2

3z

k

1

zk

1

Здесь

z

3

5

и

z

3

5

– простые полюсы функции

2

1

2

2

F (z)

1

,

причем

справедливо соотношение z1

z2

1,

z2

3z

1

используя которое найдем

ln

3

5

ln

3

5

и

2

2

2

ln 3 z

ln

3 z

ln 3

z

2

2

i

Res

2

i

1

z

2

3z 1

2z1 3 2z2

3

k 1

zk

2

i

3

3

3

5

3

5

ln

i

ln

i

2

2

5

4 i

ln 3

3

5

3 2 ln

3

5

.

2

2

5

Несложно

проверить,

что

интегралы

2

ln 3 (Rei

)ei

d

и

0

R2e2i

3Rei

1

0 ln 3 (rei

)ei

d

стремятся к нулю при

R

и

r

0

2

r 2e2i

3rei

1

соответственно. Дальнейшие преобразования дают

R

ln

3 x

r (ln x

2 i)3

R ln 3

x

(ln x

2 i)3

dx

dx

dx

x 2

x 2

x 2

r

3x 1

R

3x 1

r

3x 1

R

6 i ln 2 x 12

2 ln x 8

3i

dx

r

x 2

3x

1

92

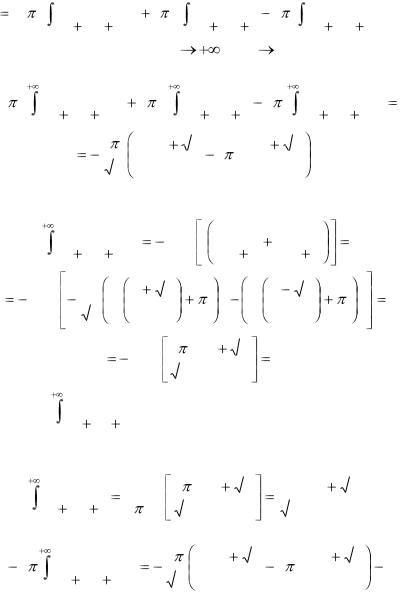
2 R

ln x

3

R

dx

R

ln 2 x

12

dx 8 i

6 i

dx.

r

x2 3x 1

r

x2

3x 1

r

x2

3x 1

Переходя к пределу при

R

и

r

0 в равенстве (3.6),

имеем

12

2

ln x

dx

8

3i

dx

6 i

ln 2 x

dx

x2

x2

x2

0

3x 1

0

3x 1

0

3x 1

4 i

ln

3 3

5

3

2

ln

3

5

.

2

2

5

Осталось отдельно вычислить два первых интеграла в левой части этого равенства. Используя формулу (3.3), получим

					ln x																1												ln	2 z										ln 2 z							2
														dx									Im i											1
			0	x2			3x 1														2											2z 3 2z															2				3
																														1
																														2																													2
	1						i											3			5																					3								5
		Im										ln																	i								ln																			i
2																			2																										2
							5
																		1	Im		4							ln		3				5								0 .
												2																		2
																								5
Интеграл							dx												можно посчитать непосредственно, но в
				0	x2			3x				1
данном случае легче воспользоваться формулой (3.4),																																																								так как сум-
ма вычетов уже найдена:
					dx							1								Re	4								ln	3				5								2							ln					3		5				.
			x2		3x 1 2																									2																										2
0																									5																					5
Подводя итог вычислениям, приходим к равенству
							2 x
6					ln								dx								4								ln	3 3				5								3					2			ln				3		5
			0 x2																															2																						2
							3x					1									5
																								93

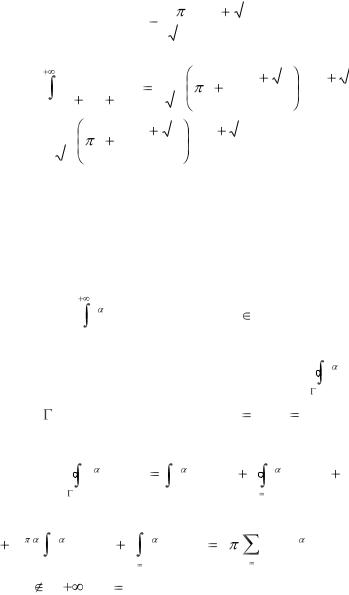
16	3		ln	3		5		,
					2
	5

откуда

				ln 2 x
							dx				2							2		ln 2		3 5				ln	3	5			.
		x2
0					3x	1				3	5											2						2
Ответ.		2		2		ln		2 3			5						ln	3		5			.
										2										2
3		5

3.3. Интегралы, содержащие дробные степени

Пусть F (z) – однозначная аналитическая функция на всей плос-

кости, за исключением особых точек, причем последние не лежат на положительной части действительной оси. В предположении,

что интеграл x F (x)dx сходится (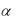 R) , требуется вычислить

0

его.

Рассмотрим следующий контурный интеграл:

z F(z)dz , где

R ,r

контур

R,r состоит из окружностей

z

r ,

z

R и разреза вдоль

отрезка [r; R]

(рис.54).

R

z F(z)dz

x F(x)dx

z F(z)dz

R ,r

r

z

R

r

n

e2 i

x F(x)dx

z

F(z)dz

2 i

Res(z

F(z)) ,

(3.7)

R

z

r

k 1

zk

где zk

[0;

) , k

1, n ,

– особые точки F (z) . Подробное обос-

нование возможности применения основной теоремы теории вычетов при выводе формулы (3.7), включающее процесс выделения

94

однозначных ветвей функции

z

и придающее смысл интегралу

z F(z)dz , смотри в монографии [4, с.268].

R ,r

Предположим, что F (x)

такова, что каждый из интегралов

z F (z)dz

и

z F (z)dz

стремится

к

нулю

при

r

0 и

z

r

z

R

R

соответственно.

Указанные

условия

выполняются, на-

пример, когда F (x)

P(x)

– рациональная функция, для которой

Q(x)

степень многочлена Q(x) ,

по крайней мере,

на две единицы боль-

ше степени многочлена P(x) .

Переходя к пределу при

r

0 и

R

в равенстве (3.7), получим

n

(1 e2 i

)

x F (x)dx

2 i

Res(z F (z)) .

0

k 1

zk

Если

не является целым, то из последнего равенства находим

2 i

n

x

F (x)dx

Res(z F (z))

1

e

2 i

zk

0

k 1

n

e

i

Res(z

F (z)) ,

Z .

(3.8)

sin

k

1

zk

Упражнение 12. В тех же предположениях относительно

F (z) ,

что и в (3.8), доказать справедливость при любом

Z формулы

n

x F (x)dx

Res( z

F (z) ln z) ,

0

k

1

zk

z

где ln z

ln

z

i arg z, 0

arg z

2 ,

а под

, как и в формуле

(3.8), понимается e

ln z .

Следующий интеграл возникает в теории роста целых функций. Он вычисляется в разных источниках (см., например, [5]).

95

Задача 26. Вычислить

x

1

dx , где

0

1.

0 1

x

Решение.

По формуле (3.8)

x

1

dx

x

dx

e

i Res

z

1

0

1

x

0

x(1

x)

sin

1

1

z

e

i e( 1) ln(

1)

e i e(

1) i

.

sin

sin

sin

Ответ.

.

sin

Задача 27. (№ 4.174 [1])

Вычислить

x

dx , где

0

x2

2x cos

1

1

1,

.

Решение.

Мы не будем рассматривать случай

0 как триви-

альный (в этом случае интеграл легко считается без применения

теории вычетов). При каждом

(

1;0) (0;1) можно применить

формулу (3.8).

В этом примере

F (z)

1

. Если

0 , то F (z)

z2

2z cos

1

имеет единственную

особую

точку

–

полюс

второго порядка

z

1, причем

Res F(z)

lim (z

)

lim (

z 1 )

1

z 1

z

1

lim

e(

1)ln z

e(

1)

i

e

i .

z 1

Тогда по формуле (3.8)

x

dx

e

i (

e i )

.

1)2

0

(x

sin

sin

Если же

0 , то функция

F (z)

имеет два простых полюса

z1

cos

isin

и z2

cos

i sin

.

При нахождении ее

96

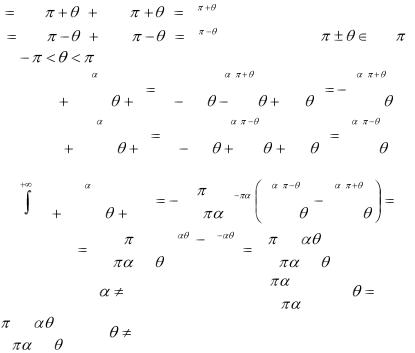
вычетов

понадобится

записать

эти точки

в

удобном

виде

z

cos(

)

i sin(

)

e(

)i ,

1

z

2

cos(

)

i sin(

)

e(

)i , замечая, что

(0;2

)

при

. С учетом этого получаем

Res

z

e (

)i

e (

)i

,

z2

2z cos

1

2(

cos

i sin

cos

)

2i sin

z1

Res

z

e (

)i

e (

)i

.

z

2 2z cos

1

2(

cos

i sin

cos

)

2i sin

z2

Следовательно, формула (3.8) дает

x

dx

e

i

e (

)i

e ( )i

0

x2

2x cos

1

sin

2i sin

2i sin

e

i

e

i

sin

.

sin

sin

2i

sin

sin

Ответ.

При

0 интеграл равен

,

если

0 ,

и

sin

sin

, если

0 .

sin

sin

97

СПИСОК ЛИТЕРАТУРЫ

1.Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного. М.: Физматлит, 2004.

2.Барменков А.Н., Бухарова Т.И., Логинов А.С., Сандракова Е.В. Методические рекомендации к решению задач по теории функций комплексного переменного.

М.: МИФИ, 2005.

3.Маркушевич А.И. Теория аналитических функций.

М. – Л.: ГИТТЛ, 1950.

4.Шведенко С.В. Начала анализа функций комплексной переменной. М.: МИФИ, 2008.

5.Гельфонд А.О. Вычеты и их приложения. М.: Ком-

Книга, 2006.

98

СОДЕРЖАНИЕ

Предисловие………………………………………………………3

1.Конформные отображения……………………………….......4

1.1.Линейная функция………………………………………...7

1.2.Дробно-линейная функция………………………………..9

1.3.Функция Жуковского…………………………………….17

1.4.Степенная функция………………………………………24

1.5.Показательная функция………………………………….31

1.6.Логарифмическая и тригонометрические функции……36

2.Вычисление контурных интегралов………………………..60

3.Вычисление несобственных интегралов…………………...77

3.1.Лемма Жордана и связанные с ней интегралы………….77

3.2.Интегралы, содержащие логарифм……………………....85

3.3.Интегралы, содержащие дробные степени……………...94

Список литературы……………………………………………....98

Анатолий Николаевич Барменков Елизавета Васильевна Сандракова Владимир Борисович Шерстюков Ольга Владимировна Шерстюкова

МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ ПО ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Учебно-методическое пособие

Редактор Т.В. Волвенкова

Подписано в печать 10.12.2009. Формат 60х84 1/16. Печ.л. 7,0. Изд.л. 7,0. Тираж 100 экз. Изд. №1/4/68. Заказ № 31

Национальный исследовательский ядерный университет «МИФИ», 115409, Москва, Каширское шоссе, 31.

ООО «Полиграфический комплекс «Курчатовский», 144000, Московская область, г. Электросталь, ул. Красная, 42