Барменков Методика решения задач повышенной сложности по теории 2010

ai

f (z)dz

2

i Res f (z)

2e 2 .

i

PR

2

С другой стороны,

R eax

R i eaz

R i eaz

R

eaz

f (z)dz

R

dx

dz

dz

i

dz

P

ch x

R

ch

z

R i ch

z

R

ch z

R

I1 (R) I 2 (R) I3 (R) I 4 (R) .

Преобразуем отдельно третье слагаемое, сделав замену переменной

z x i (тогда x

[R; R], dz

dx ):

R i

eaz

R

ea( x i)

R

eax

I

3

(R)

dz

dx

eai

dx

R i ch z

R ch (x i)

ch x

R

R eax

eai

dx eai I1 (R) .

R ch

x

Поскольку

0 eax

R

eax

R e

ax

R eax

R ch ax

I1 (R)

dx

dx

dx

dx 2

dx,

0 ch

0 ch x

R ch x

0

ch

x

x

0

ch

x

то

I (R)

I

(R)

(1

eai )I (R)

2(1

eai )R

ch ax

dx

3

1

1

0 ch

x

	ai		ai		ai R
2e 2		e 2		e 2
				0

ch ax		ai		a	R	ch ax
			cos				dx .
	dx 4e 2
ch x			2		0 ch x

Оценим теперь I2 (R) и I4 (R) . Имеем

I

2

(R)

R i eaz

dz

i 1

ea( R ix)

dx

eaR 1

dx

R ch

z

ch

(R ix)

ch

(R ix)

0

0

2eaR

1

dx

2eaR

0 при R

, так как

0

e Rei x

e Re i x

e R

e R

a

.

81

Аналогично (проверьте самостоятельно),						I4 (R) 0 при R	.
Переходя к пределу в равенстве
4				ai
I	k	(R)	2e 2			,

k1

сучетом полученной выше информации о поведении Ik (R) , при-

ходим к соотношению

		ai						ai
	4e		cos	a		ch ax	dx 2e
		2						2	, откуда следует
	2				0 ch x

Ответ.	1			.
	2cos	a
	2
					eax
Упражнение 11. Вычислить						dx , 0 a	.
					ch x

1

Ответ. . cos a2

Рассмотрим еще несколько несобственных интегралов, взятых по лучу.

x2m

Задача 21. Вычислить

dx , где m ,

n – натуральные

0

1

x2n

числа и

m

n .

Решение.

Особые точки функции

f (z)

z2m

найдѐм

из

z2n

1

уравнения

z2n

1,

решая

которое

получим

(1 2k )

i

zk e

2n

,

k

0, 2n 1. В качестве вспомогательного контура

выберем

контур

R ,

состоящий

из

отрезков

лучей

arg z

0 ,

arg z

и соединяющей их дуги окружности

z

R

(рис.53).

n

82

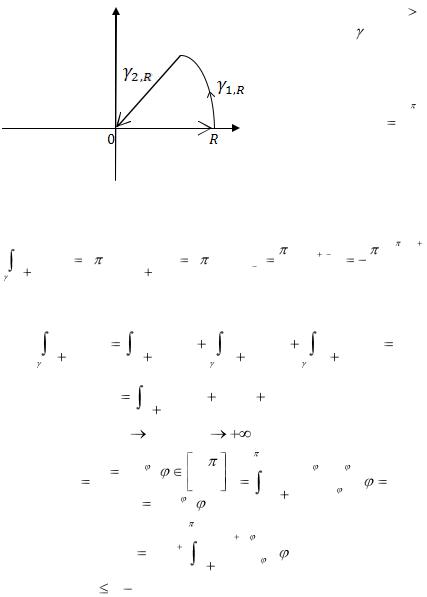
При любом				R 1
внутрь R			попада-
ет	единственная
особая точка				f (z) ,
а именно,			простой
				e		i .
полюс		z	0		2n

Поэтому

Рис.53

z

2m

z

2m

z

2m

i

i

(2m 1)

i

dz 2

i Res

2

i

0

z

2m 1 2n

e

2n

.

1 z

2n

1

z

2n

2n 1

n

0

n

z0

2nz0

R

С другой стороны,

z 2m

R

x2m

z 2m

z 2m

dz

dx

dz

dz

1 z 2n

1 x2n

1 z 2n

1 z 2n

R

0

1, R

2, R

R

x

2m

dx I1 (R) I 2 (R) .

0

1

x2n

Докажем, что I1(R)

0

при R

. Действительно,

z Rei

R 2m e2mi iRei

,

0;

n

I1 (R)

n

d

dz

iRe

i

d

0

1 R 2n e2ni

e(2m 1)i

iR2m 1

n

d .

0

1

R2ne2ni

По условию m

n

1, поэтому

83

I (R)

iR2m 1

n

e(2m 1)i

d

R2m 1 n

d

1

1 R2ne2ni

R2ne2ni

1

0

0

R2m 1

R2n 1

R2m 1

n

d

0 при

R

.

0

R2n 1 n R2n

1 n R2n 1

i

2

m

i

i

R

x 2m e

z

xe n , x [R;0]

n

Далее,

I

2

(R)

e n

dx

i

1 x 2n e2

i

dz e n dx

0

(2m 1)

i R

x2m

1

e

n

x2n dx .

0

Таким образом, устремляя в равенстве

z2m

R

x2m

dz

dx I1 (R) I2 (R)

1 z2n

1 x2n

R

0

переменную R к

, получаем

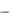ni e

откуда

(2m 1)	i		(2m 1)	i			x2m
		1 e			1
2n			n				x2n dx ,
			0

(2m 1)

i

2m

x

i

e

2n

i

1

dx

0 1 x

2n

n

(2m 1)

i

n

(2m 1)

i

(2m 1)

i

e

n

1

e

2n

e

2n

2n sin (2m 1) .

2n

Ответ.				.
	2n sin	(2m 1)
		2n

84

3.2. Интегралы, содержащие логарифм

Интерес представляет				несобственный интеграл по полуоси
(0; )	в случае, когда z			0 является точкой ветвления соответ-
ствующей вспомогательной функции комплексной переменной.
Пусть	F (z)	P(z)	–	рациональная функция, не имеющая по-
		Q(z)

люсов на неотрицательной части действительной полуоси, причем степень Q(z) , по крайней мере, на 2 единицы больше степени

многочлена P(z) , и все коэффициенты многочленов P и Q веще-

ственны. Вычислим

F (x) ln xdx

0

(рекомендуем проверить сходимость этого интеграла при указанных предположениях относительно F (x) ).

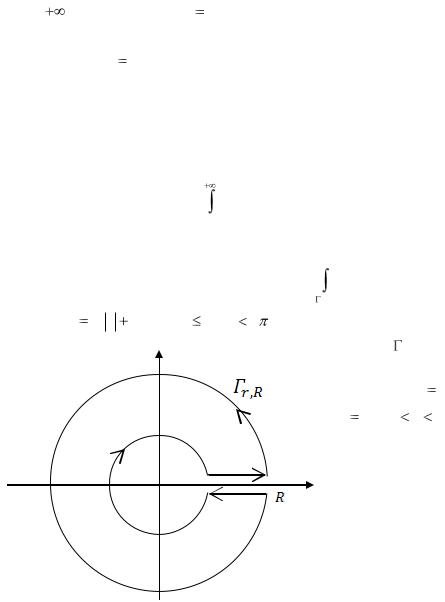
Для этого рассмотрим контурный интеграл F (z)(ln z)2 dz ,

r ,R

где ln z ln z i arg z , 0 arg z 2 , – главное значение Ln z , а

		контур					r , R			со-
		стоит из окружно-
Рис.54		стей						z		r ,
			z		R ,	0		r		R ,
		и разреза						вдоль
		отрезка						[r; R]
		(рис.54). Выбирая
		достаточно боль-
	r
		шое			R	и доста-
		точно				малое				r ,
		можно					считать,
		что			все		полюсы
		85

F (z) лежат внутри контура	r , R .
Тогда
	k
F (z)(ln z)2 dz	2 i		Res{F (z)(ln z)2 },
	j	1	z j
r , R

где z j – все полюсы F (z) .

С другой стороны, производя стандартную замену переменных в интегралах по окружностям, можно записать

	R		2
F(z)(ln z)2 dz		F(x)(ln x)2 dx	iR	F(Rei )(ln Rei	)2 ei d
r ,R	r		0
r		0
F (x)(ln x		2 i)2 dx ir	F (rei	)(ln rei )2 ei	d
R		2

I1 (r, R) I2 (R) I3 (r, R) I4 (r) .

Оценив интегралы I2 (R) и I4 (r) , получаем, что они стремятся к

нулю при

R

и r

0 соответственно (рекомендуем проде-

лать подробные выкладки самостоятельно). Далее,

R

R

I

1

(r, R) I

3

(r, R)

F (x)(ln x)2 dx

F (x)(ln x 2 i)2 dx

0

0

R

R

4

2 F (x)dx

4 i

F (x) ln xdx .

0

0

Переходя к пределу при R

и r

0 в представлении

I (r, R)

I

2

(R)

I

3

(r, R)

I

4

(r)

F(z)(ln z)2 dz ,

1

r ,R

приходим к равенству

k

4 2

F (x)dx

4

i

F (x) ln xdx

2

i

Res{F (z)(ln z)2 }.

0

0

j

1

z j

Отделяя вещественную и мнимую части, получаем формулы:

86

1

k

F (x) ln xdx

Im i

Res{F (z)(ln z)2 } ,

(3.3)

2

0

j

1

z j

1

k

F (x)dx

Re i

Res{F (z)(ln z)2 } .

(3.4)

2

0

j

1

z j

Замечание. В случае четной рациональной функции

F (z) для

вычисления

F (x) ln xdx

можно рассмотреть

интеграл

0

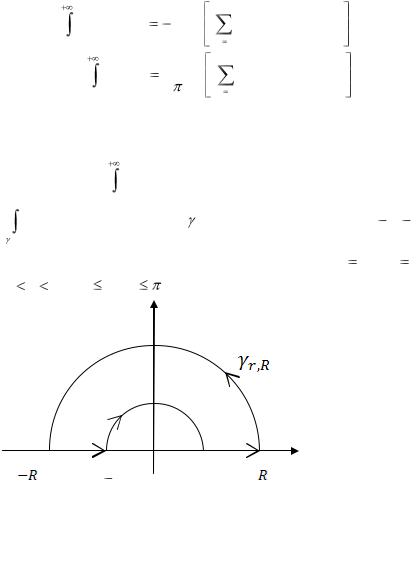
F (z) ln zdz ,

где контур

r , R состоит из отрезков

[

R;

r] ,

r ,R

[r; R] действительной оси

r ,

z

R ,

и

полуокружностей

z

0 r R , 0

arg z

(рис.55). Считаем, что внутри контура

лежат все полю-

сы функции F (z) ,

		находящиеся			в
		верхней полуплос-
		кости.		Опуская
		подробные вычис-
		ления	(вдумчивый
		читатель			без
		труда	восстано-
		вит	их	само-
r	r	стоятельно),			мы
		приведем			лишь
		формулы,			полу-
	Рис.55	чающиеся тем же
		методом,		что и
		выше:

87

F (x) ln xdx	Re i		Res{F (z) ln z} , (3.5)
0	Im z j	0	z j

F (x)dx 2 Im i		Res{F (z) ln z} .
0	Im z j 0	z j

Задача 22.

Вычислить

ln x dx

, где a и b – положитель-

0

(x a)2 b2

ные числа.

Решение.

В этом примере

F (z)

P(z)

1

имеет

Q(z) (z a)2

b2

простые полюсы z1,2

a bi , не попадающие на положительную

полуось; степень Q(z)

на 2 единицы больше степени многочлена

P(z) . Наконец,

2 }

(ln z )2

[n( a

bi)]2

Res {F (z)(ln z)

1

2(z1

a)

2bi

z1 a

bi

i

b

2

arctg

ln

a2

b2

i

,

2b

a

i

b

2

arctg

Res {F (z)(ln z)2 }

ln

a 2

b2

i

.

2b

a

z2 a bi

Следовательно,

Res{F (z)(ln z)2 }

Res{F (z)(ln z)2 }

1

(ln( a 2

b2 )

2

) arctg

b

.

z1

z2

b

a

Применяя формулу (3.3), имеем

88

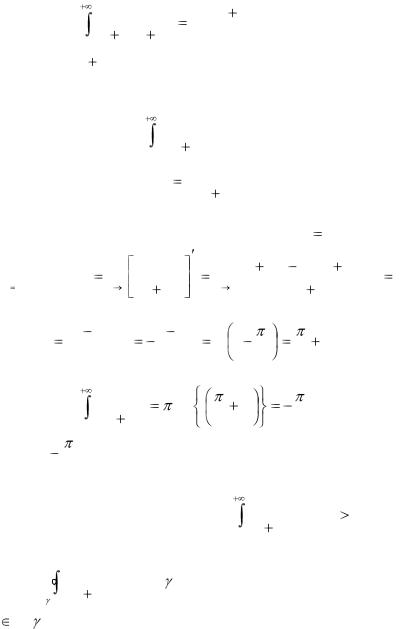
ln x dx

ln( a2

b2 )

arctg

b

.

0

(x a)2

b2

2b

a

Ответ.

ln( a2 b2 )

arctg

b

.

2b

a

ln xdx

Задача 23. Вычислить

.

(x2

1)2

0

Решение.

Функция F (z)

1

допускает применение

(z 2 1)

2

формулы (3.5). Лишь одна особая точка этой функции лежит в верхней полуплоскости – полюс второго порядка z1 i . При этом

Res{F (z) ln z}

lim

ln z

lim

(z i)2

2z(z i) ln z

(z i)2

z(z i)4

z1 i

z i

z i

2i

2i ln i

1 ln i

i

1

i

i

.

i(2i)3

4i

4

2

8

4

Согласно формуле (3.5)

ln xdx

Re i

i

.

0

(x2

1)2

8 4

4

Ответ.

.

4

Задача 24. (№ 4.191 [1])

Вычислить

ln 2 xdx

, где a 0 .

0

x2 a2

Решение. Введем в рассмотрение вспомогательный контурный

	интеграл	ln 2	z	dz , где		изображен на рис.55 и такой, что
		z2	a2		r , R

r ,R

ai int r ,R . По основной теореме теории вычетов

89

ln 2 z

ln 2

ai

2

dz 2

i

ln a

i

z 2

a 2

2ai

a

2

r , R

2

ln 2

a

i ln a .

a

4

Найдем этот же интеграл другим способом:

ln 2 z

dz

R

ln 2 x

dx

iR

ln 2

(Rei

)ei

d

z 2

a2

r

x2

a2

0

R2 e2i

a2

r , R

r (ln(

x)

)2

dx ir

0 ln 2 (rei

)ei

d .

R

x2

a 2

r 2 e2i

a 2

Как и при выводе формулы (3.3), показываем, что интегралы

iR

ln 2 (Rei

)ei

d

и ir

0

ln 2 (rei

)ei

d

стремятся к нулю, если

R2e2i

a2

r 2e2i

a2

0

R

, а r

0 . Кроме того,

R

ln 2 x

dx

r (ln(

x)

)

2

dx

R

ln 2 x

dx

r

x 2

a 2

R

x 2

a 2

r

x 2

a 2

r

(ln x

)2

dx

R

ln 2 x

(ln x

i)2

dx

R

x 2

a 2

r

x 2

a 2

R

ln 2

x

R

ln x

2 R

dx

2

dx

2

i

dx

.

x2

a2

x2 a2

x2

a2

r

r

r

Перейдем к пределу при R

и

r

0 в полученном равен-

стве

ln 2

a

2

i ln a

2R

ln 2 x

dx 2 iR

ln x

dx

x2

a 2

a

4

r

x2

a 2

r

2 R

dx

iR

ln 2 (Rei )ei

d

ir

0

ln 2 (rei )ei

d .

x2

a 2

R2 e2i

a 2

r 2 e2i

a 2

r

0

В результате приходим к представлению

90