Барменков Методика решения задач повышенной сложности по теории 2010

5)

Всякое дробно линейное отображение (ДЛО) верхней полу-

плоскости

С : {z : Im z

0}

на

единичный

круг

{w :

w

1} имеет вид

w

ei

z

a

,

z

a

где

Im a

0,

R .

6)

Всякое ДЛО единичного круга {z :

z

1} на себя имеет вид

w

ei

z

a

,

1

az

где

a

1.

7)

Для того чтобы ДЛФ w

az

b

отображала верхнюю полу-

cz

d

плоскость

С на себя, необходимо и достаточно, чтобы все

коэффициенты a,b,c,d были вещественными и ad bc

0 .

Рассмотрим различные типы задач на нахождение конформных отображений с помощью ДЛФ.

Задача 1. (№ 2.17(1) [1]) Найти ДЛФ w , переводящую точки 1, i , 1 i соответственно в точки 0 , 2i , 1 i .

Решение. Применяя указанную после свойства 2) формулу, получаем

w 0 1 i 2i

z 1 1

i i

.

w 2i 1 i 0 z i 1

i 1

Отсюда

z

1

1

w

1

3i

z

i 2

i

w 2i

1

i

и (z 1)(w 2i)(1 i)

w(z

i)(2

i)(1

3i) . Разрешив последнее

равенство относительно w , получим

11

w

2i(z 1)(1

i)

2iz

2i

.

(z

1)(1

i)

(z

i)(1

3i)(2

i)

4z

1

5i

Ответ. w

2iz

2i

.

4z

1

5i

Упражнение 3. Решить задачу 1, используя свойство 2) ДЛФ.

Задача 2. (№ 2.18(2) [1]) Найти ДЛФ, переводящую точки

1 ,

, i соответственно в точки

,

i ,

1.

Решение. Искомую ДЛФ запишем в виде w

az

b

. Так как

cz

d

w( 1)

, то

c (

1)

d

0 , т.е. c

d

и поэтому

w

az

b

.

c(z

1)

Отсюда следует, что c

0 . Поделив числитель и знаменатель на c ,

a

z

b

получаем

w

c

c

. Далее, поскольку w(

z

1

iz

b

w

c

. Так как еще по условию w(i) 1

z

1

i 2

b

b

ределения

уравнение:

1

c

, откуда

c

i

1

Окончательно имеем

w

iz

2 i

.

z

1

Ответ.

w

iz

2

i

.

z

1

	) i , то	a	i , т.е.
		c

, то получаем для оп-

	b	2 i .
	c

12

Задача 3. (№ 2.28(1) [1])

Найти ДЛФ w , отображающую верх-

нюю полуплоскость {z : Im z

0} на круг {w :

w

1} так, чтобы

w(i) 0 ,

arg w (i)

.

2

Решение. В силу свойства 5) ДЛФ

w будем искать в виде

w ei

z

a

, Im a

0. Используя первое условие задачи, полу-

z

a

чаем

0

e

i i

a

.

i

a

Отсюда,

a

i ,

a

i . Поэтому

w

ei

z

i

. Осталось найти

z

i

параметр

. Вычислим производную w . Имеем

w

e

i (z

i) (z i)

e

i

2i

.

(z

i)2

(z

i)2

В точке z

i

w (i)

ei

2i

ei

.

(2i)2

2i

Таким образом, arg w (i)

arg ei

arg( 2i)

. Учитывая

2

второе условие задачи, получаем

. Отсюда

0 , и

2

2

искомая ДЛФ имеет вид w

z

i

.

z

i

Ответ.

w

z

i

.

z

i

13

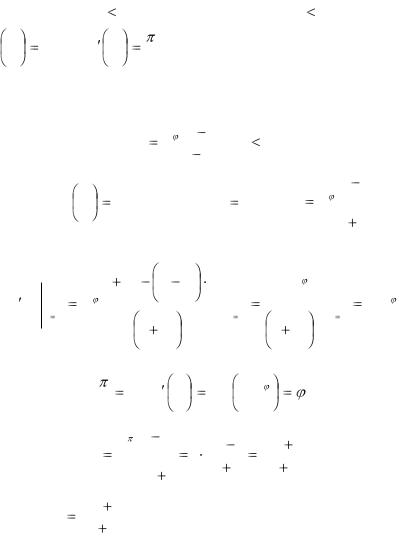
Задача 4. (№ 2.37(2) [1]) Найти ДЛФ w , отображающую еди-

ничный круг {z :			z		1} на единичный круг {w :				w	1} так, чтобы
w	i	0 , arg w			i			.
	2			2			2

Решение. Поступаем так же, как и при решении предыдущей задачи, но пользуемся уже свойством 6) ДЛФ. По этому свойству всякая ДЛФ, осуществляющая искомое отображение, имеет вид

		w ei	z	a	,		a			1 .
		1		az								z		i
	i								i
Из условия w		0 находим, что a								, т.е. w ei			2			.
	2					2					1		iz
													2

Далее,

w (z)

				1		iz		z			i		i							3		i
		e	i			2					2	2								4 e								4	e	i	.
z	i								iz 2							z	i					iz	2		z	i	3
	2						1										2	1								2
								2													2

Учитывая второе условие, получаем
		arg w	i	arg	4	e	i	.
2			2		3

							z		i
		ei											2z	i		2iz	1
									2									.
Таким образом, w				2								i
							iz		1				iz	2		iz	2
					2
Ответ. w	2iz	1	.
	iz	2

14

Задача 5. Найти ДЛФ w ,			отображающую верхнюю			полуплос-
	{z : Im z 0} на круг					w(1) i ,
кость			{w :	w	1} так, чтобы
w(i)	2 i	.
	5

Решение. Согласно теореме 2, ДЛФ, отображающая верхнюю

полуплоскость на единичный круг, границу

{z : Im z

0} этой по-

луплоскости отображает на границу {w :

w

1} единичного круга.

Точки i

и

i симметричны относительно вещественной оси, при-

чем точка

i отображается в точку

1

(2 i) . По свойству 4) ДЛФ

5

точка

i

перейдет в точку a , симметричную точке

1

(2

i) отно-

5

1} . Найдем точку a , исходя из ус-

сительно окружности {w :

w

ловий

симметрии

относительно

окружности:

1

i

a

1

и

2

5

arg

2

i

arg a . Из первого условия получим

a

5 . Второе

5

условие дает a

(2 i) с некоторым положительным числом .

2

i

1

a

2

i .

На

основании

равенства

a

имеем

и

Итак,

искомая ДЛФ подчинена условиям:

w(1)

i ,

w(i)

2

i

,

5

w(

i)

2

i .

По

схеме

решения

задачи 1

находим,

что

w

(2

i)z 5i

.

(2i

1)z

4i

3

Проверим, что найденная нами функция действительно отображает верхнюю полуплоскость на единичный круг. Для этого доста-

	точно записать полученную функцию в виде w	i	z	(1	2i)	и
			z	(1	2i)

применить свойство 5) ДЛФ.

15

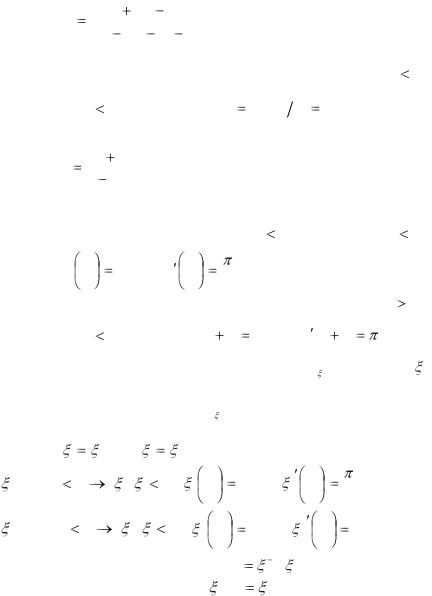
Ответ. w

(2 i)z 5i

.

(2i 1)z 4i

3

Упражнение 4.

Найти ДЛФ w , отображающую круг {z :

z

1}

1} так, чтобы w(i)

i ,

w(i 2)

4i

.

на круг {w :

w

5

Указание. Воспользоваться свойствами 4) и 6) ДЛФ.

Ответ. w

2z

i

.

2

iz

Упражнение 5. Найти:

а) ДЛФ w , отображающую круг {z :

z

1} на круг {w :

w

1}

так, что w

1

1

, arg w

1

;

2

2

2

2

б) ДЛФ w , отображающую верхнюю полуплоскость {z : Im z

0}

1} так, что w (1

i)

1

, arg w (1 i)

на круг {w :

w

.

2

Указание. Ввести промежуточную плоскость С

переменного

и отобразить фигурирующие в условии упражнения 5 области на некоторую область плоскости С , взяв затем подходящую суперпозицию отображений. Например, для решения части а) находят

две ДЛФ

1(z)

и

2 (w) , удовлетворяющие условиям:

1 :{z :

z

1}

{

:

1},

1

1

0

, arg

1

1

;

2

2

2

2 :{w :

w

1}

{

:

1} ,

2

1

0 , arg

2

1

0 .

2

2

1 (

Тогда искомая

ДЛФ

имеет

вид w

1

(z)) .

На практике

2

обычно записывают равенство

1 (z)

2 (w)

и из него выража-

ют w через z .

16

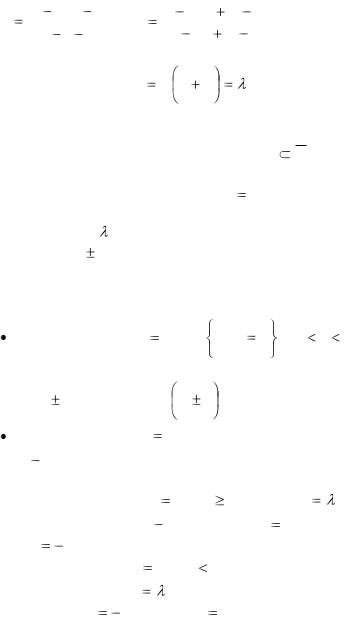
Ответ. а) w	(5 3i)z 4	; б) w		(1		2i)z		3i 3	.
	4z 5 3i
				(2 i)z 3i 3
1.3. Функция Жуковского w				1		z	1	(z) .
				2			z

Перечислим ее основные свойства.

1) Функция Жуковского однолистна в области D С z тогда и только тогда, когда D не содержит ни одной пары точек z1 и z2 , связанных соотношением z1 z2 1.

2)Отображение w (z) конформно в любой точке, отличной от точек z 1.

3)При отображении функцией Жуковского:

		r} и z :		z		1		, 0 r 1,
окружности {z :	z
							r

переходят в один и тот же эллипс с фокусами в точ-

ках 1 и полуосями

1

1

r

;

2

r

окружность

{z :

z

1}

отобразится

на

отрезок

[

1;1] , проходимый дважды;

при этом, когда точка

z

пробегает против часовой стрелки верхнюю по-

0} , точка w

(z)

луокружность {z :

z

1, Im z

пробегает отрезок [

1;1]

от точки w

1 до точки

w

1; когда же

z

пробегает нижнюю полуок-

ружность {z :

z

1, Im z 0} против часовой

стрелки, точка w

(z) пробегает тот же отрезок

от точки w

1 до точки w

1;

17

лучи	[0;	]	и [	;0]	переходят соответственно
в лучи [1;		] и [		; 1] , проходимые дважды. Ес-
ли z	пробегает луч [0;				] , то когда z	возрастает
от 0 до 1, w				(z) проходит луч [1;		] справа
налево, а когда			z возрастает от 1 до			, то точка

wпробегает этот же луч слева направо.

4)Функция Жуковского конформно отображает:

круг		{z :	z	r} (так же, как и	внешность
{z :	z	r} его замыкания) на всю			плоскость с
разрезом по отрезку [ 1;1] (рис.5).

w

i z

w = λ(z)

1

-1

1

Рис.5

18

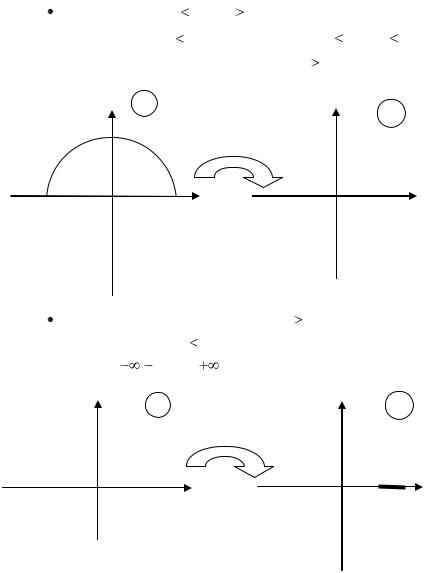
полукруг {z :	z	1, Im z 0} на	нижнюю полуплос-
кость {w : Im w		0} , а полукруг
			{z :	z	1, Im z 0} –
на верхнюю полуплоскость {w : Im w 0} (рис.6);
z					w
		w = λ(z)
-1		1

Рис.6

верхнюю полуплоскость {z : Im z 0} (так же, как и

нижнюю {z : Im z	0} ) на плоскость Сw			с разрезом по
лучам [ ; 1] и [1;	] (рис.7).
z	w = λ(z)			w
		-1		1

Рис.7

19

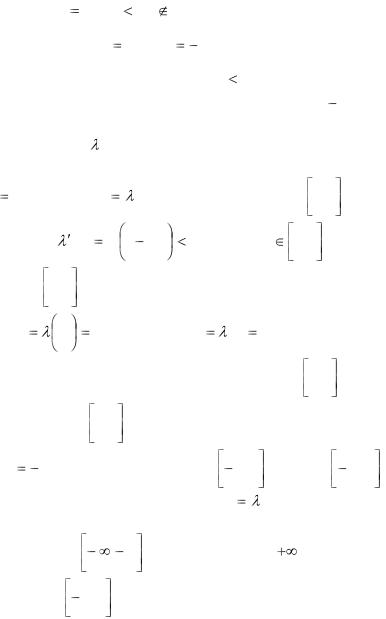
	Задача 6. (№ 2.112 [1])				Найти образ лежащей в единичном кру-
	ге области D {z :	z		1, z		[c;1]} при отображении функцией
	Жуковского, если а) c			1	; б) c		1	.
			2				2
	Решение. По свойству 4)					круг {z :			z	1} отобразится функцией

Жуковского на всю плоскость с разрезом по отрезку [ 1;1] . Обозначим эту область через G1 . Найдем образ промежутка [c;1] при отображении w (z) и исключим его из области G1 . Это и будет искомая область. Случаи а) и б) рассмотрим отдельно.

а) c		1		. Функция w														(z) непрерывна на отрезке											1		;1	, а ее
	2																										2
производная										(x)					1		1		1	0 для всех				x		1	;1				. Значит,
															2				x 2						2
на отрезке						1			;1		функция Жуковского монотонно убывает от зна-
						2
чения w								1				5			до значения w						(1)			1 , принимая все про-
						2					4
межуточные значения. Таким образом, промежуток																												1		;1		перей-
																											2
дет в промежуток											1;				5	.
															4
б)	c				1		. Разобьем промежуток															1	;1		на два:								1	;0	и
				2																	2											2
[0;1] , на каждом из которых функция w																								(z) непрерывна и мо-

нотонна. Действуя как в случае а), показываем, что первый отрезок

	переходит в луч		;	5	, а второй – в луч [1; ] . Поэтому весь
				4
	промежуток	1	;1	переходит в объединение двух лучей
		2
					20