Барменков Методика решения задач повышенной сложности по теории 2010

z

k

2z

k

2

2k 2

1)k 2

2k 2 .

Res f (z)

(

(sin

zk )

cos

zk

2

2

zk

cos k

z

k

k

2

r

4

2 , попадает один про-

Внутрь контура

r

{z :

z

r} ,

стой

полюс

z1

2

подынтегральной

функции f (z) .

Итак,

z

dz

2

i Res f (z)

2

i(

2

2 )

4

3i .

sin

z

2

r

Ответ. б)

4

3i .

r

в) В области

int

r

{z :

z

r}

при

40 находятся два про-

стых полюса

z

2 ,

z

2

4

2

подынтегральной функции. Значит,

1

z

dz

2

i{Res f (z)

Res f (z)}

2

i(

2 2

8 2 )

12 3i.

r sin

z

2

4

2

Ответ. в)

12

3i .

Задача 17. Вычислить

dz

в каждом из сле-

sin 3z(1

cos 2z)

r

дующих случаев:

а) 0 r

, б)

r

2

, в) r 2 .

3

3

3

Решение.

Функция

sin 3z

обращается в нуль только в точках

zk

k ,

k

Z,

причем каждый из этих нулей простой. Все нули

3

функции 1

cos 2z суть точки z3n

n, n

Z (проверьте, что каж-

дый из этих нулей имеет кратность, равную двум). Таким образом, подынтегральная функция имеет простые полюсы в точках

71

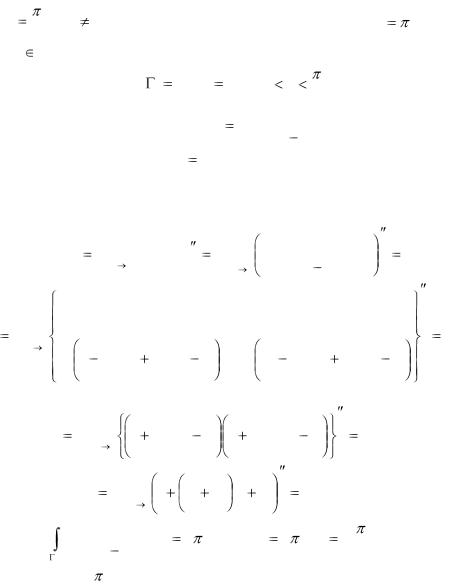
zk

k , k 3n , и полюсы третьего порядка в точках

z3n

n ,

3

k, n

Z .

r} , 0 r

а)

Внутри контура

r

{z :

z

, лежит только

3

одна особая точка функции

f (z)

1

,

а именно,

sin 3z(1

cos 2z)

полюс третьего порядка

z0

0 .

Непосредственное применение

формулы для вычисления вычета в этой точке приводит к громоздким выкладкам, если не воспользоваться приемом разложения в степенные ряды (см. задачу 15).

	Res f (z)								1			lim ( f (z)z 3 )												1		lim								z 3
		0							2! z					0								2!				z 0 sin 3z(1										cos 2z)
1		lim																								z3
										(3z)2							(3z)4										2 1 (2z)2											(2z)4
	2! z 0
				3z 1																		... (2z)																		...
										3!							5!											2!				4!				6!
							1		lim					1			(3z)2					... 1						2(2z)2				...
					12 z					0							3!											4!
										1					lim		1		9			8				z2 ....							11		.
												12 z 0							3!			4!										36
Итак,										dz									2			i Res f (z) 2										i		11			11 i		.
					sin 3z(1 cos 2z)																	0										36				18
			r
Ответ. а)							11			i		.
							18
																						72

	б)		Область int												r				{z :					z				r} при															r				2						содержит кроме
																																						3									3
полюса третьего порядка z0																												0 еще два простых полюса z1																																	и
																																																												3
z-1							функции										f (z) . Найдем вычеты в них:
			3
									Res f (z)																								1																					2		.
																			{sin 3z(1														cos 2z)}													z								9
										3
																																															3
Отсюда
									dz										2							i(Res f (z)															Res f (z) Res f (z))
			sin 3z(1								cos 2z)
																																							0
		r																									3																											3
															2					i(					2		11								2		)		5								i			.
																									9		36						9						18
Ответ.								б)					5		i		.
												18
В случае в)										к особым точкам z 1																																	, z0							0, z1									, лежащим
																																							3															3
внутри контура												2						{z :				z					2}, добавляются ещѐ два простых по-
люса						z 2						2				,						z2					2									подынтегральной																							функции
												3															3
f (z)												1									.					Найдем вычеты в указанных точках:
					sin 3z(1									cos 2z)
Res f (z)																			1																					2		.
								{sin 3z(1											cos 2z)}											z			2						9
2
3
																																	3
	Ответ.								в)			11				i		.
													18

73

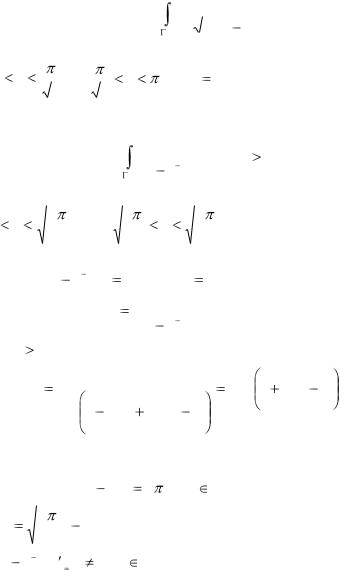
Упражнение 9. Вычислить

dz

в каждом из

sin

3z(1

cos 2z)

r

следующих случаев:

а) 0 r

, б)

r

, в) r 4 .

3

3

Задача 18. Вычислить

dz

, где

h 0 , в следующих слу-

z(1

e hz 2 )

r

чаях:

а) 0 r

2

,

б)

2

r

4

.

h

h

h

Решение. Особые точки подынтегральной функции находятся из

уравнения

z(1

e hz2 )

0 . Точка z

0 является полюсом третьего

порядка функции

f (z)

1

, поскольку при достаточно

z(1

e hz 2 )

малых

z

0 справедливо представление

1

1

hz2

f (z)

1

... .

z3h 1

hz

2

h

2

z

4

...

hz3

2!

2!

3!

Остальные изолированные особые точки f (z)

будут ее простыми

полюсами и находятся из формулы

hz

2

2 ki , k

Z \ {0},

k

т.е. zk

2 k

(

i) .

Проверьте последнее утверждение, показав,

h

что (1

e

hz 2 )

z

z

0,

k

Z \ {0}.

k

74

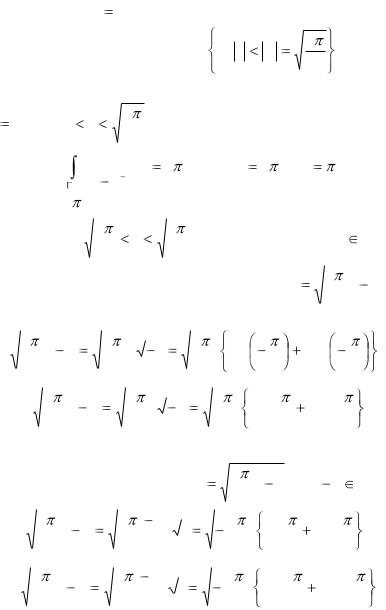
а) Очевидно, z0 0 – единственная изолированная особая точка

2

функции f (z) , попавшая в круг z : z z1 . Используя

h

полученное выше разложение f (z) в ряд Лорана в окрестности

z 0 ,

при 0

r

2

получаем

h

dz

2

i Res f (z)

2

i

h

i .

hz2

2!h

z(1

e

)

0

r

Ответ.

а)

i .

В случае б)

2

r

4

рассмотрим сначала

k

N. Вы-

h

h

пишем

значения

ветвей

квадратного корня

zk

2

k

( i) при

h

этих k :

2 k

2

k

2 k

cos

( i)

i

i sin

и

h

h

(0)

h

4

4

(0)

2 k

2 k

2 k

3

3

.

(

i)

i

cos

i sin

h

h

(1)

h

4

4

(1)

Эти точки лежат на биссектрисах второго и четвѐртого квадрантов.

Теперь рассмотрим значения zk

2 k

( i)

при

k

N:

h

2 k

2

(

k)

2

k

( i)

i

cos

i sin

и

h

h

h

4

4

(0)

(0)

2 k

2

(

k)

2

k

5

5

.

( i)

i

cos

i sin

h

h

(1)

h

4

4

(1)

Эти точки лежат на биссектрисах первого и третьего квадрантов.

75

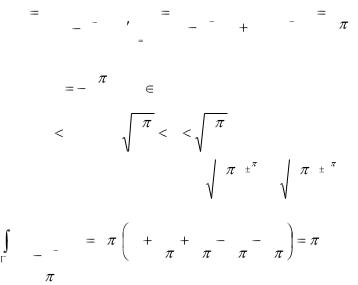
Заметим, что

Res f (z)

1

1

i

hz2

hzk2

2

hzk2

4 k

z

{z(1 e

)}

(1 e

k

) 2hzk e

z

zk

независимо от k и выбора ветви квадратного корня в формуле для

	zk , поскольку zk2	2 ki	, k Z \ {0}.
		h

В круг {z :

z

r}

при

2

r

4

попадают лишь пять

h

h

i

3

i

2

2

особых точек f (z) , а именно, точки 0,

e 4

,

e 4

. По-

h

h

этому для указанных r имеем

dz

2 i

1

i

i

i

i

i .

r z(1 e hz2 )

2 4

4

4

4

Ответ. б)

i .

76

3.Вычисление несобственных интегралов

3.1.Лемма Жордана и связанные с ней интегралы

В работе [2] показано, как методы комплексного анализа применяются к вычислению несобственных интегралов от вещественных функций. В этом разделе будут рассмотрены задачи повышенной сложности, связанные с нахождением несобственных интегралов.

При вычислении интегралов вида

f (x)dx ключевую роль иг-

рает следующее утверждение.

Лемма

Жордана.

Пусть

f (z)

непрерывна

на множестве

a

и на этом множестве f (z)

0

{z :

z

R0 , Im z

a},

0 ,

при z

. Тогда для любого b 0 имеем lim

eibz f (z)dz

0 ,

R

C R

где CR

– дуга окружности

z

R , лежащая в рассматриваемом

множестве.

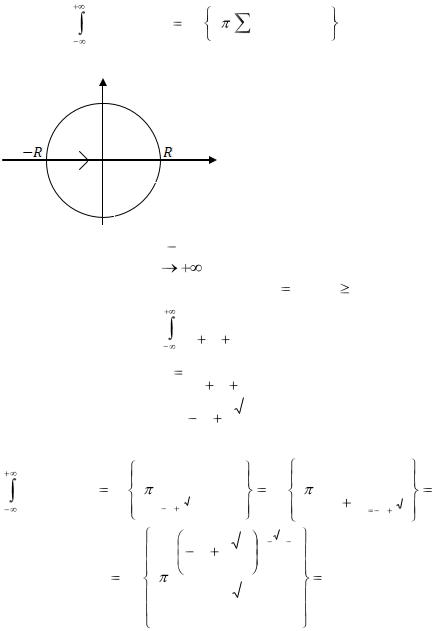
Укажем получаемые применением леммы Жордана формулы, позволяющие находить интегралы вида

R(x)sin axdx, R(x) cos axdx, a 0,

P(z)

где R(z) – рациональная функция, причем степень мно-

Q(z)

гочлена Q(z) , по крайней мере, на единицу больше степени P(z) , и на вещественной оси Q(x) 0 и Im R(x) 0 (последнее условие заведомо выполняется, если все коэффициенты многочленов P(z) и Q(z) вещественные). Именно, справедливы равенства

R(x) cos axdx Re 2 i Res R(z)eiaz ,	(3.1)
ak

77

R(x) sin axdx

Im

2

i

Res R(z)eiaz

,

(3.2)

ak

где

суммирование

ведется по

всем

полюсам

ak

функции

R(z) , лежащим в верхней по-

луплоскости (их, очевидно,

конечное число). Эти формулы

получаются

применением

ос-

Рис.51

новной теоремы

о

вычетах к

интегралу

от

функции

R(z)eiaz , взятому по вспомога-

тельному контуру СR [ R; R]

(рис.51) с последующим предель-

ным переходом

при R

,

использующим

лемму Жордана.

Здесь СR – верхняя полуокружность {z :

z

R, Im z

0} .

Задача 19. Вычислить

x cos x

dx .

x2

x

1

Решение. Функция R(z)

z

имеет в верхней полуплос-

z2

z

1

кости один простой полюс

1

i

3

,

поэтому указанная выше

2

2

формула (3.1) дает

R(x) cos xdx

Re 2 i Res R(z)eiz

Re

2

i

zeiz

1

3

2z

1

1

3

i

z

i

2

2

2

2

3

i

1

3

i

e

2

2

Re 2 i

2

2

i 3

78

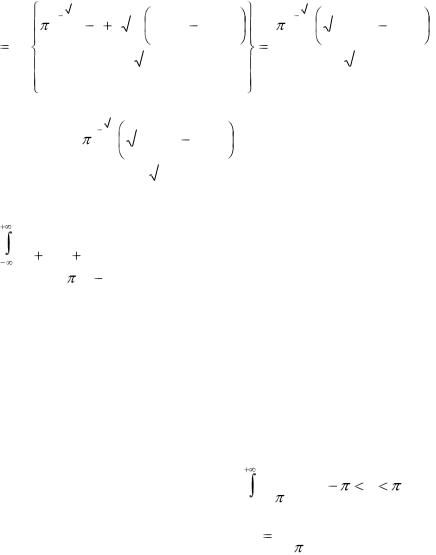
					3																1					1							3						1		1
		e 2				( 1				i			3) cos										i sin								e 2				3 sin					cos
Re																				2						2													2		2		.
													3																					3
									3											1				1
							e		2					3 sin									cos
Ответ.																				2			2				.
													3
Упражнение									10.				Используя формулу																	(3.2),				найти					интеграл
	x3 sin x							dx .
	x4 5x2						4
Ответ.						(4			e)			.
							3e2

Важной и полезной в приложениях леммой Жордана, разумеется, не исчерпывается все многообразие методов теории вычетов, применяемых при вычислении несобственных интегралов. В большинстве случаев приходится преодолевать две основные трудности, связанные с выбором вспомогательного контура интегрирования и поиском подходящей подынтегральной функции. В общей ситуации нет четких алгоритмов для решения обеих проблем. Мы приведем лишь некоторые примеры несобственных интегралов, не принадлежащих рассмотренному выше типу.

Задача 20.	(№ 4.205 [1]) Вычислить	ch ax		dx ,		a	.
	0	ch	x
	Рассмотрим функцию f (z)		eaz
Решение.					, которая и будет
			ch z

помещена под знак вспомогательного контурного интеграла. Найдѐм особые точки этой функции, решив уравнение

79

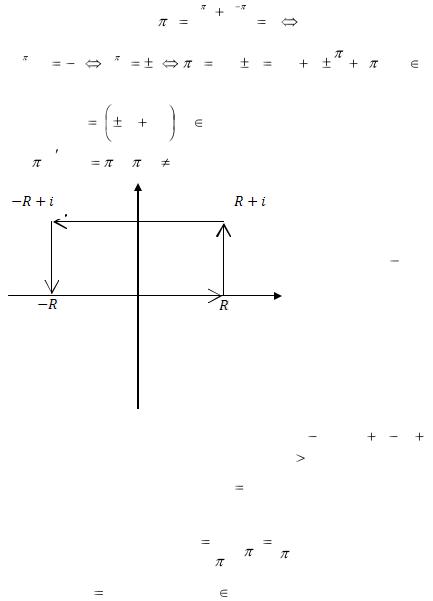
ch

z

e z

e

z

0

2

(e z )2

1

e z

i

z

Ln(

i)

ln 1 i(

2 k ), k Z

2

.

Итак,

zk

i

1

2k

, k Z ,

–

простые

(поскольку

2

(ch z) (zk )

sh zk 0 ) полюсы функции

Рис.52

f (z) .

Так как все особые точки zk ле-

жат на мнимой оси, то контур ви-

да СR [ R; R]

при неограниченном возрастании R будет содержать внутри себя всѐ большее число особых точек. Поэтому в качестве

вспомогательного контура выберем

прямоугольник

PR

с вершинами в

точках

R, R, R i, R i

(рис.52). Этот прямоугольник при любом R

0 содержит внутри

себя только один простой полюс z0

i

функции f (z) . При этом,

2

ai

ai

Res f (z)

e 2

e 2

,

i

i

i

sh

2

2

так как sh iz

isin z

для всех z

С. По основной теореме теории

вычетов

80