Мирошин Интегралные и дифференциалные операторы 2010

Доказательство. Дифференцируя X (t ) , имеем: dtd X (t ) = AetAX0 = AX (t ) , X (0)= X0 .

4.3. Фазовое пространство, фазовый поток, фазовые кривые

Определение 4.6. Рассмотрим систему

i

X = AX, X =(x ,..., x )T .

(4.2)

1

n

Тогда пространство En

называется фазовым пространством

этой системы, точки En – фазовые.

Определение 4.7. Пара

(En, {etA}t R )

называется фазовым по-

током.

Определение 4.8. Кривая в

En X (t )=etAX

0

называется фазо-

вой, проходящей через точку

X0 En. Фазовая кривая – это фазо-

вая траектория точки X0 под действием группы {etA}.

Определение 4.9. Точка

X

0

En

называется положением рав-

i

новесия системы X = AX

(неподвижной точкой фазового потока),

i

если t R

X (t)= etAX

0

≡ X

0

.

Замечание.

Для рассматриваемого случая X0 = 0 – неподвиж-

ная точка.

En+1 = E1 ×En ={(t, X )},

Определение 4.10. Пространство

где

En – фазовое пространство системы (4,2), называется расширен-

ным фазовым пространством системы (4.2).

График X (t )=etAX0 в расширенном фазовом пространстве на-

зывается интегральной кривой потока (En,{etA}) (системы 4.2).

31

4.4. Фазовые траектории на плоскости

Рассмотрим систему двух линейных уравнений с постоянными коэффициентами с двумя искомыми функциями:

i	a b			x
x = ax +by			,		(4.3)
	A =			X = .
i	c	d		y
y = cx +dy,

Фазовое пространство в этом случае двумерно – фазовая плоскость, соответствующая группа фазового потока {etA}, где

a	b	Исследуем в этом случае все фазовые траектории.
A =	.
c	d
Сразу отметим, что при любой матрице A точка			X0		0		является
				=	0

положением равновесия системы. Поведение кривых будет определяться корнями характеристического уравнения:

det (A −λE) ≡		a −λ	b		= 0 .
		c	d −λ

Пусть λ1 и λ2 – корни этого уравнения. Возможны следующие случаи.

I.= det A ≠ 0 λ1 ≠ 0 , λ2 ≠ 0 .

а) λ1 ≠ λ2

– вещественные. Общее решение

x

α1

λ t

α2

λ t

,

= C1

e 1

+C2

e

2

y

β1

β2

где

h =

α

,

h

=

α

2

– два линейно независимых собственных

1

β

1

β

2

2

1

вектора матрицы A (рис. 4.1).

1. λ1 < λ2 < 0 . Рассмотрим на фазовой плоскости 0xy прямые, проходящие через начало координат в направлении собственных

векторов h1 = (α1, β1 ) и h2 = (α2, β2 ) матрицы A. Эти прямые сами являются фазовыми траекториями:

32

t → +∞ ,

C ≠ 0, C		2	= 0		y	=	β1	,	C = 0, C		2	≠ 0		y	=	β1	.
1					x		α1		1					x		α1
Строим эти траектории. Далее, если t → +∞ , то:
x (t) = C α eλ1t +C				α eλ2t →0 ,					y (t) =C β eλ1t				+C β eλ2t →0 ,
1	1		2	2					1	1			2	2

т.е. при t → +∞ по любой траектории точка движется в начало координат. Считаем производную y′x :

y′x =

y′t

C1β1λ1eλ1t

+C2β2λ2eλ2t

C1β1λ1e(λ1−λ2)t

+C2β2λ2

=

=

.

′

C1α1λ1e

λ1t

+C2α2λ2e

λ2t

C1α1λ1e

(λ1−λ2)t

+C2α2λ

2

xt

При t → +∞ y′x →β2 / α2 , это означает, что при t → +∞ все траектории входят в начало координат, касаясь прямой с направляющим вектором h2 (отвечающим меньшему по модулю собственному значению матрицы A). Если же t → −∞ , то y′x →β1 / α1 . Это означает, что на « −∞» фазовые траектории имеют асимптоты, параллельные прямой с направляющим вектором h1 ={α1, β1} (отве-

чающим большему по абсолютной величине собственному значению A). Кроме того, точка O (0, 0) – сама является фазовой тра-

екторией. Это положение равновесия, которое называется устойчивым узлом (см. рис 4.1, а).

2. 0 <λ2 <λ1 . В этом случае замена t → −t сводит рассматри-

ваемые траектории к траекториям пункта 1. Начертание фазовых траекторий не изменится (см. рис 4.1, б), но направление движения точки по траектории с возрастанием t сменится на противоположное. O (0, 0) – точка покоя, в этом случае положение равновесия −

неустойчивый узел.

3. λ1 <0 <λ2 . В этом случае: y′x →β2 / α2 при

y′x →β1 / α1 при t → −∞ . O (0, 0) – точки покоя. Она называется

седлом (см. рис 4.1, в).

б) λ1 ≠ λ2 – комплексные. Тогда λ2 =λ1 = α+iβ.

Общее решение имеет вид:

x(t )=(C1 cosβt +C2 sin βt)eαt;y (t)=(C1 cosβt +C2 sin βt )eαt,

33

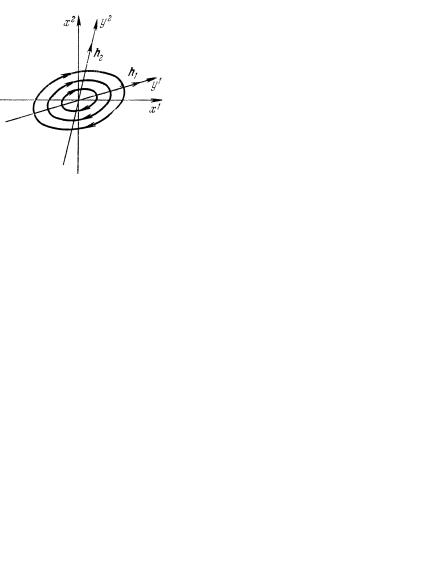
где C1 и C2 – произвольные постоянные, а C1 и C2 – их линейные комбинации. Возможны следующие случаи (рис. 4.2).

а

б

в

Рис. 4.1. Фазовые траектории вблизи точки равновесия в случае действительных, отличных от нуля собственных значений λ1 ≠ λ2 :

а – устойчивый узел; б – неустойчивый узел; в – «седло»

34

1. α =0 . Тогда

(

C x −C y =

C C

2

−C C

sin βt;

1

1

1

2 1)

x −C

y =(C C

−C C

)cosβt,

C

2

2

2

2

1

1

т.е. получаем семейство кривых

(C1x −C1y)2

(C2x −C2 y)2

+

=1.

(C1C2 −C2C1)2

(C1C2 −C2C1)2

В этом случае точка покоя

O (0, 0)

называется центром (см.

рис. 4.2, а).

Центр – траектория, устойчивая по Ляпунову, но не асимпто-

тически устойчивая. Все траектории центра замкнутые. Для того чтобы найти направления движения по этим траекториям, нужно

взять точку M0 (x0,	y0 ),	подсчитать вектор скорости V (x, y) в
этой точке M0 (x0, y0 ) из системы (4.3).
i	i
Имеем: V = x (t)	, y (t)			={ax +by, cx +dy}	.
		M0			M0

Замечательное свойство поля скоростей V (t ): так как точка покоя только одна (точка O (0, 0)) и V (t ) непрерывно зависит от

M (x, y), то вдоль любой траектории направление движения не меняется, на всех траекториях направление движения одинаково!

2. α ≠ 0 . Аналогичные выкладки дают:
	(C1x −C1y)2	+	(C2x −C2 y)2		= e	2αt	.
	(C1C2 −C2C1)2		(C1C2 −C2C1)	2
В этом случае точка покоя			O (0, 0) называется фокусом. Если

α <0 , то при t → +∞ точка по любой траектории неограниченно приближается к точке O (0, 0), т.е. при α <0 фокус асимптотически устойчив (см. рис. 4.2, б). Если же α > 0 , то при t → +∞ точка по любой траектории уходит на бесконечность, т.е. при α > 0 точка O (0, 0) неустойчива – неустойчивый фокус (см. рис. 4.2, б).

в) λ1 = λ2 ≠ 0 (так как ≠0) . В этом случае λ1 и λ2 – обязательно вещественные числа. Возможны следующие случаи.

35

а

б

в

Рис. 4.2. Фазовые траектории вблизи точки равновесия в случае комплексных собственных значений λ1 ≠ λ2 :

а – центр; б – устойчивый фокус; в – неустойчивый фокус

36

1. λ1 = λ2 = λ ≠ 0 ,		Rang (A−λE) = 0 , т.е.		A −λE = O – нулевая
матрица. Но тогда исходная система (4.3) имеет вид:
x = λx;		x (t ) =C eλt,	y (t ) =C eλt,		C , C		R .
						2
y = λy,		1	2		1

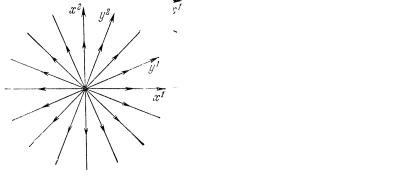
Фазовые траектории – всевозможные полупрямые, исходящие из начала координат. Точка покоя O (0, 0) в этом случае называется

дикритическим узлом (рис. 4.3).

а

б

Рис. 4.3. Фазовые траектории вблизи точки равновесия в случае действительных собственных значений λ1 = λ2 (дикритический узел):

а – устойчивый; б – неустойчивый

Если λ < 0 , то дикритический узел асимптотически устойчив

(см. рис.4.3, а), если λ > 0 – то неустойчив (см. рис.4.3, б).

2. λ1 = λ2 = λ ≠ 0 , Rang (A −λE) =1. Общее решение имеет вид

x(t)				α		+C2		α		+α t
		= C1		1					2	3 eλt,
y (t)				β1				β2 +β3t
где h1 ={α1, β1} –		собственный						вектор, а h2 ={α2, β2},

h3 ={α3, β3} – некоторые векторы. Уточним структуру решения, имеем:

37

				′
C1 h1+C2		h2 +h3 t eλt = A C1 h1 +C2					h2 +h3 t
	↓	↓	↓			↓	↓	↓
приравнивая коэффициенты при					t eλt,	получаем: λh =
								3

↓

eλt,

Ah3 , т.е.

↓

h3 – собственный вектор A. Тогда h3						h1 . Следовательно, меняя
↓					↓	↓
константы, можно считать, что h3				= h1 (!).
Получили общее решение			↓		↓
x (t)								λt	.
		= C1 h1+C2			h2	+h1 t e
y (t)			↓		↓ ↓

Точка покоя O (0, 0) в этом случае называется вырожденным узлом (рис. 4.4). Если λ < 0 , то вырожденный узел асимптотически ус-

тойчив (см. рис. 4.4, а), а если λ > 0 – то неустойчив (см.

рис. 4.4, б). Среди фазовых траекторий имеется одна прямолинейная

–y = β1 , т.е. траектория в направлении собственного вектора h1 . x α1

Далее имеем:
y′x =	C2β1 +λ(C1β1 +C2	(β2 +β1t ))	→		β1	при t →∞.
	C2α1 +λ(C1α1 +C2
		(ε2 +α1t ))			α1
Следовательно, при λ<0 все траектории входят в точку O (0, 0),
при t → +∞ касаясь прямой y = (β1 / α1)x ,				и уходят из "−∞" под

этим же углом (аналогично при λ>0) . Для уточнения хода траекторий строятся несколько векторов поля скоростей.

II. Рассмотрим случай	=		a	b		= 0 . В этом случае хотя бы
			c	d

один из корней характеристического уравнения равен нулю (а следовательно, оба корня действительны).

а) λ1 = 0, λ2 ≠ 0. Общее решение:

x

= C

α

+C

α

2

et

λ

2

,

1

2

1

β1

β2

y

38

где h1 ={α1, β2}	и h2 ={α2, β2}	– собственные векторы матрицы A.
Если C2 = 0 ,	C1 ≠ 0 , то	получаем фазовую траекторию

y = (β1 / α1)x . На этой траектории каждая точка – точка покоя!
Все остальные траектории (C2 ≠ 0) – также прямолинейные
	y −C1β1			=	β2		.
	x −C α				α	2
1		1
Все они параллельны вектору h2 .				При λ < 0 точки по этим траек-
ториям “движутся” к прямой		y = (β1 / α1)x . При λ < 0 все точки

покоя устойчивы по Ляпунову (но не асимптотически), при λ > 0 –

неустойчивы.

а б

Рис. 4.4. Фазовые траектории вблизи точки равновесия в случае действительных собственных значений λ1 =λ2 =λ ≠ 0

(вырожденный узел): а – устойчивый; б– неустойчивый

б) λ1 = λ2 = 0 . В этом случае возможны следующие ситуации.

1. Rang (A −0E) = 0 . Тогда	A =O – нулевая матрица. Общее
решение x (t ) = C1 , y (t) =C2 .	Каждая точка плоскости – точка

покоя, устойчивая по Ляпунову, но не асимптотически.

39

2. Rang (A −0E) =1. Общее решение
x(t )		=C1		α		+C2		α		+α t	,
				1					2	3
y (t)				β1				β2 +β3t

где h1 ={α1, β2}	– собственный вектор. Вновь показываем, что
h3 ={α3, β3} = h1 .	Среди траекторий имеется (C2 = 0, C1 ≠ 0)

траектория y = (β1 / α1)x , целиком состоящая из точек покоя. Остальные траектории – прямые, параллельные прямой y = (β1 / α1)x :

	y −C1β1 −C2β2					=	β1	.
	x −C α −C α			2			α
	1	1	2				1
Поле скоростей V (t)	i		i			= C h			меняет направление
	= x	(t), y (t)
							2	1

при изменении знака C2 . Точка O (0,0) и другие положения равно-

весия неустойчивы.

Были рассмотрены всевозможные виды фазовых траекторий в этом простейшем случае.

§ 5. Первые интегралы системы ОДУ

Вновь рассматриваем систему ОДУ
y ' = f (t, y) ,	(5.1)
где y = (y1,..., yn ), f = ( f1 (t, y),..., fn (t, y))	– непрерывно диффе-

ренцируемая в некоторой области G Etn,y+1 вектор-функция.

Определение 5.1. Функция ψ(t, y), удовлетворяющая в некоторой подобласти G ' ≤ G условиям:

1)ψ(t, y) непрерывно дифференцируема в G ' и не равна в G ' тождественно постоянной;

2)ψ(t, y) ≡ const вдоль любого решения y = y (t) системы (5.1),

проходящего в G ' , называется первым интегралом системы (5.1) в

G ' .

40