Шведенко Начала анализа функций комплексной переменной 2008

										101
T. E. PARAMETRI^ESKOMU ZADANI@ \LLIPSOW NA PLOSKOSTI PE-
	1	;	1			1	;	1
REMENNOJ w =u+iv S POLUOSQMI 2					I	2				| cOOT-
		r + r					r ; r
WETSTWENNO NA ee DEJSTWITELXNOJ I MNIMOJ OSQH										(RIS. 31

STRELKI UKAZYWA@T NAPRAWLENIE DWIVENIQ TO^EK PRI WOZRASTANII PARAMETRA t).

rIS. 31

sOOTWETSTWIE MEVDU TO^KAMI UKAZANNYH OKRUVNOSTEJ

I \LLIPSOW QWLQETSQ WZAIMNO ODNOZNA^NYM, A W SOWOKUPNOS-

TI \TI \LLIPSY ZAPOLNQ@T WS@ PLOSKOSTX C ZA ISKL@^E-

NIEM OTREZKA [;1 1]. oBRAZ PLOSKOSTI (KAK C , TAK I C )

PEREMENNOJ z S \PROREHOJ" W WIDE KRUGA jzj 6 1 ESTX PO- \TOMU WSQ PLOSKOSTX (SOOTWETSTWENNO C I C ) PEREMENNOJ

102

w c \RAZREZOM" PO OTREZKU [;1 1] (ZNA^ENI@ z =1 SOOT- WETSTWUET w=1).

zAMENA z NA 1z NE MENQET FUNKCII w = 12;z + z1 , NO PE- REWODIT TO^KU 1 W TO^KU 0, a OKRUVNOSTI RADIUSOW r > 1

(S CENTROM z =0) | W KONCENTRI^ESKIE OKRUVNOSTI RADIU-

SOW

1

< 1, NO OBHODIMYE W PROTIWOPOLOVNOM NAPRAWLENII:

r

1

ZNA^ENIQM z =reit

SOOTWETSTWU@T w =

e;it.

r

wYWODY MOVNO OFORMITX W WIDE SLEDU@]EGO UTWERVDE-

NIQ.

1

1

;

12

, OSU]ESTWLQET WZAIMNO-

fUNKCIQ w =

z +

,

z

C

2

z

OTOBRAVENIE:

ODNOZNA^NOE I KONFORMNOE

1

z

2 C : jzj

= 1 ,

KAK WNUTRENNOSTI OKRUVNOSTI

TAK

I EE WNE[NOSTI (WKL@^AQ

),

NA WS@ PLOSKOSTX

C c

\RAZREZOM" PO OTREZKU

[;1 1]

jzj

\

jzj < 1

\

MNOVESTW

> 1

Imz > 0

I

Imz < 0

(KAVDOE) | NA POLUPLOSKOSTX

Imw > 0 ,

A MNOVESTW

\

jzj < 1

\

jzj > 1

Imz < 0

I

Imz > 0

| NA POLU-

PLOSKOSTX

Imw < 0

oBRATNYE OTOBRAVENIQ PROIZWODQT ODNOZNA^NYe WETWI

OBRATNOJ FUNKCII z = w + pw2

;

1

(IV, c. 69).

tAK KAK PODSTANOWKA

z = eit

PREOBRAZUET SOOTNO[ENIE

w =

1

z +

1

W w = cos t, OKRUVNOSTX

z 2C : jzj= 1

FUNK-

2

z

;

1

PEREWODITSQ W DWAVDY PROHODIMYJ OTRE-

CIEJ w; =

1

z +

2

z

ZOK [

;

1

1]: SIMMETRI^NYE OTNOSITELXNO DEJSTWITELXNOJ

it

it

I z = e;

\TOJ OKRUVNOSTI PEREHODQT W

OSI TO^KI z = e

ODNU I TU VE TO^KU w 2[;1 1]. HAGLQDNYM STANOWITSQ NA-

RU[ENIE KONFORMNOSTI OTOBRAVENIQ w =

1

z+

1

W TO^KAH

z = 1.

2;

z

1 w

\NEOSOBYH" TO^KAH.

103

sREDI PRO^EGO FUNKCIQ w = 12;z + z1 WKUPE S DROBNO-LINEJNYMI

UPRO]AET IZU^ENIE OTOBRAVENIJ TRIGONOMETRI^ESKIMI (RAWNO KAK I

GIPERBOLI^ESKIMI) FUNKCIQMI.

K PRIMERU, PREDSTAWLENIE w =cos z W WIDE KOMPOZICII

iz	1	;	iz		1
z ;!7 iz ;!7 e ;!7	2			+ eiz			= cos z
		e

POZWOLQET NAGLQDNO PREDSTAWITX PREOBRAZOWANIE PRI \TOM OTOBRAVE- NII, NAPRIMER, \IZLOMANNOJ" POLOSY (RIS. 32).

rIS. 32

104

pODOBNYE PREDSTAWLENIQ OTOBRAVENIJ w = chz I w = sin z SOOT-

WETSTWENNO NA ODIN [AG KORO^E I DLINNEE:

;

z

1

;

z

1

z ;!7

e

;!7

2

e

+ ez

= ch z, a

sin z = cos

;z

2

W SLU^AE w=tgz

FUNKCI@ vUKOWSKOGO SMENQET DROBNO-LINEJNAQ:

2iz

eiz;e;iz

z

;!7

2iz

;!7

e2iz

;!7

e

2iz;1

=

2i

= tgz.

e

iz

+e;

iz

ie

+i

2

uPRAVNENIQ.

1. dOKAZATX, ^TO

a) OTOBRAVENIE w =

1

RAWNOSILXNO POSLEDOWATELXNOMU WYPOLNE-

NI@ (W L@BOM PORQDKE)

z

DWUH PREOBRAZOWANIJ SIMMETRII: OTNOSITELX-

NO EDINI^NOJ OKRUVNOSTI I DEJSTWITELXNOJ OSI

B) PREOBRAZOWANIE PODOBIQ w = z (S KO\FFICIENTOM

> 0) SWODIT-

SQ K DWUM PREOBRAZOWANIQM SIMMETRII OTNOSITELXNO OKRUVNOSTEJ S OB]IM CENTROM 0

W) POWOROT w=ei z NA UGOL (WOKRUG TO^KI 0) RAWNOSILEN DWUM PREOBRAZOWANIQM SIMMETRII OTNOSITELXNO PERESEKA@]IHSQ (W \TOJ TO^KE) PRQMYH

G) SDWIG w = z+b NA WEKTOR b RAWNOSILEN DWUM PREOBRAZOWANIQM

SIMMETRII OTNOSITELXNO PERPENDIKULQRNYH K WEKTORU b PRQMYH. nA OSNOWANII \TOGO PRIJTI K WYWODU: L@BOE DROBNO-LINEJNOE PRE-

OBRAZOWANIE RAWNOSILXNO WYPOLNENI@ ^ETNOGO ^ISLA SIMMETRIJ (OT-

NOSITELXNO PRQMYH I OKRUVNOSTEJ).

2. pROWERITX, ^TO DROBNO-LINEJNYE OTOBRAVENIQ w =

az+b

, SOOT-

cz+d

WETSTWU@]IE WRA]ENIQM SFERY rIMANA, | \TO TE, KOTORYE IME@T WID

w;w

1

=ei

z;z1

ILI

(^TO \KWIWALENTNO) HARAKTERIZU@TSQ SOOTNO-

1+z1 z

1+w1 w

c

d

a

b

[ENIQMI d =; c

=; b

= a . uKAZANIQ: A) PRI TAKIH OTOBRAVENIQH

PARY TO^EK z1 z2

c z1

= ;1,;KOTORYM PRI STEREOGRAFI^ESKOJ PRO-

z2

EKCII SOOTWETSTWU@T DIAMETRALXNO PROTIWOPOLOVNYE TO^KI SFERY

rIMANA (I, UPRAVNENIE 6), PEREHODQT W PARY TO^EK w1 w2 S TAKIM VE SWOJSTWOM B) NEPODWIVNYE TO^KI TAKIH OTOBRAVENIJ SIMMETRI^NY

OTNOSITELXNO CENTRA SFERY rIMANA I QWLQ@TSQ TO^KAMI EE PERESE^E-

NIQ S OSX@ WRA]ENIQ SFERY.

3. pRIMENQQ PODSTANOWKU z = etei ;1 < t < +1, NAJTI OBRAZY LU^EJ z 2 C : arg z = PRI OTOBRAVENII FUNKCIEJ w = 12;z+ 1z .

ANALITI^ESKOJ1 W TO^KE

105

VII. kAKIE MNOVESTWA NA PLOSKOSTI C NAZYWA@T OBLASTQMI, A FUNKCII | ANALITI^ESKIMI

fUNKCI@ KOMPLEKSNOJ PEREMENNOJ w = f(z) NAZYWA@T z 2C , ESLI ONA IMEET PROIZWODNU@ NE TOLXKO W \TOJ TO^KE, NO I W NEKOTOROJ EE OKRESTNOSTI

(W NEKOTOROM KRUGE S CENTROM W \TOJ TO^KE).

fUNKCI@, ANALITI^ESKU@ W KAVDOJ TO^KE MNOVESTWA E C , NAZYWA@T ANALITI^ESKOJ NA \TOM MNOVESTWE, A ANALITI^ESKU@ W KAVDOJ TO^KE PLOSKOSTI C | CELOJ.

tERMIN ANALITI^ESKIE FUNKCII IMEL HOVDENIE W MATEMATIKE E]E DO ZAROVDENIQ TEORII FUNKCIJ KOMPLEKSNOJ PEREMENNOJ, ODNAKO WNQT- NOGO SMYSLA ON NE IMEL. w ^ASTNOSTI, WHODQ W NAZWANIE MONOGRAFII lAGRANVA [37], ON NE WSTRE^AETSQ W EE TEKSTE.

kO[I ([28], ser. 1, t. 12, p. 35, 228) WWEL SLEDU@]U@ TERMINOLOGI@:

\fUNKCIQ DEJSTWITELXNOJ ILI MNIMOJ PEREMENNOJ z BUDET NAZYWATXSQ MONODROMNOJ, ESLI ONA NE PERESTAET BYTX NEPRERYWNOJ POKA NE OBRA- ]AETSQ W BESKONE^NOSTX ONA BUDET NAZYWATXSQ MONOGENNOJ, ESLI U NEE ESTX MONODROMNAQ PROIZWODNAQ. fUNKCIQ MOVET BYTX MONODROMNOJ I MONOGENNOJ TOLXKO DLQ ZNA^ENIJ z , SOOTWETSTWU@]IH WNUTRENNIM TO^- KAM NEKOTOROJ OBLASTI . . . sINEKTI^ESKOJ Q NAZYWA@ FUNKCI@, KOTO- RAQ DLQ WSEH KONE^NYH ZNA^ENIJ PEREMENNOJ, OT KOTOROJ ONA ZAWISIT, QWLQETSQ NE TOLXKO MONODROMNOJ I MONOGENNOJ, NO I KONE^NOJ."2

1 wARIANTY: GOLOMORFNOJ, REGULQRNOJ. gOWORQ, ^TO \ w =f(z) ESTX ANALITI^ESKAQ FUNKCIQ" PODRAZUMEWA@T, ^TO W PLOSKOSTI C ESTX TO^KI, W KOTORYH DANNAQ FUNKCIQ QWLQETSQ ANALITI^ESKOJ.

2 w ORIGINALE: \Une fonction de la variable reelle ou imaginaire z sera dite monodrome , si elle ne cesse d'^etre continue qu'en devenant in nie elle sera dite monogene, si elle a une derivee monodrome. Une fonction peut ^etre monodrome et monogene, seulement pour les valeurs de z correspondantes aux points interieurs d'une certaine aire . . . J'appelle synectique une fonction qui, pour une valeur nie de la variable dont elle depend, est toujours, non seulement monodrome et monogene, mais encorenie."

| CELYJ o ' | WID).

1 gRE^. o o&

106

pROISHOVDENIE \TIH (KAK I DRUGIH WWODIMYH IM) TERMINOW kO[I NE OB_QSNQL1, A IH TRAKTOWKA OKAZYWAETSQ NEDOSTATO^NO WNQTNOJ.

w 1875 G. WO 2-M IZDANII MONOGRAFII bRIO I bUKE [23] (S. 14) TERMIN kO[I SINEKTI^ESKAQ (FUNKCIQ) BYL WPERWYE ZAMENEN NA GO-

LOMORFNAQ2 ON I WO[EL W OBIHOD NARAWNE S TERMINOM ANALITI^ESKAQ3,

KOTORYM POLXZOWALSQ wEJER[TRASS4 [43] (Bd. I, S. 51 Bd. II, S. 77). mE- TAMORFOZA \TIH TERMINOW OTRAVENA, NAPRIMER, W KNIGE |.bORELQ [22].

nYNE MONOGENNOSTX5 PONIMA@T KAK SU]ESTWOWANIE PROIZWODNOJ5 (W TOM ILI INOM SMYSLE), A ANALITI^NOSTX5, GOLOMORFNOSTX5 I REGULQRNOSTX5 | KAK SINONIMY SU]ESTWOWANIQ PROIZWODNOJ f0(z) (W OBY^-

NOM SMYSLE) NE TOLXKO W TO^KE z0, NO I W NEKOTOROJ EE OKRESTNOSTI,

ILI, ^TO \KWIWALENTNO (II, S. 33 XII, S. 180), RAZLOVIMOSTI FUNKCII w=f(z) W RQD PO STEPENQM z;z0 W NEKOTOROM KRUGE S CENTROM z0 .

qWLQQSX ANALITI^ESKOJ W KAKOJ-LIBO TO^KE z 2C , T. E. IMEQ PROIZWODNU@ W NEKOTOROM KRUGE S CENTROM z, FUNKCIQ OKAZYWAETSQ ANALITI^ESKOJ WO WSEH TO^KAH \TOGO

KRUGA (RIS. 33, a). wYWOD: DLQ L@BOJ FUNKCII MNOVESTWO WSEH TO^EK, W KOTORYH ONA QWLQETSQ ANALITI^ESKOJ, OTKRY-

TO.

rIS. 33

| ODIN, EDINSTWENNYJ o o& | BEG, MESTO DLQ BEGA

" o& | PROISHOVDENIE, ROD " & | SWQZNYJ, NEPRERYWNYJ.

2 t. E. PODOBNAQ CELOJ (GRE^. o o&

3 pODRAZUMEWA@]IM RAZLOVIMOSTX FUNKCII W STEPENNOJ RQD.

4 Weierstrass, Karl, 1815{1897, | NEMECKIJ MATEMATIK, OSNOWATELX

(WMESTE S kO[I I rIMANOM) TEORII FUNKCIJ KOMPLEKSNOJ PEREMENNOJ.

5 fUNKCII KOMPLEKSNOJ PEREMENNOJ w=f(z) W TO^KE z0 2C .

107

tO, ^TO MNOVESTWO O C QWLQETSQ OTKRYTYM, OZNA^A- ET, ^TO WSE EGO TO^KI OKAZYWA@TSQ WNUTRENNIMI TO^KAMI \TOGO MNOVESTWA (KAVDAQ WHODIT W NEGO WMESTE S NEKOTOROJ

OKRESTNOSTX@). sIMWOLI^ESKI \TO WYRAVAETSQ FORMULOJ

8z ;z 2O =) 9 >0 8 ;j ;zj< =) 2O .1 iZ RAZBORA PRIMEROW W V NA STR. 71 SLEDUET:

a) w = z2 | CELAQ FUNKCIQ

B) SUMMA STEPENNOGO RQDA S NENULEWYM RADIUSOM SHODI-

MOSTI r QWLQETSQ ANALITI^ESKOJ FUNKCIEJ W KRUGE SHODI-

MOSTI \TOGO RQDA (a PRI r =+			1	| CELOJ).
W) FUNKCIQ w = jzj	2
		(IME@]AQ PROIZWODNU@ W EDINST-
WENNOJ TO^KE z =0) NE QWLQETSQ ANALITI^ESKOJ.
oTKRYTOE MNOVESTWO O C				NAZYWA@T	OBLASTX@	2, ESLI
DLQ L@BYH DWUH EGO TO^EK z1 z2				SU]ESTWUET SOEDINQ@]IJ

IH PUTX W O | ZADANNAQ NA NEKOTOROM OTREZKE [a b] R I

NEPRERYWNAQ NA NEM FUNKCIQ z =z(t) SO SWOJSTWAMI: z(t)2O PRI t2[a b] z(a)=z1 z(b)=z2 (RIS. 33, B).

nA SAMOM DELE SPRAWEDLIWO SLEDU@]EE UTWERVDENIE O

SOEDINIMOSTI MEVDU SOBOJ TO^EK OBLASTI.

l@BYE DWE TO^KI OBLASTI MOVNO SOEDINITX, NE WYHODQ ZA PREDELY \TOJ OBLASTI, LOMANOJ3, PRI^EM MOVNO DOPOL- NITELXNO POTREBOWATX, ^TOBY KAVDOE ZWENO \TOJ LOMANOJ BYLO PARALLELXNO ODNOJ IZ KOORDINATNYH OSEJ (RIS. 34).

1 oBOZNA^ENIE OTKRYTYH MNOVESTW O | PO NA^ALXNOJ BUKWE FR.

ouvert, ANGL. open I NEM. o en | OTKRYTYJ. pUSTOE MNOVESTWO OTKRYTO (DLQ NEGO ZNA^ENIE \TOJ FORMULY | ISTINA), NO WSE UPOMI-

NAEMYE NIVE OTKRYTYE MNOVESTWA PODRAZUMEWA@TSQ NEPUSTYMI.

2 dLQ OBOZNA^ENIQ OBLASTEJ ^A]E WSEGO ISPOLXZU@T BUKWY D I G (NA^ALXNYE ANGL. domain I NEM. Gebiet | OBLASTX).

3 sOSTOQ]EJ IZ KONE^NOGO ^ISLA POSLEDOWATELXNO SOEDINENNYH PRQ-

MOLINEJNYH OTREZKOW.

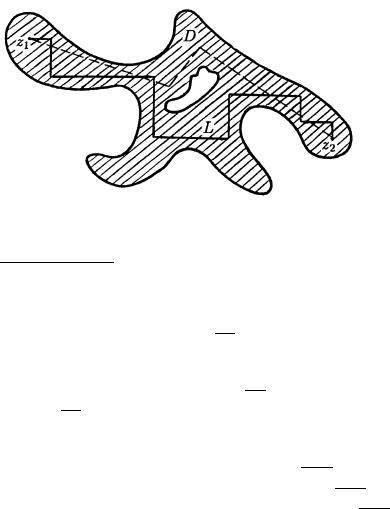
108

rIS. 34

dOKAZATELXSTWO (OT \PROTIWNOGO"). pUSTX D | OBLASTX, KAKIE-TO DWE TO^KI KOTOROGO NE SOEDINIMY (W PREDELAH \TOJ OBLASTI) LOMANOJ. nO | SOGLASNO OPREDELENI@ OBLASTI | DLQ \TIH TO^EK ESTX SOEDINQ@]IJ IH (W PREDELAH OBLASTI) PUTX z = z(t) t 2 [a b]. tO^KA z;a+2 b , SOOTWETSTWU@]AQ SEREDINE OTREZKA [a b], OKAZYWAETSQ LIBO SOEDINIMOJ, LIBO NE SOEDINIMOJ S TO^KOJ z(a) LOMANOJ W PERWOM SLU^AE W

KA^ESTWE [a1 b1] WYBIRA@T OTREZOK [a+2 b b], A WO WTOROM |

OTREZOK [a a+2 b ]. tAK ILI INA^E PUTX z = z(t) t 2 [a1 b1], SOEDINQET TO^KI, NE SOEDINIMYE (W PREDELAH OBLASTI D) LO-

MANOJ. s OTREZKOM [a1 b1] POSTUPA@T TAK VE: W SLU^AE SOEDINIMOSTI (W PREDELAH OBLASTI D) TO^KI z(a1+2 b1) S TO^KOJ z(a1) LOMANOJ W KA^ESTWE [a2 b2] BERUT OTREZOK [a1+2 b1 b], W SLU^AE VE IH NESOEDINIMOSTI POLAGA@T [a2 b2] = [a a1+2 b1 ]. pOSLEDOWATELXNOE WYPOLNENIE \TOJ PROCEDURY PRIWODIT K STQGIWA@]EJSQ POSLEDOWATELXNOSTI WLOVENNYH OTREZKOW

[a b] [a1 b1] [a2 b2] [an bn] ,

IME@]IH OB]U@ TO^KU . tAK KAK OBLASTX D | OTKRYTOE MNOVESTWO, TO^KA z( ) PRINADLEVIT OBLASTI D WMES- TE S NEKOTORYM KRUGOM S CENTROM z( ), A ESLI U^ESTX, ^TO

z0 zn+1.

t2[0 n+1],

z0 zn+1 , TO

109

fz(an)g!z( ) I fz(bn)g!z( ) (WWIDU NEPRERYWNOSTI FUNK-

CII z = z(t) NA OTREZKE [a b]), TO SLEDUET WYWOD: OBE TO^KI z(an) z(bn) POPADA@T (PRI DOSTATO^NO BOLX[OM n) W UKA- ZANNYJ KRUG, PRI^EM | PO POSTROENI@ | \TI TO^KI NE SOEDINIMY (W PREDELAH OBLASTI D) LOMANOJ. nO \TO PROTI- WORE^IT \LEMENTARNOMU GEOMETRI^ESKOMU FAKTU: W PREDELAH KRUGA L@BYE DWE EGO TO^KI SOEDINIMY MEVDU SOBOJ LOMANOJ (SO ZWENXQMI, PARALLELXNYMI OSQM KOORDINAT). Q.E.D.

zAME^ANIE. sOEDINIMOSTX TO^EK POSREDSTWOM LOMANOJ

ESTX BOLEE SILXNOE TREBOWANIE, NEVELI IH SOEDINIMOSTX PO-

SREDSTWOM PUTI: ESLI z0 z1 z2 : : : zn zn+1 | POSLEDOWA- TELXNYE WER[INY LOMANOJ, SOEDINQ@]EJ TO^KI

8z + t(z ;z ) PRI 06t61

> 0 1 0

z = <z1 + (t;1)(z2 ; z1) PRI 16t62

: : : : : : : : : : : : : : : : : : : : : : : : :>zn+ (t;n)(zn+1 ;zn) PRI n6t6n+1

ESTX PUTX (OSU]ESTWLQ@]IJ OBHOD \TOJ LOMANOJ), KOTORYJ

SOEDINQET TO^KI

w MATEMATIKE RAZLI^A@T PONQTIQ SWQZNOGO I LINEJNOGO SWQZNOGO MNOVESTWA1.

mNOVESTWO E NAZYWA@T SWQZNYM, ESLI PRI L@BOM EGO RAZDELE-

NII NA DWA (NEPUSTYH I NEPERESEKA@]IHSQ) PODMNOVESTWA E0 E1 PO KRAJNEJ MERE ODNO IZ NIH SODERVIT (HOTQ BY ODNU) PREDELXNU@ TO^KU DRUGOGO.2

mNOVESTWO E NAZYWA@T LINEJNO SWQZNYM, ESLI DLQ L@BYH DWUH EGO TO^EK z0 z1 SU]ESTWUET SOEDINQ@]IJ IH PUTX z = z(t) t 2 [a b], PROHODQ]IJ PO MNOVESTWU E.

1 zDESX RE^X IDET O MNOVESTWAH NA PLOSKOSTI C , NO \TI PONQTIQ PRIMENIMY K MNOVESTWAM W KOORDINATNYH PROSTRANSTWAH Rn L@BOJ RAZMERNOSTI (I W BOLEE OB]IH PROSTRANSTWAH).

2 |KWIWALENTNO: NE SU]ESTWUET DWUH NEPERESEKA@]IHSQ OTKRYTYH MNOVESTW O0 O1 , OB_EDINENIE KOTORYH SODERVIT WSE MNOVESTWO E , A KAVDOE IZ NIH OTDELXNO | ^ASTX \TOGO MNOVESTWA.

dLQ OTKRYTYH

110

l@BOE LINEJNO SWQZNOE MNOVESTWO QWLQETSQ SWQZNYM1 OBRATNOE VE UTWERVDENIE (DLQ MNOVESTW, NE QWLQ@]IHSQ OTKRYTYMI) NEWERNO (UPRAVNENIE 3).

MNOVESTW O C PONQTIQ SWQZNOSTI, LINEJNOJ SWQZNOSTI I SWQZNOSTI POSREDSTWOM LOMANYH SOWPADA@T. dLQ PRO-

WERKI \TOGO (S U^ETOM DOKAZANNOGO WY[E) DOSTATO^NO USTANOWITX, ^TO L@BYE DWE TO^KI SWQZNOGO OTKRYTOGO MNOVESTWA O MOVNO SOEDINITX LOMANOJ, NE WYHODQ]EJ ZA PREDELY \TOGO MNOVESTWA. eSLI BY \TO BYLO

NE TAK, T. E. ESLI BY DLQ KAKIH-TO DWUH TO^EK z0 z1		2O TAKOJ LOMANOJ
NE SU]ESTWOWALO, TO MNOVESTWO O OKAZYWALOSX BY OB_EDINENIEM DWUH
NEPERESEKA@]IHSQ OTKRYTYH MNOVESTW
	def	W Og,
O0	= fz 2O : z SOEDINIMA S z0 LOMANOJ
	def
O1	= fz 2O : z NE SOEDINIMA S z0 LOMANOJ W Og,

NI ODNA TO^KA KAVDOGO IZ KOTORYH NE QWLQETSQ PREDELXNOJ DLQ DRUGOGO.

l@BOE OTKRYTOE MNOVESTWO O C QWLQETSQ LIBO OB-

LASTX@, LIBO OB_EDINENIEM KONE^NOGO ILI BESKONE^NOGO2

^ISLA NEPERESEKA@]IHSQ OBLASTEJ3.

dLQ DOKAZATELXSTWA DOSTATO^NO RAZDELITX MNOVESTWO O NA POD- MNOVESTWA, OTNOSQ TO^KI z1 z2 2O K ODNOMU PODMNOVESTWU, ESLI \TI TO^KI SOEDINIMY W MNOVESTWE O LOMANOJ. pOLU^ENNYE MNOVESTWA OKA-

ZYWA@TSQ OTKRYTYMI, LINEJNO SWQZNYMI, I NEPERESEKA@]IMISQ.

1

dOKAZATELXSTWO

pUSTX

E = E0 [E1

| L@BOE RAZDELENIE LINEJ-

.

NO SWQZNOGO MNOVESTWA E NA DWA (NEPERESEKA@]IHSQ) PODMNOVESTWA

I z = z(t) t

2 [a b] | PROHODQ]IJ PO MNOVESTWU E

PUTX, SOEDINQ@-

]IJ KAKIE-TO TO^KI z0

E0

I z1

E1

. w KA^ESTWE [a1 b1]

WYBIRAETSQ

a+b

2a+b

2

a+b

a+b

OTREZOK [

2

b], ESLI

z

2

2E0, I OTREZOK [a

2

], ESLI z

2

2E1 W

TOM I DRUGOM SLU^AE z;(a1) 2 E0 z(b1)

2 E1. pOSLEDOWATELXNOE;

PRODOL-

VENIE \TOGO PROCESSA PRIWODIT K STQGIWA@]EJSQ POSLEDOWATELXNOSTI

WLOVENNYH OTREZKOW

[a b]

[a1 b1]

[a2 b2] [an bn]

SO SWOJSTWOM: z(an) 2 E0

z(bn) 2 E1

n = 1 2 : : :

eSLI | OB]AQ

TO^KA \TIH OTREZKOW

, TO z( ) QWLQETSQ PREDELXNOJ TO^KOJ DLQ OBO-

IH MNOVESTW E0 E1

(WNE ZAWISIMOSTI OT TOGO, KOTOROMU IZ NIH ONA

PRINADLEVIT). Q.E.D.

2 tO^NEE, S^ETNOGO.

3 |TO VE OTNOSITSQ K OTKRYTYM MNOVESTWAM O Rn .