Шведенко Начала анализа функций комплексной переменной 2008

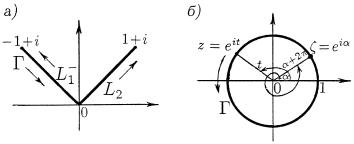
131

R

f(z)dz =

R

f(z)dz +

R

f(z)dz =;

R

f(z)dz+

R

f(z)dz,

;

L1

L2

L;

L2

1

A TAK KAK W KA^ESTWE PUTEJ OBHODA (KLASSA C1) ORIENTIRO-

L1

L2

WANNYH OTREZKOW

;

MOVNO WZQTX SOOTWETSTWENNO FUNK-

CII z =(;1+i)t1

t2[0 1],

I z =(1+i)t1

t2[0 1], TO

R

f(z)dz =;0

f((;1+i)t)(;1+i)dt +

0

f((1+i)t)(1+i)dt

;

R

R

W ^ASTNOSTI,

R

R

R

1

1

;

z

dz =

;0

(;1+i)t(;1+i)dt +

0

(1+i)t(1+i)dt = 0.

rIS. 45

2. pUSTX ; | OKRUVNOSTX RADIUSA 1 S CENTROM 0, OD-

NOKRATNO OBHODIMAQ OT EE TO^KI = ei W POLOVITELXNOM

NAPRAWLENII (\PROTIW HODA ^ASOWOJ STRELKI"). tAK KAK ZA

PUTX OBHODA (KLASSA C1) \TOGO ZAMKNUTOGO GLADKOGO KONTU-

RA MOVNO WZQTX FUNKCI@ z = eit t 2 [ +2 ] (RIS. 45, B), DLQ L@BOJ NEPRERYWNOJ NA ; FUNKCII w =f(z)

		+2		2
	f(z)dz =		f(eit)ieitdt =		f(eit)ieitdt
;				0
		R		R
H						2 -PERIODI^NOSTI
POSLEDNEE RAWENSTWO (A ONO WYTEKAET IZ

PODYNTEGRALXNOJ FUNKCII) ILL@STRIRUET NEZAWISIMOSTX

132

INTEGRALA PO ZAMKNUTOMU KONTURU ; OT WYBORA EGO NA^ALX-

NOJ TO^KI1 (SLUVA]U@ OPRAWDANIEM ZAPISI

jzj = 1 W KA-

^ESTWE SIMWOLA KONTURA) W ^ASTNOSTI,

2

Rezdz =

cos t(cos t+i sin t)idt = i .

zH=1

0

3.

j j

; | TOTRVE ZAMKNUTYJ GLADKIJ KONTUR, ^TO

pUSTX

I W PRIMERE 2 (S TOJ VE NA^ALXNOJ TO^KOJ =ei I TEM VE

PUTEM z = eit

2

i

t

[ +2 ] EGO OBHODA. eSLI SREDI MNOVES-

TWA WSEH ZNA^ENIJ Ln = Lne

WYBRANO i , TO PRI L@BOM

WYBORE ^ISLA

2

( +2 ), OTWE^A@]EM RAZDELENI@ KON-

i

DO TO^KI

e

i

) I ;2 (OT

TURA ; NA U^ASTKI ;1

(OT TO^KI e

TO^KI ei

DO TO^KI ei( +2 )),

H

R

R

+2

Lnzdz =

ln zdz +

t= +2

R

+

R

ln zdz =

(0+it)(eit)0dt =

;

R

;1

;2

2

R

+2

+2

=

it(eit)0dt = iteit

;

ieitdt = 2 iei = 2 i

H

t=

ZNA^ENIE

Lnzdz

OKAZYWAETSQ

ZAWISQ]IM OT TOGO, KAKAQ

;

TO^KA ZAMKNUTOGO KONTURA ; WZQTA W KA^ESTWE NA^ALXNOJ.

pOQSNENIE. wDOLX U^ASTKOW ;1 I ;2 INTEGRIRU@TSQ DWE RAZNYE WETWI LOGARIFMA, KOTORYE PRODOLVA@T DRUG DRUGA W TO^KE ei , NO

NE SOWPADA@T W TO^KE = ei = ei( +2 ): DLQ PERWOJ IZ NIH	ln =i,
TOGDA KAK DLQ WTOROJ ln =i( +2 . zAWISIMOSTX ZNA^ENIQ	Lnzdz OT

WYBORA NA^ALXNOJ TO^KI ZAMKNUTOGO KONTURA ; OB_QSNQETSQ TEM,

H;

^TO PRI ZAMENE EE DRUGOJ, 0 = ei0 ( < 0 < +2 ), NA SOEDINQ@]EJ

^

IH DUGE 0 ZNA^ENIQ PODYNTEGRALXNOJ FUNKCII BERUTSQ UVE S DRUGOJ EE WETWI | TOJ, DLQ KOTOROJ NA \TOJ DUGE ln z =it S +2 6t6 0+2

(A NE 6t6 0).

1 s. 128, SWOJSTWO 4, B.

2 kAK O TOM GOWORILOSX W ZAME^ANII 1 (S. 130).

DEJ-

133

oCENKA INTEGRALA PO KONTURU. eSLI jf(z)j 6 h NA

KUSO^NO-GLADKOM KONTURE ; (DLINY l(;)1), TO

Rf(z)dz 6h l(;).

;

dOKAZATELXSTWO. w SILU SWOJSTWA ADDITIWNOSTI (S. 128)

DOSTATO^NO RASSMOTRETX SLU^AJ, KOGDA KONTUR ; SOSTOIT IZ ODNOJ (ORIENTIROWANNOJ) GLADKOJ DUGI L. tAK KAK FUNKCIQ

2

1

z = z(t),

t

[a b], ZADA@]AQ PARAMETRIZACI@ (S. 117) \TOJ

GLADKOJ DUGI, ODNOWREMENNO SLUVIT PUTEM (KLASSA C ) OB-

HODA LIBO SAMOGO KONTURA ;, LIBO PROTIWOPOLOVNO ORIEN-

TIROWANNOGO KONTURA ;;,2

R

R

R

6 b

b

b

;

f(z)dz =

a f(z(t))z(t)dt 6 a jf(z(t))jjz(t)jdt 6

R

3

a hjz(t)jdt = h l(L)

(S. 117). Q.E.D.

fORMULA nX@TONA

{ lEJBNICA. eSLI KUSO^NO-GLAD-

4

KIJ KONTUR ; RASPOLOVEN W OBLASTI D

C , W KOTOROJ FUNK-

CIQ w = f(z) NEPRERYWNA I IMEET PERWOOBRAZNU@ '(z), TO

Rf(z)dz = '(z );'(z ),

;

GDE z I z | SOOTWETSTWENNO NA^ALXNAQ I KONE^NAQ TO^KI KONTURA ; W ^ASTNOSTI, ESLI \TOT KONTUR ZAMKNUT, TO

Hf(z)dz =0.

;

1 pONIMAEMOJ KAK SUMMA DLIN SOSTAWLQ@]IH KONTUR ; GLADKIH DUG. 2 ~TO ZAWISIT OT TOGO, KAK ORIENTIROWANA GLADKAQ DUGA L: KAKAQ

IZ DWUH EE KONCEWYH TO^EK z(a) z(b) QWLQETSQ NA^ALXNOJ.

3 aNGLIJSKIJ MATEMATIK I FIZIK nX@TON (Newton, Isaac, 1643 { 1727) I NEMECKIJ MATEMATIK I FILOSOF lEJBNIC (PRAWILXNEE lQJBNIC,

Leibniz, Gottfried Wilhelm, 1646 {1716) OPERIROWALI EJ (W SLU^AE

STWITELXNOJ PEREMENNOJ) E]E DO OFORMLENIQ PONQTIQ INTEGRALA. 4 t. E. f(z)='0(z) W OBLASTI D.

134

dOKAZATELXSTWO. pUSTX z = z(t) t 2 [a b], | L@BOJ PUTX

(KLASSA C1) OBHODA KONTURA ; (S. 125). sOGLASNO OPREDELE-

NI@ KONTURNOGO INTEGRALA (S. 127) I KLASSI^ESKOJ FORMU-

LE nX@TONA{lEJBNICA (DLQ INTEGRALA PO OTREZKU FUNKCII

DEJSTWITELXNOJ PEREMENNOJ)

				def b		b		d
		f(z)dz = '0		(z)dz = '0((z(t))z(t)dt =					'(z(t))dt =
;		;		a		a		dt
						R
R		R = '(z(b))R			'(z(a)) = '(z )		'(z ). Q.E.D.
	zAME^ANIE			;	;
			. pRAWU@ ^ASTX FORMULY nX@TONA{lEJBNICA

(RAZNOSTX ZNA^ENIJ PERWOOBRAZNOJ PODYNTEGRALXNOJ FUNK- CII W KONE^NOJ I NA^ALXNOJ TO^KAH KONTURA) MOVNO TRAK-

TOWATX KAK PRIRA]ENIE PERWOOBRAZNOJ WDOLX KONTURA ; S ZAPISX@ FORMULY W WIDE Rf(z)dz = M' ;.

;

uPRAVNENIQ. 1. pROWERITX, ^TO WZAIMNO ODNOZNA^NYJ OBRAZ L OT- REZKA [;1 1] PRI OTOBRAVENII FUNKCIEJ z =t2+it3 NE QWLQETSQ GLADKOJ DUGOJ, HOTQ W KAVDOJ TO^KE z 2 L SU]ESTWUET KASATELXNAQ PRQMAQ K L, POLOVENIE KOTOROJ NEPRERYWNO ZAWISIT OT TO^KI KASANIQ.

2. dOKAZATX, ^TO L@BAQ GLADKAQ DUGA L C ESTX LIBO GRAFIK FUNKCII WIDA y =y(x) a6x6b, ILI x=x(y) c6y 6d, LIBO REZULXTAT GLADKOGO SOEDINENIQ NESKOLXKIH TAKIH GRAFIKOW. (wOSPOLXZOWATXSQ TEM, ^TO ESLI FUNKCIQ z = z(t) = x(t)+iy(t) t 2 [a b], ZADAET PARAMETRIZACI@ GLADKOJ DUGI L, TO OTREZOK [a b] DOPUSKAET RAZBIENIE NA KONE^NOE ^ISLO OTREZKOW, NA KAVDOM IZ KOTORYH HOTQ BY ODNA IZ PROIZWODNYH

x0(t) y0(t) SOHRANQET ZNAK .)

3. dOKAZATX, ^TO OKRUVNOSTX NE QWLQETSQ GLADKOJ DUGOJ. (pRIJTI K PROTIWORE^I@, PREDPOLOVIW, ^TO NEPRERYWNAQ NA OTREZKE FUNKCIQ z =z(t) WZAIMNO-ODNOZNA^NO OTOBRAVAET EGO NA OKRUVNOSTX.)

4.

pOSTROITX PUTX KLASSA C1, OBHODQ]IJ DWUHZWENNU@ LOMANU@,

IZOBRAVENNU@ NA RIS. 45, A.

5.

wYQSNITX, L@BOJ LI PUTX KLASSA C1 QWLQETSQ PUTEM OBHODA

NEKOTOROGO KUSO^NO-GLADKOGO KONTURA. (oTWET: NET.)

dOKAZATX, ^TO ESLI Rez 6 0, TO

z

z

zn

n+1

6.

e

;1; 1!

; ; n!

6 jzj

.

(pRIMENITX INDUKCI@ PO n.)

135

IX. ~TO NAZYWA@T INDEKSOM ZAMKNUTOGO KONTURA I NA ^TO ON UKAZYWAET

wAVNYM DLQ DALXNEJ[EGO PRIMEROM PRIMENENIQ FOR-

MULY nX@TONA{lEJBNICA (VIII, S. 133) SLUVIT WY^ISLENIE

ZNA^ENIQ

1

dz

, GDE

; | ZAMKNUTYJ KUSO^NO-GLADKIJ

2 i

;

z;z0

H

, NE PROHODQ]IJ ^EREZ TO^KU z0

2C .

KONTUR ; NA PLOSKOSTI C

pRQMOE PRIMENENIE FORMULY nX@TONA{lEJBNICA ZDESX

ZATRUDNENO TEM, ^TO PERWOOBRAZNYMI DLQ PODYNTEGRALXNOJ

FUNKCII SLUVAT ODNOZNA^NYE WETWI

w = ln(z ;z0) MNOGO-

ZNA^NOJ FUNKCII

w = Ln(z ;z0) (V ,

S

. 78),

A WYDELITX KA

-

KU@-LIBO IZ NIH W OBLASTI, CELIKOM SODERVA]EJ KONTUR ;, MOVNO LI[X DLQ OTDELXNYH WIDOW KONTUROW1.

w PODOBNYH SLU^AQH (KOGDA PODYNTEGRALXNAQ FUNKCIQ W Rf(z)dz IMEET \MNOGOZNA^NU@ PERWOOBRAZNU@" w = (z))

;

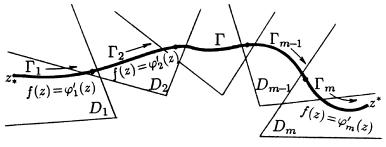
WYHOD SOSTOIT W RAZDELENII KONTURA ; NA U^ASTKI (KUSO^NO-

GLADKIE KONTURY ;1 : : : ;m), CELIKOM RASPOLOVENNYE W OBLASTQH (D1 : : : Dm), W KOTORYH MOVNO WYDELITX ODNOZNA^-

NYE WETWI (w='1(z) : : : w ='m(z)) MNOGOZNA^NOJ FUNKCII w = (z) (RIS. 46). pOSLE \TOGO OSTAETSQ PRIMENITX FOR-

MULU nX@TONA{lEJBNICA K KAVDOMU U^ASTKU ;1 : : : ;m I

WOSPOLXZOWATXSQ SWOJSTWOM ADDITIWNOSTI (VIII, S. 128):

Rf(z)dz =M'1 ;1 + + M'm ;m .

iZ SAMOGO;\TOGO RAWENSTWA SLEDUET, ^TO EGO PRAWAQ ^ASTX NE ZAWISIT OT KONKRETNOGO RAZDELENIQ KONTURA ; NA U^AS-

TKI ;1 : : : ;m, RAWNO KAK OT WYBORA ODNOZNA^NYH WETWEJ w = '1(z) : : : w = 'm(z). eSLI VE \TI WETWI NEPRERYWNO

1 nAPRIMER, NE PERESEKA@]IH NEKOTORYJ LU^, WYHODQ]IJ IZ TO^KI z0 (IV, S. 68).

136

PRODOLVA@T DRUG DRUGA (SOWPADA@T W TO^KAH SOEDINENIQ

U^ASTKOW ;1 S ;2 : : : ;m;1 S ;m), TO

M'1 ;1 + + M'm ;m ='m(z );'1(z ),

(z | KONE^NAQ, A z | NA^ALXNAQ TO^KI KONTURA ;)1, ^TO POZWOLQET PRIDATX FORMULE nX@TONA{lEJBNICA WID

Rf(z)dz =M ; ,

;

ESLI PRAWU@ ^ASTX PONIMATX IMENNO KAK 'm(z );'1(z ) | SUMMARNOE PRIRA]ENIE PRODOLVA@]IH DRUG DRUGA WETWEJ \MNOGOZNA^NOJ PERWOOBRAZNOJ" WDOLX KONTURA ;.

rIS. 46

wOZMOVNOSTX UPOMQNUTOGO RAZDELENIQ KONTURA | PRI USLOWII, ^TO ON NE PROHODIT ^EREZ TO^KI WETWLENIQ (IV , S. 62) \MNOGOZNA^NOJ PER-

WOOBRAZNOJ" w = (z) PODYNTEGRALXNOJ FUNKCII W f(z)dz, | MOVNO

									;
DOKAZATX, RASSUVDAQ \OT PROTIWNOGO".									R
pUSTX : z = z(t) t 2		[a b], | PUTX (KLASSA C1) OBHODA KONTURA
; (VIII, S. 125), I PUSTX OTREZOK [a b]							NELXZQ RAZDELITX NA KONE^NOE
^ISLO OTREZKOW	[a t1] : : : [tm;1 b]					S TEM		,	^TOBY SOOTWETSTWU@]IE IM
1 pRI \TOM W SLU^AE z		= z			(ZAMKNUTOGO KONTURA) NE OBQZATELXNO
'm(z )='1 (z ).

137

U^ASTKI KONTURA ; | MEVDU TO^KAMI z(a) I z(t1) : : : z(tm;1) I z(b) | OKAZYWALISX W OBLASTQH, GDE OPREDELENY ODNOZNA^NYE WETWI w = '(z)

MNOGOZNA^NOJ FUNKCII w = (z).

rAZDELIW OTREZOK [a b] POPOLAM, MOVNO UTWERVDATX, ^TO PO KRAJ-

NEJ MERE ODIN IZ OTREZKOW [a a+b ] [a+b ,b] (OBOZNA^AEMYJ DALEE [a1 b1])

2 2

OBLADAET TEM VE SWOJSTWOM: EGO NELXZQ RAZDELITX NA KONE^NOE ^ISLO OTREZKOW S TEM, ^TOBY SOOTWETSTWU@]IE IM U^ASTKI KONTURA ; OKAZY- WALISX W OBLASTQH, GDE OPREDELENY ODNOZNA^NYE WETWI MNOGOZNA^NOJ FUNKCII w= (z).

pRODOLVENIE \TOGO PROCESSA PRIWODIT K STQGIWA@]EJSQ POSLEDO-

WATELXNOSTI WLOVENNYH OTREZKOW [a b]		[a1 b1]		[an bn]		,
				^
KAVDYJ IZ KOTORYH OBLADAET UKAZANNYM SWOJSTWOM. pUSTX t | OB]AQ

TO^KA \TIH OTREZKOW I			^
			z(t) | SOOTWETSTWU@]AQ EJ TO^KA KONTURA ;.
tAK KAK	^	NE QWLQETSQ TO^KOJ WETWLENIQ MNOGOZNA^NOJ FUNKCII
	z(t)

w = (z), W NEKOTOROM KRUGE S CENTROM	^	OPREDELENA EE ODNOZNA^NAQ
	z(t)
WETWX w='(z).

zDESX I ZAKL@^ENO PROTIWORE^IE: S ODNOJ STORONY, KAKOWO BY NI BYLO n, U^ASTOK KONTURA ;, SOOTWETSTWU@]IJ (PRI EGO OBHODE z =z(t), t 2 [a b]) ZNA^ENIQM t OT an DO bn, PO POSTROENI@ NE MOVET CELIKOM RASPOLAGATXSQ W OBLASTI, GDE OPREDELENA ODNOZNA^NAQ WETWX w ='(z)

S DRUGOJ STORONY OTREZKI n n STQGIWA@TSQ K TO^KE ^ A POTOMU

, [a b ] t,

SOOTWETSTWU@]IE IM U^ASTKI KONTURA ; (OTWE^A@]IE IZMENENI@ t OT

an DO bn) PRI DOSTATO^NO BOLX[IH ZNA^ENIQH n CELIKOM OKAZYWA@T-

^

TAKAQ

SQ W UPOMQNUTOM KRUGE (S CENTROM z(t)), W KOTOROM OPREDELENA

ODNOZNA^NAQ WETWX.

w RASSMATRIWAEMOM KONKRETNOM SLU^AE

1

H

dz

1

1

;

2 i ; z;z0

=

2 iMLn(z;z0) ;

= 2 iM lnjz;z0j+iArg(z;z0)

; =

=

1

MArg(z;z0) ;

1.

2

pOSLEDNEE WYRAVENIE | DELENNOE NA 2 SUMMARNOE PRI-

RA]ENIE PRODOLVA@]IH DRUG DRUGA ODNOZNA^NYH WETWEJ

'=arg(z;z0) | ESTX NI^TO INOE KAK SUMMARNOE ^ISLO OBO-

1 Mlnjz;z0j ; =lnjz ;z0j ;lnjz ;z0j

=0, TAK KAK KONTUR ; ZAMKNUT

(z = z ), A FUNKCIQ w =ln z

;

z0

ODNOZNA^NA.

j

j

LENII.3

W PROTIWOPOLOVNOM NAPRAW-

138

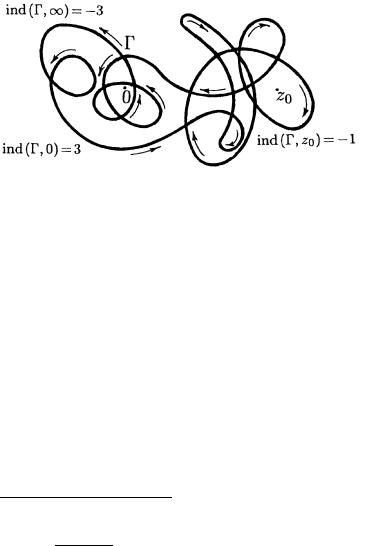
ROTOW1 WEKTORA z;z0 (WOKRUG TO^KI z0) PRI OBHODE TO^KI z WDOLX ZAMKNUTOGO KONTURA ;. |TO ^ISLO (A ONO ZAWEDOMO QW-

LQETSQ CELYM) NAZYWA@T INDEKSOM (ZAMKNUTOGO) KONTURA ; OTNOSITELXNO TO^KI z0 2:

	def	1		H	dz
	ind(; z0) = 2 i				z;z0		.
				;

zAPISX ind(; z0)= n QWLQETSQ, TAKIM OBRAZOM, FORMULXNYM WYRAVENIEM NAGLQDNOGO PREDSTAWLENIQ O TOM, ^TO ZA-

MKNUTYJ KONTUR ; OBHODIT TO^KU z0 (W OB]EJ SLOVNOS-

TI) n RAZ W POLOVITELXNOM NAPRAWLENII (SOOTWETSTWENNO

j		j	def
	n		RAZ W OTRICATELXNOM, ESLI	n < 0 RIS. 47). pOLAGA@T

TAKVE ind(; 1) = ;ind(; 0): OBHOD TO^KI 0 ODNOWREMENNO S^ITAETSQ OBHODOM TO^KI 1

rIS. 47

1 oBOROTY \PROTIW HODA ^ASOWOJ STRELKI" S^ITA@TSQ SO ZNAKOM \PL@S", A W PROTIWOPOLOVNOM NAPRAWLENII | SO ZNAKOM \MINUS".

2 iLI INDEKSOM TO^KI z0 OTNOSITELXNO KONTURA ;.

3 pRI^INY \TOGO WIDNY IZ RASSMOTRENIQ SFERY rIMANA (I, S. 21).

139

nAGLQDNO PONQTIE INDEKSA

(OTNOSITELXNO TO^KI

z0 2 C ) MOVNO

OPREDELITX DLQ L@BOGO (NE PROHODQ]EGO ^EREZ \TU TO^KU) ZAMKNUTOGO

PUTI : z = z(t) t

2

[a b]1. a IMENNO, ind( z0)

POLAGAETSQ RAWNYM

^ISLU OBOROTOW

2

WEKTORA z(t) z0 PRI WOZRASTANII t OT a DO b, PRI^EM

W SLU^AE PUTI

KLASSA C

1

;

WYPOLNQETSQ RAWENSTWO

1

dz

def

1

b

z(t)dt

3

ind( z0)=

2 i

z;z0

=

2 i a z(t);z0

.

R

ZAMKNUTOGO KONTURA

w SOOTWETSTWII S \TIM OPREDELENIEM INDEKS

H

;

; (OTNOSITELXNO KAKOJ-LIBO TO^KI z0) SOWPADAET S INDEKSOM L@BOGO PUTI , OSU]ESTWLQ@]EGO OBHOD \TOGO KONTURA.

pONQTIE INDEKSA ZAMKNUTOGO KONTURA (HOTQ I W DRUGIH TERMINAH I OBOZNA^ENIQH) WWEL kO[I [28] (ser. I, t. 12, p. 222{224 ser. II, t. VI,

	p. 121). w SOOTWETSTWII S EGO PODHODOM ind(; z0) | \TO WZQTOE S KO\F-
	FICIENTOM		1	^ISLO PEREMEN ZNAKA4 WELI^INY	Re (z;z0) W TO^KAH OBRA-
		2
					Im (z;z0)
	]ENIQ EE W	BESKONE^NOSTX PRI PEREME]ENII z			WDOLX KONTURA ;.

oPERIRUQ INDEKSOM (I FORMULOJ nX@TONA{lEJBNICA),

UDOBNO WY^ISLQTX INTEGRALY RACIONALXNYH FUNKCIJ | OT-

NO[ENIJ pq((zz)) MNOGO^LENOW | PO NE PROHODQ]IM ^EREZ \OSO-

BYE TO^KI" \TIH FUNKCIJ (KORNI ZNAMENATELEJ) ZAMKNUTYM KUSO^NO-GLADKIM KONTURAM. dOSTATO^NO WOSPOLXZOWATXSQ RAZ- LOVIMOSTX@ L@BOJ RACIONALXNOJ FUNKCII W SUMMU MNOGO-

^LENA I PROSTYH DROBEJ:

p(z) q(z)

A1

Ak

B1

Bm

= p0(z) + z;a + + (z;a)k + z;b + + (z;b)m +

C1

Ck

+ z;c + + (z;c)n

1 zAMKNUTOSTX PUTI OZNA^AET SOWPADENIE EGO NA^ALXNOJ I KO-

NE^NOJ TO^EK: z(b)=z(a).

2 pRI POLOVITELXNOM IH OTS^ETE \PROTIW HODA ^ASOWOJ STRELKI". 3 eSLI NE QWLQETSQ PUTEM KLASSA C1 , TO \TOT INTEGRAL MOVET

POTERQTX SMYSL.

4 s SOGLA[ENIEM S^ITATX KAVDU@ PEREMENU ZNAKA S \MINUSA" NA \PL@S" ZA 1, A S \PL@SA" NA \MINUS" | ZA ;1.

140

ZDESX a b : : : c | KORNI MNOGO^LENA q(z)					(ZNAMENATELQ),
k m : : : n | KRATNOSTI \TIH KORNEJ, A					A1 : : : Cn					|
KOMPLEKSNYE ^ISLA1 (O ^EM NIVE W XIV , c. 225{227).
tAK KAK, ISKL@^AQ LI[X DROBI	A1	,	B1		, : : : ,			C1	,	WSE
			z;b
2	z;a					f		z;c		g
SLAGAEMYE RAZLOVENIQ IME@T W OBLASTI C r							a b : : : c

PERWOOBRAZNYE , PRIMENENIE FORMULY nX@TONA{lEJBNICA (VIII, c. 133) DAET: DLQ L@BOGO NE PROHODQ]EGO ^EREZ TO^KI

a b : : : c ZAMKNUTOGO KUSO^NO-GLADKOGO KONTURA ; C

H

p(z)

H

A1

H

B1

H

C1

q(z) dz =

z;a dz +

z;b dz + +

z;c dz =

;

;

;

;

;

= 2 i A1 ind(; a)+B1 ind(; b)+ +C1 ind(; c) .

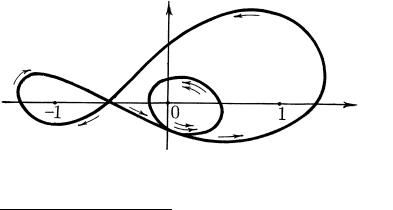
nAPRIMER, DLQ ZAMKNUTOGO KUSO^NO-GLADKOGO KONTURA ;,

IZOBRAVENNOGO NA RIS. 48, INDEKSY KOTOROGO OTNOSITELXNO

TO^EK ;1 1 0 RAWNY SOOTWETSTWENNO

;1 1 3,

H

dz

H;

1

1

1

;

1

1

z(z2;1)

=

2(z;1)

+ 2(z+1) ; z

+ 2 ; 3

.

;

;

dz = 2 i ; 2

rIS. 48

1 oBY^NO NAHODIMYE METODOM NEOPREDELENNYH KO\FFICIENTOW.

2		A2		A2
	k PRIMERU,	(z;a)2	= ;;z;a 0.