
- •1 Стратегия развития отечественной энергетики.
- •2 Выбор числа и мощности трансформаторов на подстанции. Нагрузочная способность.
- •3 Системы отопления, вентиляции, горячего водоснабжения и пароснабжения предприятий. Их назначение. Режимы работы. Требуемые параметры тепла.
- •2.5. Паровые системы теплоснабжения
- •4 Выбор электрических аппаратов, изоляторов, электрических проводов по условиям рабочего (нормального) режима.
- •5 Энергетические обследования и энергоаудит объектов теплоэнергетики и теплотехнологий: задачи, виды, нормативная база.
- •5 Нормативно-правовая и нормативно-техническая база энергосбережения.
- •6 Суточные и сменные графики теплопотребления. Методика определения максимальных, средних и годовых потребностей в теплоте каждым типом потребителей.
- •7 Теплопроводность через плоские, цилиндрические, 1-слойные и многослойные стенки.
- •7 Теплопередача через плоские и цилиндрические стенки. Термическое сопротивление теплопередачи через плоские и цилиндрические стенки. Коэффициент теплопередачи; интенсификация теплопередачи.
- •Цилиндр стенки
- •8 Методы определения потребностей промышленных предприятий в теплоте пара и горячей воды
- •8 Методы регулирования отпуска теплоты из систем централизованного теплоснабжения.
- •9Защита линий электрических сетей от токов коротких замыканий.
- •10 Сушильные установки: назначение, устройство и принцип работы.
- •11 Защита от атмосферного электричества сельскохозяйственных предприятий.
- •12 Теплообменные аппараты: назначение, классификация и принцип работы.
- •13 Классификация, свойства и характеристики теплоносителей.
- •14 Кабельные линии, конструкции, преимущества.
- •15 Магистральные и радиальные схемы электроснабжения сельскохозяйственных предприятий.
- •16 Как проводится консервация котла и выполняется защита от стояночной коррозии?
- •17 Проектирование проводок в производственных и общественных зданиях.
- •18 Виды и краткая характеристика потерь энергии и ресурсов в тепловых сетях.
- •19 Приемники электрической энергии, их основные характеристики.
- •20 Энергосбережение в котельных.
- •21 Вторичные энергоресурсы промпредприятий, используемые для генерации теплоты. Их количество, параметры, доля полезного использования в системах теплоснабжения.
- •22. Выбор сечения проводниковой арматуры (проводов, кабелей и шин) в электрических сетях.
- •24 Компрессорные машины. Назначение, область применения.
- •26 Виды электрических сетей.
- •27 Рабочий процесс газотурбинных установок (гту).
- •28 Надежность электроснабжения сельских потребителей.
- •29 Классификация газотурбинных установок.
- •31 Паровые турбины и их классификация.
- •32 Ректификационные установки: назначение, устройство и принцип работы.
- •33 Назначение, роль и место тепловых двигателей и нагнетателей.
- •34 Автоматизация и дистанционные управления – как средство повышения безопасности труда.
- •35 Параметры состояния газа. Уравнение состояния идеального газа. Первый закон термодинамики. Основные процессы идеального газа.
- •36 Абсорбционные установки: назначение, устройство и принцип работы.
- •37 Различия между идеальным газом и реальными газами. Фазовые переходы. Основные процессы с водяным паром. Использование водяного пара в технике.
- •38 Выпарные аппараты: назначение, устройство и принцип работы.
- •39 Газовые смеси. Влажный воздух и его параметры. Изображение на h-d диаграмме процессов сушки в конвективной сушилке и кондиционирования воздуха.
- •40 Качество электрической энергии.
- •41 Мероприятия по снижению потерь мощности и электроэнергии.
- •42 Равновесие капельной жидкости, движущейся прямолинейно и вращающейся вокруг вертикальной оси.
- •3.8. Равномерное вращение сосуда с жидкостью
- •43 Построение годового графика активной мощности.
- •44 Теория физического подобия. Три теоремы теории подобия. Критерии гидродинамического подобия.
- •45 Регулирование напряжения в электрических сетях.
- •46 Виды и образование скачков уплотнений. Уравнения скачков уплотнений.
- •47 Общие принципы энергосбережения в зданиях и сооружениях.
- •1 Бытовое энергосбережение
- •2 Структура расхода тепловой и электрической энергии зданиями
- •3 Тепловая изоляция зданий и сооружений
- •4 Совершенствование теплоснабжения. Тепловая изоляция трубопроводов.
- •5 Изоляционные характеристики остекления и стеклопакеты
- •48 Уравнение Бернулли для элементарной струйки идеальной жидкости. В чем состоит геометрический и энергетический смысл уравнения Бернулли.
- •49 Учет энергоресурсов: принципы и требования, предъявляемые к приборам учета тепловой и электрической энергии.
- •50 Поясните основные характеристики газовых потоков: число Маха, коэффициент скорости. Безразмерную скорость.
- •51 Смесительные аппараты: назначение, устройство и принцип работы.
- •53 Закон Фурье; коэффициент теплопроводности. Термическое сопротивление теплопроводности.
- •54 Классификация и параметры паровых и водогрейных котельных. Принцип выбора основного и вспомогательного оборудования.
- •55 Назначение и классификация тэц, используемых в системах теплоснабжения. Принципиальные тепловые схемы тэц.
- •57 Теплообменные аппараты. Уравнения теплового баланса и теплопередачи; средняя разность температур между теплоносителями. Расчет прямоточных и противоточных теплообменников.
- •12.5.Конструкторский и поверочный расчёт теплообменных аппаратов
- •58 Методы анализа травматизма и заболеваемости. Их показатели и прогнозирование.
- •59 Свободная и вынужденная конвекции; физические свойства жидкостей. Числа (критерии) подобия конвективного теплообмена.
- •60 Энергетические, экологические и экономические показатели котельных.
- •62 Требования безопасности к конструкции и эксплуатации теплотехнического оборудования.
- •63 Коэффициент теплофикации и определение его оптимального значения. Использование пиковых водогрейных котлов.
- •64 Назовите основные задачи обслуживания паровых и водогрейных котлов.
- •65 Котельные - основной источник генерации теплоты в системах теплоснабжения. Производственные и отопительные котельные. Их назначение и области рационального использования.
- •66 Требования безопасности к конструкции и эксплуатации сосудов, работающих под давлением.
- •67 Изоляционные конструкции теплопроводов. Методика их теплового расчета. Определение тепловых потерь участка тепловой сети и падения температур теплоносителя по их длине.
- •68 Технические средства безопасности, виды и защита работающих.
- •69 Лучистый теплообмен; законы Планка, смещения Вина, Стефана-Больцмана. Степень черноты тела; закон Кирхгофа и следствие из него.
- •70 Рекуперативные аппараты: назначение, устройство и принцип работы.
6 Суточные и сменные графики теплопотребления. Методика определения максимальных, средних и годовых потребностей в теплоте каждым типом потребителей.
Отопительная нагрузка имеет, как правило круглосуточный характер. При неизменных наружной тем-ре, скорости ветра и облачности, отопительная нагрузка зданий и пром.предприятий практически постоянна. Отопит нагрузка пром предприятий имеет непостоянный суточный и недельный график, когда в целях экономии теплоты искусственно снижают подачу теплоты на отопление в нерабочие часы(ночь и выходные). Параметры и расход теплоты для технологических нужд зависят от характера технологического процесса, типа производственного оборудования, общей организации работ и др. как правило тепловые нагрузки пром.предприятий задаются технологами на основе соответствующих расчётов или данных тепловых испытаний.
Графики нагрузок являются основополагающим звеном при расчете и проектировании систем энергообеспечения предприятия. Они дают ясную картину количественных и качественных изменений параметров конкретных энергоносителей за конкретный период времени. Графики нагрузок зависят от типа и назначения энергоносителя, а также от режима работы предприятия. Например, сезонный график тепловой нагрузки имеет неравномерный характер, обусловленный различными климатическими условиями в различное время года.
|
|
Сезонная нагрузка для данного региона имеет относительно постоянный характер. Примером сезонной нагрузки может служить отопление и вентиляция. Для характеристики количественных и качественных показателей графика вводится ряд понятий и обозначений: Qmax, Qmin, Qср, Qmax зим., Qmax лет. и т.д. Для характеристики зон графиков вводят понятие базовой части, переменной части и пиковой части. Базовая часть находится между осью и минимальной нагрузкой. Переменная часть находится между средней и минимальной нагрузкой. А пиковая часть - между средней и максимальной нагрузкой. Для описания характера изменения графика вводится ряд коэффициентов, в том числе: α – коэффициент неравномерности графика; γ – коэффициент заполнения графика; ki – интегральный коэффициент графика; |
tmax и tmin – число часов использования максимума и минимума нагрузки и т.д.
Эти коэффициенты используются при расчете и оптимизации системы энергообеспечения предприятия, расчете нагрузок и режимов и выбора параметров основного и вспомогательного оборудования.
Годовой расход теплоты на отопление определяют по формуле
QОГ = QОСР nО TО , ГДж/год,
где nО – число дней отопительного периода, сут.;
TО – время работы системы отопления в сутки, часов (при круглосуточной работе TО = 24 часа).
Часовой расход теплоты определяют по формуле
QО = Jt (tВ – tН.О) (VН qО ) 3,610-6,
где QО – часовой расход теплоты на отопление, ГДж/ч;
Jt - поправочный коэффициент, принимаемый в зависимости от
расчетной температуры наружного воздуха
7 Теплопроводность через плоские, цилиндрические, 1-слойные и многослойные стенки.
Теплопроводность – это перенос тепла от одних частей тела к другим обусловленный разновидностью температур. С физической точки зрения это молекулярный перенос.
Если внутри тела или материала имеется разность температур, то тепловая энергия переходит от более горячей его части к более холодной и передаёт ей свою тепло. Данный вид теплопередачи, который обусловлен тепловыми движениями и столкновениями молекул, называется теплопроводность. При достаточно высоких температурах в твердых телах его можно наблюдать визуально.
Виды теплопроводности Бывает:
-стационарная теплопроводность
-не стационарная теплопроводность
В общем случае процесс теплопереноса теплопроводностью сопровождается изменением температуры в пространстве и во времени.
Стационарное температурное поле – это если температура тела не изменяется с течением времени и зависит только от геометрических размеров тела.
Нестационарное температурное поле – это когда изменение температуры тела зависит от времени.
Количественная характеристика изменения температуры на бесконечно малом отрезке тела характеризует градиент температуры.
Градиент температуры математическими терминами – это предел изменения температуры к нормали, причём последнее стремиться к нулю.
Градиент – это вектор направленный к изометрической поверхности в сторону возрастания температуры и численно равен частной производной этой температуры по этому направлению.
1).Однородная плоская стенка (Рис.9.2.).

Температуры поверхностей стенки –tст1 и tст2.
Плотность теплового потока:
q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (tcт2 - tcт1)/(xcт2 - xcт1) или q = λ∙ (tcт2 - tcт1)/(xcт2 - xcт1)∙ Dt/Dx (9.13)
Тогда q = λ/δ∙(tст1 – tст2) = λ/δ∙Δt, (9.14)
Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м2∙К)/Вт], то плотность теплового потока:
q = (tст1 – tст2)/R . (9.15)
Общее количество теплоты, которое передается через поверхность F за время τ определяется:
Q = q∙F∙τ = (tст1 – tст2)/R·F∙τ . (9.16)
Температура тела в точке с координатой х находится по формуле:
tx = tст1 – (tст1 – tст2)∙x/ δ . (9.17)
2).Многослойная плоская стенка.
Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенок tст1 и tст2, коэффициенты теплопроводности слоев λ1, λ2, λ3, толщина слоев δ1, δ2, δ3.
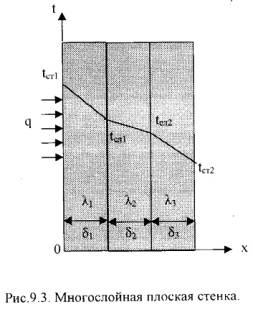
Плотности тепловых потокок через каждый слой стенки:
q = λ1/δ1∙(tст1 – tсл1) , (9.18)
q = λ2/δ2∙(tсл1 – tсл2) , (9.19)
q = λ3/δ3∙(tсл2 – tст2) , (9.20)
Решая эти уравнения, относительно разности температур и складывая, получаем:
q = (t1 – t4)/(δ1/λ1 + δ2/λ2 + δ3/λ3) = (tст1 – tст4)/Ro , (9.21)
где: Ro = (δ1/λ1 + δ2/λ2 + δ3/λ3) – общее термическое сопротивление теплопроводности многослойной стенки.
Температура слоев определяется по следующим формулам:
tсл1 = tст1 – q∙(δ1/λ1). (9.22)
tсл2 = tсл1 – q·δ2/λ2). (9.23)
Цилиндрические стенки.
1). Однородная
цилиндрическая стенка.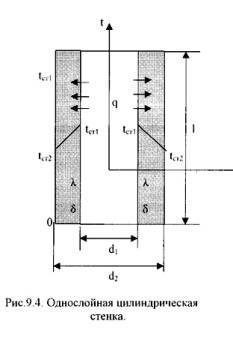
Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d1и внешним диаметром d2 (Рис.9.4).
Температуры поверхностей стенки – tст1 и tст2.
Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d2/d1), (9.25)где: Δt = tст1 – tст2 – температурный напор;
λ – κоэффициент теплопроводности стенки.
Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут: ql = Q/l =2·π·λ·Δt /ln(d2/d1), [Вт/м]. (9.26)
Температура тела внутри стенки с координатой dх:tx = tст1 – (tст1 – tст2) ·ln(dx/d1) / ln(d2/d1). (9.27)2). Многослойная цилиндрическая стенка.
Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).
Температура
внутренней поверхности стенки – tст1,
температура наружной поверхности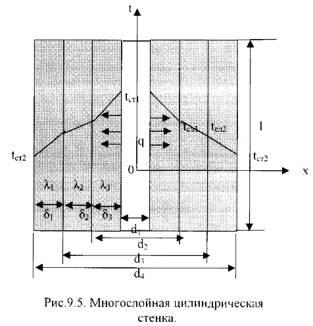
стенки –tст2, коэффициенты теплопроводности слоев -λ1, λ2, λ3, диаметры слоев d1, d2, d3, d4.
Тепловые потоки для слоев будут:
1-й слойQ = 2·π· λ1·l·(tст1 – tсл1)/ ln(d2/d1), (9.28)
2-й слой
Q = 2·π·λ2·l·(tсл1 – tсл2)/ ln(d3/d2), (9.29)
3-й слой
Q = 2·π·λ3·l·(tсл2 – tст2)/ ln(d4/d3), (9.30)
Решая полученные уравнения, получаем
для теплового потока через многослойную стенку:
Q = 2·π·l·(tст1 – tст2) / [ln(d2/d1)/λ1 + ln(d3/d2)/λ2 + ln(d4/d3)/λ3]. (9.31)
Для линейной плотности теплового потока имеем: ql = Q/l = 2·π· (t1 – t2) / [ln(d2/d1)/λ1 + ln(d3/d2)/λ2 + ln(d4/d3)/λ3]. (9.32)
Температуру между слоями находим из следующих уравнений
tсл1 = tст1 – ql·ln(d2/d1) / 2·π·λ1 . (9.33)
tсл2 = tсл1 – ql·ln(d3/d2) / 2·π·λ2 . (9.34)

