DM.III

Теорема 3.11.7 (Понтрягин-Куратовский). Граф является планарным тогда и только тогда, когда он не содержит подграфа, гомеоморфного одному из графов Понтрягина-Куратовского.

П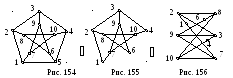 ользуясь сформулированной теоремой, покажем, например, что граф Петерсена (рис. 154) не является планарным. Докажем для этого, что он имеет подграф, гомеоморфный . Оба эти графа являются однородными кубическими, но граф Петерсена имеет 10 вершин, а граф – только 6.

В графе Петерсена удалим вершину 5 вместе с примыкающими к ней ребрами (рис. 155). Полученный после этой операции подграф изобразим так, как показано на рис. 156. Из рисунка видно, что этот подграф гомеоморфен графу . Значит, граф Петерсена не является планарным.

Рассмотренный пример показывает, что на практике проверка выполнения условий планарности может оказаться достаточно сложной задачей. В некоторых случаях решение этой задачи облегчает другой критерий планарности, который можно доказать опираясь на теорему Понтрягина-Куратовского.

Теорема 3.11.8. Граф является планарным тогда и только тогда, когда он не имеет подграфов, которые стягиваются до графов или .

Если в графе Петерсена последовательно стянуть ребра (1, 7), (2, 8), (3, 9), (4, 10), (5, 6), получим граф . Поэтому, пользуясь новым критерием, сразу заключаем, что граф Петерсена не является планарным.

В общем случае разработано несколько эффективных алгоритмов, позволяющих для любого графа шаг за шагом стоить его плоскую укладку, а после первого же невыполнимого шага сразу заключить, что граф непланарен.

6. Реберные пересечения. Как уже отмечалось, при монтаже электронных схем важно знать, какое наименьшее число плат может потребоваться для комплектования всей схемы. При отыскании ответа на этот вопрос вводятся понятия числа скрещиваний и толщины графа.

Ч ислом скрещиваний графа называется наименьшее возможное число пересечений ребер этого графа, получаемых при его изображении на плоскости.

Число скрещиваний графа является мерой его «непланарности». Очевидно, что для планарного графа оно равно нулю. Для графов Понтрягина-Куратовского (рис. 157).

В качестве примера укажем оценку числа скрещиваний для полных графов. Предположим, что на плоскости задана некоторая плоская триангуляция G, содержащая вершин (). Если соединить ребрами все пары вершин, не инцидентные в графе G, то получим полный граф , являющийся сверхграфом для G и имеющий столько же вершин, что и G. Так как полный граф с вершинами имеет ребер, а для плоской триангуляции с тем же количеством вершин , то для того чтобы из графа G получить полный граф необходимо добавить

ребер.

Если исходная триангуляция G являлась полным графом, то она совпадает со своим пополнением и . Последнее равенство возможно лишь для и . Другими словами, лишь полные графы с тремя и четырьмя вершинами являются плоскими триангуляциями (рис. 158).

Заметим, что полные графы с одной (точка) и двумя вершинами (отрезок) так же являются плоскими, но не являются плоскими триангуляциями.

При добавлении к плоской триангуляции G хотя бы одного ребра получится граф , который не является плоским. Поэтому его укладка на плоскости станет «неправильной» – появятся реберные пересечения. Ясно, что минимальное количество реберных пересечений в полном графе не меньше числа :

.

Так, например, минимальное количество реберных пересечений для графа равно 3 (рис. 159), что согласуется с неравенством .

Отметим, что число скрещиваний для будет строго больше числа . Это связано с тем, что каждое новое ребро, добавляемое к графу, может иметь не одно, а несколько пересечений с другими ребрами. Более точную оценку числа скрещиваний в полных графах для дают следующие выражения, полученные Т.Саати (см. [2]):

Толщиной графа называется наименьшее число планарных графов, объединение которых дает .

 Отображение фигуры на фигуру называется гомеоморфным, если оно имеет обратное отображение , и оба отображения и непрерывны.

 Внутренность каждой грани, за исключением внешней грани, гомеоморфна внутренности круга, а внешняя грань без границы гомеоморфна внешности круга.

 Многогранник называется простым, если его поверхность гомеоморфна сфере, т.е. имеет нулевой род.

139