
- •Минобрнауки россии
- •Тема 1. Функция действительного аргумента
- •Тема 2. Дифференциальное исчисление
- •Тема 3. Интегральное исчисление
- •Тема 4. Дифференциальные уравнения
- •Тема 5. Функции нескольких переменных
- •Тема 6. Ряды
- •Б) Основная литература
- •В) Дополнительная литература
- •4..Задания для контрольной работы
Б) Основная литература
3. Баврин И.И., Матросов В.Л. Общий курс высшей математики М. Просвещение, 2010.
4. Берман Г. Н. Сборник задач по курсу математического анализа. СПб.: Профессия, 2011.
5. Высшая математика для экономистов / под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2009.
6. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 2008.
В) Дополнительная литература
7. Бохан А. и др. Курс математического анализа, ч.1,2. М. Просвещение, 2010.
8. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа (под редакцией А.В. Ефимова и Б.П. Демидовича) – М.: Наука, 2009.
9. Ильин В., Поздняк Э. Основы математического анализа, ч.1,2. М.Наука, 2010г.
10. Рудаков И.А. Лекции по высшей математике. Ч. 1, 2. Брянск, 2010.
3 РЕШЕНИЕ ЗАДАЧ НУЛЕВОГО ВАРИАНТА
Найти
предел последовательности, общий член
которой
 .
.
Решение.
Разделим
числитель и знаменатель дроби на
 ,
получим:
,
получим:
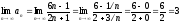 .
.
Замечание.
 и предел постоянной равен самой
постоянной.
и предел постоянной равен самой
постоянной.
Найти
 .
.
Решение.
Поскольку
 и
и ,
то
,
то

Найти
производную функции
 .
.
Решение.
Применяя формулы дифференцирования, получим
 .
.
Найти
производную функции
 .
.
Решение.
На основе формул дифференцирования находим

Найти
производную функции
 .
.
Решение.
Применяя формулы дифференцирования, получим

Найти
производную функции
 .
.
Решение.
Аргументом
данной функции является не
 ,
а
,
а .
Это сложная тригонометрическая функция,
которую можно представить так:
.
Это сложная тригонометрическая функция,
которую можно представить так:
 .
.
Поскольку
 ,
то получаем
,
то получаем .
.
Найти
вторую производную функции
 .
.
Решение.
Находим сначала первую производную данной функции:
 .
.
Дифференцируя
ее еще раз, получаем
 .
.
Найти
промежутки возрастания и убывания
функции
 .
.
Решение.
Данная
функция определена при всех
 ,
областью ее определения является
бесконечный промежуток
,
областью ее определения является
бесконечный промежуток .
Производная этой функции
.
Производная этой функции


обращается
в нуль в трех точках:
 ,
которые делят область определения на
четыре интервала:
,
которые делят область определения на
четыре интервала: .
.
Поскольку
 при
при ,
то функция возрастает в промежутке
,
то функция возрастает в промежутке .
.
Так
как
 при
при ,
то функция убывает в промежутке
,
то функция убывает в промежутке .
.
Аналогично
устанавливаем, что в промежутке
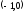 функция возрастает (ибо
функция возрастает (ибо при
при ),
в промежутке
),
в промежутке она также возрастает (
она также возрастает ( при
при ).
).
Найти
экстремумы функции
 .
.
Решение.
Производная
данной функции
 определена для всех
определена для всех и обращается в нуль при
и обращается в нуль при .
Исследуем эти критические точки с
помощью второй производной
.
Исследуем эти критические точки с
помощью второй производной .
.
Поскольку
 ,
то
,
то - точка максимума; так как
- точка максимума; так как ,
то
,
то - точка минимума.
- точка минимума.
Вычисляем значения экстремумов:

Найти
наибольшее и наименьшее значения функции
 на отрезке
на отрезке .
.
Решение.
Находим экстремумы функции:

 -
точки минимума,
-
точки минимума,
 - точка максимума,
- точка максимума, .
.
Находим значения функции на концах отрезка:
 .
.
Следовательно, наименьшее значение функции на данном отрезке равно 2, а наибольшее равно 11.
Найти
промежутки выпуклости и точки перегиба
графика функции
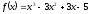 .
.
Решение.
Найти производные данной функции:

Вторая
производная равна нулю при
 .
Если
.
Если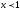 ,
то
,
то ,
поэтому график функции является выпуклым
вверх в промежутке
,
поэтому график функции является выпуклым
вверх в промежутке .
Поскольку
.
Поскольку при
при ,
то график функции является выпуклым
вниз в промежутке
,
то график функции является выпуклым
вниз в промежутке .
Так как при
.
Так как при вторая производная меняет знак, то
вторая производная меняет знак, то - точка перегиба графика функции
- точка перегиба графика функции .
.
Найти
асимптоты графика функции
 .
.
Решение.
Поскольку

то
уравнение
 определяет вертикальную асимптоту
графика данной функции.
определяет вертикальную асимптоту
графика данной функции.
Так
как
 ,
где
,
где при
при ,
то уравнение
,
то уравнение определяет невертикальную асимптоту
графика данной функции.
определяет невертикальную асимптоту
графика данной функции.
Исследовать
функцию
 и построить ее график.
и построить ее график.
Решение.
Областью определения данной функции является бесконечный промежуток
 .
.Функция неограниченно возрастает при
 ,
т.е.
,
т.е.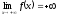 ,
далее
,
далее .
.Производная данной функции
 обращается в нуль при
обращается в нуль при .
Так как
.
Так как при
при ,
то функция возрастает в промежутках
,
то функция возрастает в промежутках .
Поскольку
.
Поскольку при
при ,
то функция убывает в промежутке
,
то функция убывает в промежутке .
Отсюда уже можно заключить, что при
.
Отсюда уже можно заключить, что при - точка максимума,
- точка максимума,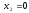 - точка минимума.
- точка минимума.Подставляя значения
 в выражение для функции, вычисляем ее
экстремальные значения:
в выражение для функции, вычисляем ее
экстремальные значения:

Получаем
две точки графика
 .
.
Вторая производная
 обращается в нуль при
обращается в нуль при .
Так как
.
Так как при
при ,
то график функции является выпуклым
вверх в промежутке
,
то график функции является выпуклым
вверх в промежутке ;
поскольку
;
поскольку при
при ,
то график функции является выпуклым
вниз в промежутке
,
то график функции является выпуклым
вниз в промежутке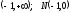 - точка перегиба графика.
- точка перегиба графика.Решая уравнение
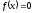 ,
т.е.
,
т.е. ,
находим нули функции:
,
находим нули функции:
 ,
,
поэтому
 - точки пересечения графика функции с
осью
- точки пересечения графика функции с
осью .
Положив в выражении
.
Положив в выражении ,
получим
,
получим - точка пересечения с осью
- точка пересечения с осью ,
она совпадает с точкой
,
она совпадает с точкой .
.
7)
Поскольку
 ,
т.е. не существует конечных пределов,
то график данной функции асимптот не
имеет.
,
т.е. не существует конечных пределов,
то график данной функции асимптот не
имеет.
Отметив полученные точки и приняв во внимание указанные результаты исследования функции, строим график.
Найти
неопределенный интеграл

Решение.
Разделив почленно числитель на знаменатель, используя свойства неопределенного интеграла, находим



Найти
 .
.
Решение.
Раскрывая скобки и применяя формулы, получаем

Найти
 .
.
Решение.
Поскольку
 ,
то
,
то .
.
Найти
 .
.
Решение.
Введем
новую переменную по формуле
 ,
откуда
,
откуда или
или .
Подставляя полученные выражения в
подынтегральное выражение, находим
.
Подставляя полученные выражения в
подынтегральное выражение, находим
 .
.
Снова
переходя к переменной
 ,
получаем
,
получаем
 .
.
Найти
 .
.
Решение.
Чтобы
избавиться от иррациональности, положим
 ,
откуда
,
откуда .
.
 .
.
Переходя
к переменной
 ,
получаем
,
получаем
 .
.
Вычислить
определенный интеграл
 .
.
Решение.
Принимая во внимание свойства определенного интеграла, находим
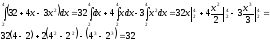
Вычислить
значения частных производных функции
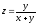 в точке
в точке
 .
.
Решение.
Найдем сначала выражения для частных производных.
Считая
 постоянным
и дифференцируя по
постоянным
и дифференцируя по частное, получаем:
частное, получаем:
 .
.
Считая
 постоянным и дифференцируя по
постоянным и дифференцируя по ,
находим:
,
находим:
 .
.
В
полученные выражения подставим значения
 :
:
 ,
,
 .
.
Решить
дифференциальное уравнение
 .
.
Решение.
Характеристическое
уравнение
 имеет кратный корень
имеет кратный корень ,
поэтому частное решение данного уравнения
ищем в виде
,
поэтому частное решение данного уравнения
ищем в виде .
.
Поскольку
 ,
,
то
 ,
,
 ,
,
то есть
 .
.
Так
как
 ,
то общее решение данного уравнения
определяется формулой
,
то общее решение данного уравнения
определяется формулой
 .
.
Записать
первые пять членов ряда, общий член
которого задан формулой
 .
.
Решение.
Полагая
в данной формуле
 ,
получаем:
,
получаем:

Следовательно,

