1.3 Постановки задач для уравнений параболического типа

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В однородной среде (без источников энергии) уравнение теплопроводности или диффузии имеет вид

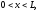
(1.17)

где u – температура, k – коэффициент теплопроводности, c – удельная теплоемкость,- плотность (в задаче диффузии u – концентрация диффундирующего вещества,d - коэффициент диффузии, c – коэффициент пористости среды, который определяется отношением объема пор к рассматриваемому объему), x=0 и x=L левый и правый концы отрезка изменения пространственной переменной, t=0 и t=T – моменты начала и окончания процесса. На множестверассматриваются различные начально-краевые задачи для уравнения (4) (рис. 1.1)

Рис. 1.1 - Область D ограниченная прямоугольником

Первая начально-краевая задача:

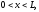
(1.18)

(начальное условие)

(краевое условие на левой границе)

(краевое условие на правой границе)

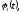
содержит функциональное начальное условие (при t=0) и функциональные краевые условия на левой (x=0) и правой (x=L) границах области. Где – заданные функции.

Вторая начально-краевая задача:

(1.19)

(начальное условие)

(краевое условие на левой границе)

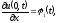
(краевое условие на правой границе)

содержит функциональное начальное условие (при t=0) и дифференциальные краевые условия на левой (x=0) и правой (x=L) границах области.

Третья начально-краевая задача:

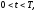(1.20)

(начальное условие)

(краевое условие на левой границе)

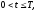(краевое условие на правой границе)

содержит функциональное начальное условие (при t=0) и функционально-дифференциальные краевые условия на левой (x=0) и правой (x=L) границах области. Где – заданные числа.

Задача Коши:

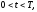
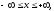(начальное условие)

содержит только функциональное начальное условие (при t=0) и рассматривается в бесконечной области изменения пространственной переменной.

Примером физической задачи, приводящей к первой начально-краевой задаче служит процесс теплопередачи по длинному тонкому стержню, лежащему вдоль оси Ox от x=0 до x=L (ось стержня совпадает с осью Ox). Предполагается, что в точке x=0 температура изменяется со временем по законуа в точке x=L по законуВ начальный момент времени при t=0 функциейзадано начальное распределение температуры вдоль стержня. Тогда распределение температуры вдоль него во все последующие моменты времени определяется решением начально-краевой задачи с уравнением (1.7), где– температура стержня в некоторой точке x в момент времени t.

Во всех перечисленных задачах требуется найти функцию 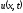, которая удовлетворяет дифференциальному уравнению (1.7) в области D и соответствующим условиям на ее границе.

2. Численное решение дифференциальных уравнений

2.1 Основные определения и конечно-разностные схемы для дифференциальных уравнений параболического типа

2.1.1 Основные определения. Принцип построения разностных схем

Точное решение задач математической физики (в виде явных формул, рядов и т.п.) можно найти только в редких случаях. Среди приближенных методов, наиболее применимы разностные методы (методы сеток). Сущность разностных методов состоит в том, что исходная область изменения независимых переменных заменяется дискретным множеством точек – сеток, а производные, входящие в уравнение, аппроксимируются на этой сетке разностными соотношениями. В результате исходная линейная задача заменяется системой конечного числа линейных алгебраических уравнений, называемой разностной схемой (задачей), а исходная нелинейная задача заменяется нелинейной разностной схемой. За приближенное решение исходной задачи принимается решение разностной схемы. Точность приближения зависит от способа аппроксимации и от густоты сетки.

Пусть дана исходная (дифференциальная) задача в виде

(2.1)

где u – искомая функция, определенная на множестве Г; D – область пространства независимых переменных с границей Г; f – заданная функция, L – линейный дифференциальный оператор. Все производные, входящие в дифференциальной уравнение, перенесены в левую часть, а остальные функции образуют правую часть; дополнительные условия (начальные и краевые) также включены, а оператор и правую часть f.

Для численного решения задачи вводится сетка – конечное множество точек Mh (узлов сетки), принадлежащих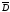, плотность размещения которых характеризуется параметром h - шагом сетки. В общем случае h – вектор, компонентами которого являются шаги по всем независимым переменным решаемой задачи, с длиной. Обычно сетка задается так, что примножество Dh стремится заполнить множествоГ.

Рассмотрим некоторую дифференциальную задачу с двумя независимыми переменными x и t. Для простоты изложения множество D представляет собой прямоугольник длины l и высоты T, ограниченный отрезками прямых, параллельных осям Ox и Ot (рис. 2.1), т. е. задана двумерная прямоугольная сетка

,

где,;, N, K – целые положительные числа; h,- величины шагов по пространству и времени (для простоты принимаются постоянными);,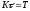. Такая сетка называется равномерной (регулярной). В данном случаеили. Узлы, принадлежащие промежуткам,, называются граничными, а остальные – внутренними. Слоем,;называется множество всех узлов сетки, имеющих одну и ту же временную координату

Рис. 2.1 - Конечно-разностная сетка

Функции, определенные в точках сетки , называются сеточными. Введем сеточную функцию

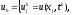
, (2.2)

с пространственным шагом и шагом по времени(рис. 2.1). Данная функция является сеточным представлением решения исходной (дифференциальной) задачи или точным решением дифференциальной задачи в узлах сетки. Вычислитьне удается, поэтому находят другую сеточную функцию, приближенно совпадающую с точным решением в узлах сетки. Она вычисляется как решение разностной схемы

(2.3)

в некотором смысле соответствующей задаче (2.1). Здесь Lh – разностный оператор, аппроксимирующий линейный дифференциальный оператор B (он формируется в результате аппроксимации частных производных, входящих в B, соответствующими конечно-разностными соотношениями); 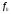- сеточная функция, возникающая в результате замены правой части уравнения (2.1) значениями в узлах сетки. Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные условия (начальные и краевые) – в граничных узлах. Разностную схему будем называть разностной задачей по аналогии с дифференциальной задачей.

Введем на конечно-разностной сетке (2.2) два временных слоя: нижний , на котором распределение искомой функции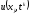,,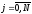 и верхний временной слой, на котором распределение искомой функции,подлежит определению.

На введенной сетке (2.2) введем сеточные функции ,,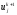 первая из которых известна, вторая – подлежит определению. Для ее определения в задаче (1.18) заменим (аппроксимируем) дифференциальные операторы отношением конечных разностей, получим

, (2.4)

(2.5)

Подставляя (2.4), (2.5) в задачу (1.18), получим явную конечно-разностную схему для этой задачи в форме

, ,;

, ,(2.6)

, .

В каждом уравнении этой задачи все значения сеточной функции известны, за исключением одного, , которое может быть определено явно из соотношений (2.6). В соотношения (2.6) краевые условия входят при значениях j=1 и j=N–1, а начальное условие – при k=0.

Определение 1. Схема называется явной, если оператор L аппроксимируется с использованием известных значений функции на n-м слое, а аппроксимирующее уравнение содержит только одно неизвестное значение функции на следующемм слое, которое нетрудно выразить явно.

Если в (2.5) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое:

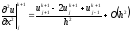
(2.7)

то после подстановки (2.4), (2.7) в задачу (1.18), получим неявную конечно-разностную схему для этой задачи:

, ,;

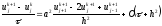, ,(2.8)

, .

Теперь сеточную функцию на верхнем временном слое можно получить из решения СЛАУ (2.8) с трехдиагональной матрицей.

Определение 2. Схема называется неявной, если оператор аппроксимируется с использованием нескольких неизвестных значений искомой функции на м слое.

Узлы сетки , значения в которых используется при аппроксимации оператора B, образуют шаблон.

Шаблоном конечно-разностной схемы называют ее геометрическую интерпритацию на конечно-разностной сетке.

При изображении шаблона светлыми кружочками обозначаются узлы на k-м слое с известными значениями функции, а зачеркнутыми – узлы на м слое с неизвестными значениями функции, подлежащие определению. Шаблон, содержащий p узлов, называется p-точечным.

На рис. 2.2 приведены шаблоны для явной (2.6) и неявной (2.8) конечно-разностных схем при аппроксимации задачи (1.18).

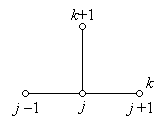
а б

Рис. 2.2 - Шаблоны явной (а) и неявной (б) конечно-разностных схем для уравнения теплопроводности