2.2.3 Метод дробных шагов н.Н. Яненко

В отличие от МПН, метод дробных шагов (МДШ) использует только неявные конечно-разностные операторы, что делает его абсолютно устойчивым в задачах, не содержащих смешанных производных. Он обладает довольно значительным запасом устойчивости (сохранение устойчивости при числах Куранта, значительно превышающих единицу) и в задачах со смешанными производными.

Схема МДШ имеет вид

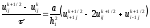, (2.77)

. (2.78)

С помощью чисто неявной подсхемы (2.77) осуществляются скалярные прогонки в направлении оси х в количестве, равном J-1, в результате чего получаем сеточную функцию . На втором дробном шаге по времени с помощью подсхемы (2.78) осуществляются скалярные прогонки в направлении оси у в количестве, равном I-1, в результате чего получаем сеточную функцию. Шаблон схемы МДШ приведен на рис. 2.5. Для определения порядка аппроксимации схемы МДШ запишем ее в следующей операторной форме:

, ,

, ,

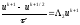Рис. 2.5 - Шаблон схемы метода дробных шагов

Исключая здесь сеточную функцию на промежуточном временном слое , получим двухслойную схему, откуда получаем порядок аппроксимации по времени:

,

. (2.79)

Из (2.79) видно, что схема МДШ (2.77), (2.78) имеет порядок , т.е. первый порядок по времени и второй - по переменным х и у.

Для исследования устойчивости схемы МДШ (2.77), (2.78) подставим в нее гармонику , получим

, ;

, .

Тогда отношение амплитуд гармоник равно

,

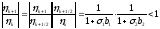т. е. схема метода дробных шагов абсолютно устойчива.

Достоинства схемы МДШ: 1) проста в алгоритмизации и программировании; 2) абсолютно устойчива с большим запасом устойчивости даже для задач, содержащих смешанные производные.

Недостатки: 1) на каждом дробном шаге достигается частичная аппроксимация, полная аппроксимация достигается на последнем дробном шаге; 2) имеет первый порядок точности по времени; 3) в задачах со смешанными производными для устойчивости МДШ на коэффициенты накладываются жесткие ограничения, при невыполнении которых схема становится условно устойчивой.

2.2.4 Метод переменных направлений с экстраполяцией в. Ф. Формалева

Как видно из изложенных выше конечно-разностных схем для многомерных задач математической физики, конечно-разностная схема может быть либо абсолютно устойчивой, но не экономичной (метод матричной прогонки), либо экономичной, но условно устойчивой, как схема МПН. Желание получить схемы экономичные и одновременно абсолютно устойчивые с большим запасом устойчивости приводит к необходимости использовать апостериорную информацию о сеточной функции, которая получается в процессе счета. К таким схемам относится схема метода переменных направлений с экстраполяцией (МПНЭ). Эта схема использует распределение сеточной функции в левом (от расчетного) пространственном сечении, уже полученное на верхнем временном слое, т. е. неявно. В правом пространственном сечении значения сеточной функции в первом приближении и с контролируемой точностью определяются линейной экстраполяцией по времени с нижних временных слоев на верхний. Затем эти значения уточняются с помощью скалярных прогонок.

Рассмотрим задачу, в которой дифференциальное уравнение ,,,содержит смешанные производные (наличие последних не обязательно):

, ,,. (2.80)

На сетке аппроксимируем это дифференциальное уравнение с помощью следующей схемы:

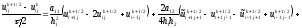
, (2.81)

, (2.82)

Здесь значения сеточной функции , помеченные волнистой чертой, определяются с помощью линейной экстраполяции:

, ,

, .

Шаблон схемы МПНЭ представлен на рис. 2.6.

Рис. 2.6 - Шаблон схемы метода переменных направлений с экстраполяцией: а - подсхема (2.81); б - подсхема (2.82)

В подсхеме (2.81) значени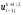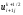я ,,являются искомыми, определяемыми из скалярных прогонок в направлении переменной х , значения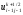,,уже известны на верхнем полуслое из прогонки вдоль координатной линии, а значения,,с порядкомопределяются экстраполяцией по распределениям функции на двух предыдущих временных полуслоях. При этом все конечно-разностные операторы по пространственным переменным, за исключением оператора по переменной х, переводятся в правые части (хотя они и являются практически полностью неявными).

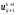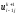В подсхеме (2.82) значения ,,являются искомыми, определяемыми из скалярных прогонок вдоль переменной у, значения,,известны как значения сеточной функции в левом пространственном сечении, а значения,,с порядкомопределяются экстраполяцией по двум предыдущим временным полуслоям. При этом все пространственные операторы, за исключением оператора по переменной у, переводятся в правые части, хотя они практически являются полностью неявными.

Аппроксимация. Для анализа аппроксимационных свойств схемы (2.81), (2.82) прибавим и вычтем в подсхеме (2.81)

Выражения ,, получим эквивалентную схему

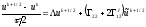, (2.83)

, (2.84)

где ,,

, ,

, ,

, .

Справедлива следующая теорема.

Теорема 1. Пусть решение задачи (2.80), (.2)-(.6) , где,,- класс функций, т раз непрерывно дифференцируемых по t и п раз - по х, у. Тогда схема (2.81), (2.82) и, следовательно, эквивалентная ей схема (2.83), (2.84) аппроксимирует на точном решении дифференциальную задачу (2.80) с порядком, где. Доказательство. Действительно, рассматривая «осколочные» операторы,,,, можно заметить, что выполняются следующие тождества:

,

,

,

,

, ,

, ,,

, ,,,.

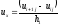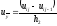Тогда справедлива следующая цепочка равенств:

.

Таким образом,

. (2.85)

Аналогично,

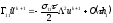(2.86)

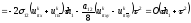; (2.87)

. (2.88)

Подставляя выражения (2.85)-(2.88) для «осколочных» операторов в схему (2.83), (2.84) , получим

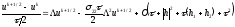(2.89)

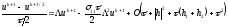(2.90)

Исключение сеточной функции на промежуточном временном полуслое приводит к следующей эквивалентной двухслойной схеме:

(2.91)

где ,.

Из (2.91) следует аппроксимация с порядком 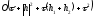. Теорема доказана.

Устойчивость. Будем исследовать устойчивость схемы (2.81), (2.82) методом энергетических неравенств.

Имеет место следующая теорема.

Теорема 2. Пусть выполнены условия ,. Тогда схема (2.81), (2.82) абсолютна устойчива по начальным условиям.

Для доказательства этой теоремы докажем следующую лемму.

Лемма. Оператор

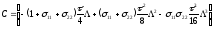
в эквивалентной схеме (2.91) является положительно определенным и самосопряженным.

Действительно, этот оператор можно переписать в виде

,

и котором каждое слагаемое является положительно определенным и самосопряженным оператором, поскольку - положительный, самосопряженный оператор, действующий в гильбертовом пространстве Н . Следовательно, оператор С является положительно определенным, самосопряженным оператором, что доказывает лемму.

Таким образом, (2.91) можно переписать в виде

.

Умножая это равенство скалярно на и используя известные тождества

,

получим следующее энергетическое тождество:

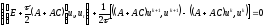, (2.92)

при выводе которого использована положительность и самосопряженность оператора .

Вводя энергетическое пространство элементовсо скалярным произведениеми нормой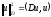, в силу положительности оператораиз (2.92) получаем энергетическое неравенство

откуда следует принцип максимума

,

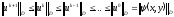являющийся достаточным признаком устойчивости конечно-разностной схемы (2.81), (2.82), что доказывает теорему.

Поскольку не накладывалось никаких ограничений на сеточные характеристики , схема (2.81), (2.82) является абсолютно устойчивой.

По запасу устойчивости метод МПНЭ превосходит все существующие экономичные методы расщепления для задач как содержащих, так и не содержащих смешанные дифференциальные операторы.

К достоинствам МПНЭ можно отнести следующие: 1) экономичность; 2) абсолютную устойчивость; 3) полную (не частичную, как в МДШ) аппроксимацию дифференциального уравнения; 4) применимость к задачам с любой размерностью по пространственным переменным и к задачам, содержащим смешанные дифференциальные операторы; 5) отсутствие ограничений на величину коэффициентов , кроме ограничений.