2.2 Конечно-разностный метод решения задач для уравнений параболического типа

2.2.1 Однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные

В задачах математической физики вообще, и в задачах теплопроводности в частности, граничные условия 1-го рода аппроксимируются точно в узлах на границе расчетной области и этот факт никак не влияет на порядок аппроксимации во всей расчетной области. Этого нельзя сказать об аппроксимации граничных условий 2-го и 3-го родов, поскольку в них присутствует производная первого порядка искомой функции по пространственной переменной, в результате чего порядок аппроксимации в граничных узлах может быть ниже порядка аппроксимации во внутренних узлах расчетной области.

В этой связи необходимо ввести понятия локального порядка аппроксимации - порядка аппроксимации в отдельно взятом узле, и глобального порядка аппроксимации - порядка аппроксимации во всей расчетной области. Для задач с граничными условиями 1-го рода на равномерной сетке локальный порядок аппроксимации совпадает с глобальным.

Для задач с граничными условиями, содержащими производные, порядок аппроксимации в граничных узлах может быть ниже порядка аппроксимации во внутренних узлах, если конечно-разностная схема в граничных узлах не использует дифференциальное уравнение (ниже будет показано, что в этом случае нарушается консервативность). Тогда глобальный порядок аппроксимации равен наименьшему относительно всех узлов сетки порядку аппроксимации.

Рассмотрим методологию сохранения на границах с граничными условиями 2-го и 3-го родов порядка аппроксимации, который дает аппроксимация дифференциального уравнения во внутренних узлах, т.е. получение конечно-разностной схемы с однородной аппроксимацией. Для этого рассмотрим третью начально-краевую задачу для уравнения теплопроводности, содержащего как конвективные члены (пропорциональные производной ), так и источниковые члены, содержащие искомую функцию: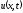

Во внутренних узлах конечно-разностной сетки (2.2) неявная конечно-разностная схема для уравнения (2.54) имеет вид

. (2.58)

Если производные первого порядка в граничных условиях (2.55) и (2.56) аппроксимировать по следующей схеме (с помощью отношения конечных разностей справа и слева):

;

.

то граничные условия аппроксимируются с первым порядком, и глобальный порядок будет равен первому порядку, несмотря на то, что во всех остальных узлах порядок аппроксимации по пространственной переменной равен двум. Для сохранения порядка аппроксимации, равного двум, в граничных узлах разложим на точном решении значение в окрестности точки х = 0 в ряд Тейлора по переменной х до третьей производной включительно, a- аналогичный ряд в окрестности точки х = l, получим (в предположении что функцияв граничных узлах имеет первые производные по времени и вторые - по х):

, (2.59)

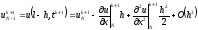. (2.60)

Подставим сюда значения второй производной в граничных узлах, полученные из дифференциального уравнения (2.54):

,

и найдем из полученных выражений (2.59), (2.60) значения первой производной в граничных узлах с порядком:

,

.

Подставляя в (2.55), а(2.56) и аппроксимируя полученные соотношения в соответствующих граничных узлах (при,), получим алгебраические уравнения для граничных узлов, в каждом из которых два неизвестных:

, ; (2.61)

, ;;

;

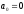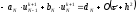, ; (2.62)

, ;;

.

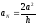Таким образом, (2.61) - конечно-разностная аппроксимация граничного условия 3-го рода (2.55) на левой границе х = 0, а (2.62) - конечно-разностная аппроксимация граничного условия 3-го рода (2.56) на правой границе х = l, которые сохраняют тот же порядок аппроксимации, что и в конечно-разностной аппроксимации (2.58) дифференциального уравнения (2.54).

Приписывая к граничным конечно-разностным уравнениям (2.61), (2.62), каждое из которых содержит два значения сеточной функции, алгебраические уравнения (2.58), записанные в виде

, ; (2.63)

; ;;,

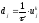получим СЛАУ с трехдиагональной матрицей, решаемой методом прогонки (;)

; (2.64)

, ;

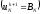, (2.65)

Рассмотрим более подробно метод матричной прогонки.

Метод применим в случае, когда матрица Р - трехдиагональная. Общая постановка задачи имеет следующий вид.

Дана система линейных алгебраических уравнений с трехдиагональной матрицей Р. Развернутая запись этой системы имеет вид

, ,, (2.66)

которому соответствует расширенная матрица

.

Здесь первое и последнее уравнения, содержащие по два слагаемых, могут рассматриваться как краевые условия. Знак «минус» при коэффициенте 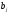, взят для более удобного представления расчетных формул метода.

Требуется найти решение системы (2.66) методом исключения Гаусса.

Если к (2.66) применить алгоритм прямого хода метода Гаусса, то вместо 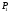получится:

Учитывая, что последний столбец в этой матрице соответствует правой части, и переходя к системе, включающей неизвестные, получаем рекуррентную формулу:

, . (2.67)

Соотношение (2.67) есть формула для обратного хода, а формулы для коэффициентов ,, которые называются прогоночными, определяются из (1.4), (2.67). Запишем (2.67) для индекса: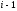

и подставим в (2.66). Получим

.

Приводя эту формулу к виду (2.67) и сравнивая полученное выражение с (2.67), получаем рекуррентные соотношения для ,:

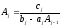, ,(2.68)

Определение прогоночных коэффициентов по формулам (2.68) соответствует прямому ходу метода прогонки.

Обратный ход метода прогонки начинается с вычисления хп. Для этого используется последнее уравнение, коэффициенты которого определены в прямом ходе, и последнее уравнение исходной системы:

,

Тогда определяется хп:

, т.е. . (2.69)

Остальные значения неизвестных находятся рекуррентно по формуле (2.67).

Все соотношения для выполнения вычислений получены. Тогда можно провести расчеты по методу Гаусса, используя прямой и обратный ход.

Покажем, что изложенный метод аппроксимации краевых условий, содержащих производные по пространственным переменным, не только повышает порядок аппроксимации, но и сохраняет консервативность конечно-разностной схемы, т. е. в конечно-разностной аппроксимации соблюдаются законы сохранения, на основе которых выведены дифференциальные соотношения задачи (2.54)-(2.57). Для этого рассмотрим вначале вывод дифференциального уравнения теплопроводности (2.54) в случае b = с = 0 (см. рис. 2.3 а).

Рис. 2.3 - К аппроксимации краевых условий, содержащих производные, с сохранением консервативности

Из физики известно, что тепловой поток, согласно закону Фурье, в одномерном случае равен , где- коэффициент теплопроводности. Для элемента длиной, в центре которого помещен узел xj, запишем сумму тепловых потоков:, подходящих к левой и правой границам элемента. По закону сохранения энергии сумма этих тепловых потоков равна изменению энергии в этом элементе, которая пропорциональна массе элемента, теплоемкости материала с и производной первого порядка от температурыпо времени

.

Разделив это равенство на и перейдя к пределу при, получим одномерное уравнение теплопроводности

, .

Таким образом, конечно-разностная аппроксимация (2.58) дифференциального уравнения (2.54) учитывает и тепловые потоки, и энергию, поглощенную элементом , т. е. все виды энергии, участвующие при выводе дифференциального уравнения.

Рассмотрим теперь вывод граничного условия (2.55) на левой границе (см. рис. 2.3 б) расчетной области (для правой границы х = l вывод аналогичен).

К граничному узлу х=0 примыкает масса объемом со стороны расчетной области. При задании граничного условия 3-го рода на левой границе х=0 осуществляется теплообмен с окружающей средой по закону Ньютона:, где- температура окружающей среды, а- коэффициент теплообмена на границе х = 0, имеющей температуру, с окружающей средой, имеющей температуру. Справа к элементуподводится тепловой поток, описываемый законом Фурье. Тогда разность тепловых потоков, подводимых к половине элемента, равна энергии, пошедшей на повышение температуры элемента, пропорциональной массе этого элемента, теплоемкости с и производной температуры по времени:

. (2.70)

Переходя здесь к пределу при , получим левое граничное условие 3-го рода (2.55) (с точностью до коэффициентов)

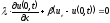. (2.71)

Таким образом, конечно-разностная аппроксимация граничного условия (2.71) или (2.55) должна сопровождаться появлением консервативного слагаемого, стоящего в правой части равенства (2.71). Физически это означает, что граничные условия (2.55), (2.56) записаны для границ, не имеющих ни массы, ни объема. В конечно-разностной аппроксимации к границе примыкает масса с одномерным объемом, равным , в котором необходимо учитывать дифференциальное уравнение, действующее во внутренних точках расчетной области, и не действующее на границе.

В конечно-разностной аппроксимации краевого условия, содержащего производную по переменной х, нестационарный член в правой части выражения (2.71) с помощью дифференциального уравнения можно заменить на дивергентный член, пропорциональный .

Аналогичный подход можно осуществить в краевых задачах для дифференциальных уравнений любых типов.