Петраков С.Н. Механизмы планирования в активных системах - неманипулируемость и множества диктаторства. М., 2001. 135 с

через r . Вектор точек пиков для профиля предпочтений ϕ ÎGSPn будем записывать как r = peak (ϕ) .

В прямых механизмах элементы сообщают оценку положения

своих точек

пиков

из

R1 ,

таким

образом, в

прямых

механизмах

множество

возможных

сообщений каждого

элемента

есть

R1 .

Пусть

элементы

посылают

в

центр

сообщения

~

1

. План

i-го элемента

ri

Î R

определяется

процедурой планирования

~

где

~

~

~

n

.

hi (r ) ,

r = (r1, ..., rn )Î R

Обозначим

вектор

планов

через

x = (x , ..., x

n

) Î Rn .

Механизм

1

планирования будет определяться множеством возможных сообщений

Rn и процедурой планирования h : Rn ® Rn .

В непрямых механизмах планирования множества возможных

сообщений	каждого		АЭ	i I	представляют		собой		отрезки
действительной оси.			Без ограничения		общности будем			считать, что
Si = [0,1] .	Таким	образом,		процедура		планирования		в	непрямом
механизме представляет собой отображение g : S ® Rn .
Как отмечалось ранее, будем рассматривать такие механизмы, в
которых каждый		АЭ	сообщает только			свою точку	пика		r Î R1 , и,
									i

следовательно, множество возможных сообщений всех АЭ – все Rn , при

этом процедура планирования будет отображением h : Rn ® Rn . Под

достоверной информацией будем понимать реальное положение точек пиков элементов. Прямой механизм планирования называется неманипулируемым, если для любых идеальных точек АЭ сообщение

достоверной информации является равновесием в доминантных

стратегиях, то есть "ϕ ÎGSPn , r = peak(ϕ)

и "iÎI, " r Î R1

, "

r

Î Rn−1

выполнено

i

−i

ϕi (hi (ri ,

i )) ³ ϕi (hi (

,

r-

ri

r−i )) .

Таким образом, первой задачей настоящего исследования можно

считать поиск условий на прямые механизмы вида

h : Rn ® Rn ,

являющиеся достаточными для его неманипулируемости.

Пусть механизм

g : S ® Rn не является прямым и для каждого

профиля

предпочтений

ϕ ÎÂ Í SPn

мы

знаем одно из положений

равновесия s (ϕ)

которое

зависит только

от

положения

точек

пиков

элементов

r Rn .

Такие

равновесия

будем

записывать

следующим

образом: s (r) .

51

Для непрямого механизма g : S → Rn построим соответствующий

ему прямой	механизм			следующим			образом.	Элементы	сообщают
информацию	~	1	, i I		о своих точках пика, центр по ним находит
	ri R
вектор равновесных заявок					s (r)	для механизма		g : S → Rn	и назначает
планы x = g(s (r)) .			Получим новый				механизм	h(r) = g(s (r)) .			Если
соответствующий		прямой			механизм		h(r) неманипулируем,			то	для
непрямого механизма				g : S → Rn		существует эквивалентный				прямой

механизм h(r) = g(s (r)) .

Таким образом, второй задачей настоящего исследования является поиск условий на исходный непрямой механизм G = (S, g) ,

являющихся достаточными для того, чтобы положение равновесия зависело только от точек пика АЭ, и соответствующий прямой механизм был неманипулируем.

Так как условия существования эквивалентного прямого механизма накладываются на исходный непрямой механизм, то

появляется возможность исследовать влияние изменений исходного непрямого механизма на существование эквивалентного прямого механизма. Поскольку менять процедуру планирования обычно не представляется возможным, актуальной является третья задача - задача

анализа влияния множества допустимых сообщений на существование эквивалентного прямого механизма.

Как было показано в обзоре, приведенном в §§ 1-5 настоящей главы, существует множество подходов к исследованию неманипулируемости. В то же время, достаточно перспективным, с точки

зрения получения условий неманипулируемости механизмов планирования, выглядит подход, предложенный в [7,94-96], который развивается в настоящей работе.

Таким образом, изучение условий неманипулируемости механизмов планирования можно свести к следующим задачам:

-получение условий неманипулируемости прямых

механизмов;

-получение условий существования эквивалентных прямых

механизмов;

-исследование влияния множества допустимых сообщений на существование эквивалентного прямого механизма.

Решение этих задач приводится соответственно в главах II и III.

52

Глава II. Условия неманипулируемости прямых механизмов планирования, сформулированные в терминах множеств диктаторства

Впредыдущей главе мы рассмотрели постановку задачи поиска неманипулируемого механизма планирования и основные проблемы, возникающие при исследовании неманипулируемости. При анализе

манипулируемости механизмов планирования будем исследовать их множества диктаторства, определяемые ниже.

Впервом параграфе приведены основные определения,

необходимые для исследования множеств диктаторства прямых механизмов планирования и достаточные условия неманипулируемости прямых механизмов планирования в терминах множеств диктаторства. Во

втором параграфе приведены необходимые и достаточные условия коалиционной неманипулируемости прямых механизмов планирования. В

§3 исследуется неманипулируемость механизмов с векторными планами.

В четвертом параграфе приводятся свойства механизмов активной экспертизы и распределения ресурса, описанных в главе I, с точки зрения метода исследования множеств диктаторства.

§1. Множества диктаторства и неманипулируемость прямых механизмов

Рассмотрим прямой механизм h : Rn → Rn . Пусть для некоторого

сообщения	~	R	n	~
	r			выбирается вектор планов x = h(r ) . Так как

полезность каждого АЭ определяется однопиковой функцией полезности,

то каждый АЭ может находиться в	одном	и только		одном из трех
~	~
возможных состояний: (а) либо hi (r ) > ri и тогда АЭ будет получать план,
строго больший желаемого, (б) либо	~	~
	hi (r ) = ri и АЭ будет назначаться
оптимальный для него план, (в)	либо	~	~	и план	будет
		hi (r ) < ri
недостаточным. Для каждого активного элемента			i I	введем	индекс

состояния, принимающий значения из набора {a, c, m}= , где a соответствует состоянию (а), с—состоянию (б), а m—(в), и обозначим его через ρi (символы индекса являются первыми буквами фр. слов

manque—нехватка, contentement—удовлетворенность, abondance—

избыток). Вектор индексов состояния всех АЭ обозначим через ρn. Введем соответствия M:n→2I, C:n→2I, A:n→2I, значениями

которых для каждого вектора состояний ρn будет подмножество АЭ из I, таких, что индексы состояний этих элементов равны, соответственно, m,

53

c и a: M(ρ)={jÎI: ρj=m}, C(ρ)={jÎI: ρj=c}, A(ρ)={jÎI: ρj=a}, ρÎ n.

Очевидно,

для

каждого

ρ

подмножества

C(ρ), A(ρ), M (ρ)

в

совокупности являются разбиением множества всех элементов I .

Определение 2.1.1. Разбиением B пространства Rn

назовем совокупность

множеств DρÍRn, таких, что

~

Î R

n

~

~

~

~

Dρ ={r

hi (r ) < ri

если i ÎM (ρ), hi (r ) = ri если i ÎC(ρ)

~

~

n

~

и hi (r ) > ri , если i Î A(

ρ)} , ρ ÎÃ .

Сокращенно

неравенства

~

при iÎM(ρ)

будем

записывать

hi (r ) < ri ,

~ ~

~

~

~

~

ρ) .

hM (ρ ) (r ) > rM (ρ)

, а неравенства hi (r ) > ri , при iÎA(ρ) как hA(ρ ) (r )

> rA(

Как видно из определения, для каждого множества

Dρ

разбиения B

задано множество элементов

C(ρ) , называемых диктаторами, которые

получают оптимальные планы, остальные элементы при этом получают некоторые неоптимальные для себя планы. Разбиение B назовем разбиением на множества диктаторства, а сами множества Dρ -

множествами диктаторства.

Далее будем предполагать, что в каждом из множеств Dρ разбиения B планы, назначаемые всем активным элементам зависят только от сообщений диктаторов C(ρ) в этом множестве и не зависит от

~

находится в

сообщений остальных элементов, если вектор сообщений r

этом множестве. То есть, существует функция x

ρ

~

(rC (ρ ) ) , определенная на

для

всех

~

такая,

что для

~

выполняется

rC (ρ ) Î ProjC(ρ) Dρ ,

всех r Î Dρ

~

ρ

~

h(r ) = x

(rC(ρ ) ) и выполнено предположение

А.2.1.1.

Для

всех

ρÎ n

существует

функция

x

ρ

: ProjC (ρ )Dρ ® R

n

~

~

ρ

~

, такая, что "r Î Dρ выполнено h(r ) = x

(rC(ρ ) ) .

Содержательно предположение А.2.1.1 означает, что планы,

назначаемые для всех векторов сообщений из одного и того же множества диктаторства, не зависят от сообщений АЭ, не являющихся диктаторами. Предположение А.2.1.1 будем считать выполненным, если не оговорено особо, в ходе всего последующего изложения.

Введенные определения иллюстрируются следующим примером.

			Пример 2.1.1. Для механизма g1(s) = s1 + 2 × s2 , g2 (s) = s1 + s2 ,
s	i	Î[0,1], i = 1, 2 ,			(r , r ) Î R2	рассмотрим соответствующий прямой
					1 2
механизм. Он задается следующими соотношениями:
x(c, c) (r , r ) = (r , r ) , при
		1	2	1	2

54

(r1, r2 ) Î D(c, c) = {(r1, r2 ) : 2×r2 -1 £ r1 £ 2×r2 , r1 -1£ r2 £ r1};
x(c, m) (r ) = (r , r ) , при (r , r ) Î D				= { (r , r ) : r Î[0,1],	r	< r 2 };
1	1 1	1 2	(c, m)	1 2 1	2	1

x(c, a) (r1) = (r1, r1 -1) , при (r1, r2 ) Î D(c, a) = { r1 [2, 3], r2 > (r1 +1)2 };

x(m, c) (r ) = (1- 2×r , r ) , при (r , r ) Î D

= { r

Î[1, 2] ,

r > 1+ r };

2

2 2

1 2

(m, c)

2

1

2

x(a, c) (r ) = (2×r , r ) , при (r , r ) Î D

= { r

Î[0,1] ,

r < r };

1

2 2

1 2

(a, c)

2

1

2

x(m, m)

= (3, 2) , при (r , r ) Î D

= { r

> 3, r > 2 };

1

2

(m, m)

1

2

x(m, a)

= (1,1) , при (r , r )Î D

= {r

> 2, r

< 1}U{r Î (1, 2], r

< 2×r } ;

1 2

(m, a)

1

2

1

2

1

x(a, m)

= (2,1) , при (r , r ) Î D

= {r

< 1, r

> 1} U{r

Î[1, 2), r

> 2 × r

-1} ;

1

2

(a, m)

1

2

1

2

1

x(a, a) = (0, 0) , при (r , r ) Î D

= { r < 0, r

< 0 }.

1

2

(a, a)

1

2

Легко проверить, что

U

D

= R2 и "ρ1 ¹ ρ2 , D

ρ

1 I D

ρ

2 = Æ , то есть B

ρ2

ρ

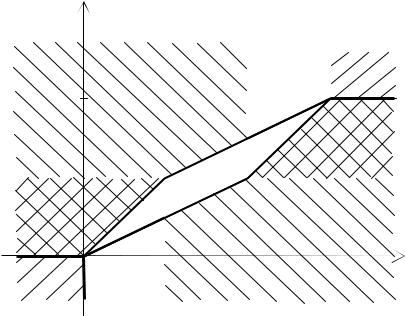
есть разбиение R2 . Множества разбиения изображены на рис. 2.1.•

Определение 2.1.2. Определим совокупность множеств

D0 ={rÎRn: rM(

)> xρ

(r

) ,

r

= Proj C(

)

D ,

rA(

)< xρ

(r

) },

ρ

ρ

M (ρ)

C(ρ)

C(ρ)

ρ

ρ

ρ

A(ρ)

C (ρ)

ρÎ n.

ρ n

Из определения 2.1.2 очевидно,

что

для

любого

выполнено включение Dρ Dρ0 . Так же очевидно,

что если для любого

вектора

сообщений

~

0

выполняется

~

ρ

~

то

для

r

Dρ

h(r ) = x

(rC(ρ ) ) ,

любого вектора истинных точек пика r Dρ0 сообщение достоверной

информации является наилучшим сообщением из Dρ0 для всех АЭ. Пример 2.1.2. Для примера 2.1.1 множества совокупности

B0 имеют вид:

D(0a, a) = {r R2 : r1 < 0, r2 < 0} ;

D0	= {r R2 : r [0, 1], x		2	< x };
(c, a)	1			1
D0	= {r R2 : r > 1, r < 1} ;
(m, a)	1	2
D0	= {r R2 : r	[1, 2], r		> 1− 2r };
(m, c)	2		1	2

55

D0

= {r R2 : r > 3, r > 2} ;

(m, m)

1

2

D0

= {r R

2 : r [2, 3], r

> 1+ r };

(c, m)

1

2

2

D0

= {r R

2 : r < 2, r > 1} ;

(a, m)

1

2

D0

= {r R2 : r [0, 1], r

< 2r } ;

(a, c)

2

1

2

D0

= D

по определению.

(c, c)

(c, c)

ножества D0

, D0

, D0

, D0

,

D0

изображены

на рис.

(a, a)

(c, a)

(m, a)

(m, c)

(m, m)

2.2.•

r

2

D(a, m)

D(c, m)

D(m, m)

D(m, c)

1

D(c, c)

D(a, c)

D0

(m, a)

1

2

3

r

0

D(c, a)

D(c, a)

Рис. 2.1. Множества B - разбиения для примера 2.1.1

Свойства множеств из B0

иллюстрируются следующей леммой.

Лемма 2.1.1. Рассмотрим произвольный r Dρ0 , тогда:

~

0

~

ρ

(2.1.1)

a) i M(ρ) { (ri

,r−i ) Dρ } {ri

> xi (rC(ρ) ) },

56

r

D(c, m)

D0

D(a, m)

(m, m)

2

D0

(m, c)

1

D(a, c)

0

D(0c, a)

D(m, a)

r

1

2

3

D(0c, a) 0

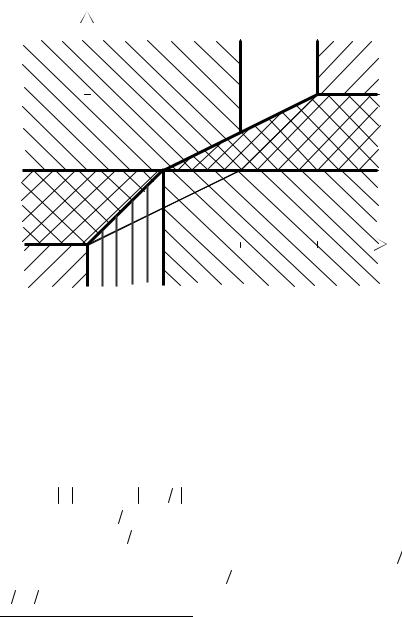
Рис. 2.2. Множества совокупности B0 для примера 2.1.2

~

0

~

ρ

2)

(2.1.2)

б) i R(ρ) {(ri ,r−i ) Dρ }

{ri < xi (rC(ρ ) )} . Þ

Под записью B=B0 будем подразумевать, что ρ n, Dρ = Dρ0 .

Теорема

2.1.1.

Пусть

I

- множество

активных

элементов,

функции полезности которых обобщенно однопиковые. Пусть механизм

h : Rn → Rn

удолетворяет А.2.1.1 и B=B0 , тогда он неманипулируем. Þ

Очевидно, условия теоремы 2.1.1 не выполнены в примере 2.1.1.

Механизм примера 2.1.1 оказывается манипулируемым. Возьмем,

например,

такой

профиль

предпочтений,

что

функции

полезности

ϕ1(x1) = − x1 ,ϕ2 (x2 ) = − x2 −1 2

имеют

точки

пика

равные

соответственно (0,1 2) . Сообщая достоверную информацию,

элементы

получают планы

(1,1 2)

и полезности (1, 0)

соответственно.

Если же

первый активный элемент сообщит недостоверную информацию:

1 2 , а

второй сохранит

своё

сообщение

1 2 , то

будут

назначены

планы

(1 2,1 2) и полезности элементов в этом случае будут (0, 0) .

2) Символ “ Þ ” после формального утверждения означает, что его

доказательство приведено в приложении

57

Таким образом, в настоящем разделе сформулированы

достаточные условия неманипулируемости прямых механизмов планирования, накладывающие ограничения на структуру множеств диктаторства (Т.2.1.1). Кроме этого, исследование манипулируемости механизмов планирования в АС с двумя АЭ (примеры 2.1.1, 2.1.2) дает

наглядную геометрическую интерпретацию условий неманипулируемости в терминах множеств диктаторства.

58

§2. Коалиционная неманипулируемость прямых механизмов

В §1 настоящей главы были построены достаточные условия неманипулируемости прямых механизмов планирования. В настоящем

параграфе мы введем понятие коалиционной неманипулируемости и получим необходимые и достаточные условия коалиционной неманипулируемости для механизмов, удовлетворяющих предположению А.2.1.1.

Введем несколько отношений между векторами в

Rn ,

которые

будут необходимы

нам

в

дальнейшем.

Будем

писать,

что

x < ρ > y ,

x, y Î Rn если

x

= y

ρ )

, x

A(ρ)

< y

A(ρ )

,

x

M (ρ )

> y

M (ρ )

.

Используя это

C (ρ )

C (

обозначение, определение множеств Dρ , Dρ0

можно записать следующим

образом:

~

~

~

Dρ =

Î R

n

n

{r

r

< ρ > h(r )}, ρ ÎÃ .

0

~

Î R

n

~

~

< ρ > x

ρ

~

n

Dρ

= {r

rC(ρ ) ÎProjC(ρ) Dρ , r

(rC (ρ) )},

ρ ÎÃ

Кроме отношения < ρ > определим отношение < ρ > . Будем

записывать

x <

> y , если xC (ρ ) = yC (ρ ) , xA(ρ) £ yA(ρ ), xM (ρ ) ³ yM (ρ) .

ρ

Для каждого подмножества активных элементов

J I и для

каждого вектора состояний ρ ÎÃn

определим

множества

D(ρ, J ) и

вектора состояний c(ρ, J )

следующим образом:

D

0

~

n

~

Î Proj

~

ρ

~

~

ρ

~

(ρ, J ) = {r Î R

rC (ρ)

Dρ , rJ = xJ

(rC(

ρ) ), r− J

< ρ > x−J

(rC(ρ ) )} ,

C (ρ)

c(ρ, J )ÎÃn : c

J

(ρ, J ) = ρ

J

и "i Î I \ J ® c (ρ, J ) ='c' .

i

В дальнейшем будем исследовать прямые механизмы,

удовлетворяющие следующему условию

A.2.2.1. "ρ ÎÃn, "J Î I ® D0(ρ, J ) Í Dc0(ρ, J ) .

Условие А.2.2.1 содержательно означает, что при переходе из множества диктаторства Dρ , ρ ÎÃn с меньшим числом диктаторов в

множество Dc(ρ, J ) с большим количеством диктаторов, АЭ не являвшиеся диктаторами в Dρ получат планы, не лучшие прежних.

59

Будем говорить, что прямой механизм						h : Rn ® Rn коалиционно
	если r R	n		~		J
манипулируем,			,	J I , $rJ Î R			такие, что j J →
~	)) ³ ϕ j (hj (rJ , r−J						~
® ϕ j (hj (rJ , r−J				)) и $i Î J ® ϕi (hi (rJ , r−J )) > ϕi (hi (rJ , r−J )) .

Содержательно, это означает, что при некотором профиле предпочтений найдется коалиция элементов, каждый элемент которой не

проигрывает от сообщения недостоверной информации и найдется элемент, который строго выигрывает.

Следует отметить, что такое определение коалиционной неманипулируемости расходится с общепринятым [22,108]

Определение 2.2.1. Коалиционно неманипулируемым назовем

n

n

r R

n

~

J

механизм h : R

~

® R

такой, что

,

J I ,

"rJ Î R

→

)) £ ϕi (hi (rJ , r−J ))}

или

{$j Î J :

{i J → ϕi (hi (rJ , r−J

ϕ j (hj (~rJ , r−J )) < ϕ j (hj (rJ , r− J ))} .

Коалиционная неманипулируемость означает, что для любого

профиля предпочтений и для любой коалиции ни какая коалиция АЭ не может получить выигрыш от создания коалиции либо полезность одиного из АЭ рассматриваемой коалиции строго убывает при образовании коалиции.

Верны следующие утверждения

Лемма 2.2.1. Пусть механизм h : Rn ® Rn удовлетворяет

предположениям А.2.1.1, А.2.2.1 и для него D = D0 , тогда этот механизм коалиционно неманипулируем. Þ

Лемма 2.2.2. Пусть механизм h : Rn ® Rn удовлетворяет А.2.1.1 и коалиционно неманипулируем, тогда D = D0 . Þ

Лемма 2.2.3. Пусть механизм h : Rn ® Rn удовлетворяет А.2.1.1 и коалиционно неманипулируем, тогда выполнено А.2.2.1. Þ

Следствием Л.2.2.1-Л.2.2.3 является следующая теорема. Теорема 2.2.1. Для того, чтобы прямой механизм h : Rn ® Rn

удовлетворяющий А.2.1.1, был коалиционно неманипулируем необходимо и достаточно, чтобы выполнялись условия А.2.2.1 и

D = D0 . Þ

Теорема 2.2.1 дает необходимые и достаточные условия для

коалиционной неманипулируемости прямых механизмов в смысле определения 2.2.1.

Вследующем параграфе мы рассмотрим обобщения результатов

§1 настоящей главы на механизмы планирования с векторными планами,

60