Петраков С.Н. Механизмы планирования в активных системах - неманипулируемость и множества диктаторства. М., 2001. 135 с

Глава III. Существование эквивалентных прямых механизмов

При построении механизмов функционирования АС центр может иметь некоторый исходный механизм планирования, в котором сообщение достоверной информации не является равновесием. В таком

случае центр может попытаться определить для каждого возможного профиля предпочтений одно из равновесий Нэша и на его основе построить соответствующий исходному прямой механизм. В настоящей главе приводятся условия, гарантирующие существование эквивалентных

прямых механизмов для непрямых механизмов планирования и конструктивно определяется вид эквивалентного прямого механизма.

В § 1 настоящей главы определяется формализм метода множеств диктаторства по отношению к непрямым механизмам. В § 2 приводятся условия существования равновесия Нэша. В § 3 приводятся общие условия существования эквивалентных прямых механизмов, на основании которых в § 4 строятся конструктивные условия существования

эквивалентных прямых механизмов для линейных и дифференцируемых механизмов планирования.

§1. Прямые и непрямые механизмы планирования

Пусть механизм g : S → Rn не является прямым и для каждого

профиля предпочтений ϕ SPn			мы знаем одно из	положений
равновесия	s (ϕ)	которое зависит только от положения		точек пиков
элементов	r Rn .	Такие равновесия	будем записывать	следующим

образом: s (r) .

Для непрямого механизма g : S → Rn построим соответствующий

~	R	1	, i I	о
ему прямой механизм. Элементы сообщают информацию ri

своих точках пика, центр по ним находит вектор равновесных заявок s (r) для механизма g : S → Rn и назначает планы x = g(s (r)) . Получим новый механизм h(r) = g(s (r)) . Если соответствующий прямой

механизм	h(r) удовлетворяет условиям теоремы	2.1.1, то		он
неманипулируем и, следовательно, для непрямого механизма			g : S → Rn
существует	эквивалентный прямой механизм (см.	§ 1	главы	I)
h(r) = g(s (r)) .

71

В настоящей главе			будем рассматривать непрямые механизмы
следующего	вида.	Пусть	планы	элементам назначаются по заявкам
si Si = [0,1]	в	соответствии		с	процедурой	планирования
x = g(s), x Rn , s = (s1, ..., sn) S = [0,1]n .					Будем предполагать, что
процедура планирования непрерывна в S					и частично монотонна, то есть
gi (s) не убывает по si при любых s S .

В настоящей главе мы получим условия на механизм g : S → Rn ,

которые достаточны для того, чтобы соответствующий прямой механизм h(r) удовлетворял теореме 2.1.1, которая гарантирует его

неманипулируемость.

Для того, чтобы получить такие условия существования эквивалентного прямого механизма, для каждого возможного профиля предпочтений необходимо найти хотя бы одно равновесное сообщение.

Поэтому в следующем параграфе мы докажем теорему о существовании равновесия Нэша для непрямых механизмов планирования.

72

§2. Существование равновесия Нэша
Рассмотрим		непрямой механизм	g :[0, 1]n ® Rn .		Пусть	для
некоторого	r Î Rn	существует положение равновесия		s (r) . При этом
данному r	можно сопоставить вектор		состояний	ρ	такой,	что

gC(ρ ) (s (r)) = rC(ρ) , gM (ρ ) (s (r)) < rM (ρ ) , gA(ρ ) (s (r)) > rA(ρ) . В силу того,

что s (r) - равновесие Нэша,				элементы i Î M (ρ) будут сообщать заявки
si Î Arg max gi (si¢,s−i ) , элементы					i Î A(ρ) , si Î Arg min gi (si¢, s−i )		и
		si′[0,1]				si′[0,1]
si Î[0,1] , i ÎC(A) .						{si =1}Î Arg max gi (si′, s−i )
		В силу частичной монотонности					и
						si′[0,1]
{si = 0}Î Arg min gi (si′,s−i ) .				Далее	будет	доказано, что в равновесии
		si′[0,1]
s = 1, i Î M (A) ;			s = 0, i Î A(A) и s Î[0,1], i ÎC(A) .
	i		i	i
		Найдем положения равновесия для механизма примера 2.1.1.
		Пример 3.2.1. Для механизма g1(s) = s1 + 2 × s2 , g2 (s) = s1 + s2 ,
s	i	Î[0,1], i = 1, 2 ,	(r , r )Î R2	найдем одно из возможных равновесий для
			1 2

всех профилей ϕ Î SPn . Очевидно для всех функций полезности с точкой

пика r Î D	вектор сообщений		s = (1,1)	будет	равновесием Нэша.
(m, m)
Действительно,	пусть r Î D	,	например	r = (4,	3) . g(s ) = (3, 2) и,
	(m, m)

изменяя свое сообщение, первый АЭ не может получить план больший

трех,

поскольку

при

g(s , s ) < 3 для

всех

s

i

Î[0,1] .

Поскольку

1 2

функция полезности

ϕ1 строго

возрастает

до

точки пика

r1 = 4 , то

ϕ (g (s )) > ϕ (g (s , s )) .

Аналогично

"s

2

Î[0,1],

1

1

1

1

1

2

ϕ

2

(g

2

(s )) > ϕ

2

(g

2

(s , s )) . Тогда

s = (1,1)

является равновесием Нэша

1

2

для всех профилей предпочтений, задаваемых однопиковыми функциями полезности таких, что их точки пика r1 = 4, r2 = 3 .

Аналогично, для любого профиля предпочтений ϕ Î SPn , такого,

что вектор	точек пиков		профиля r Î D(c, m) , равновесие Нэша
определяется	выражением		s (r) = (r - 2,1) . Например,	для профиля с
			1	s (r) = (0,5;1) .
точками пиков r = 2,5 и		r	= 2 . Положение равновесия
	1	2

73

Действительно, при s1 = 0,5 , s2 = 1, g1(s ) = 2,5, g2 (s ) =1,5 . Как видим

при таком векторе сообщений первый активный элемент получает максимально возможную полезность и меняя своё сообщение "s1 Î[0,1] ,

ϕ (g(s )) > ϕ

2

(g(s , s )) . Аналогично невыгодно менять своё сообщение

1

1

2

(s ) > g

(s , s

второму

элементу,

так

как

"s

2

Î[0,1) g

2

2

2

) .

Значит

s (r) = (0,5;1)

1

является равновесием Нэша при r = (2,5; 2) .

Приведем выражения для векторов равновесных сообщений, если

r Î D

,

s (r) = (1,1) ;

(m, m)

r Î D

,

s (r) = (1, r

-1) ;

(m, c)

2

r Î D

,

s (r) = (1, 0) ;

(m, a)

r Î D

, s (r) = (r ,1) ;

(c, a)

1

r Î D

,

s (r) = (0, 0) ;

(a, a)

r Î D

,

s (r) = (0, r ) ;

(a, c)

2

r Î D

,

s (r) = (0,1) ;

(a, m)

r Î D

, s (r) = (r - 2,1) .●

(c, m)

1

В записи s−J

индекс " −J ", где

J - подмножество I , обозначает

по аналогии с индексом " −i " все компоненты вектора

s ,

которые не

принадлежат J .

s−ρC(ρ )

Для каждого вектора

состояний

ρ ÎÃn

определим вектор

размерности

I \ C(ρ)

, с компонентами sρ , i Î I \ C(ρ) :

i

ì0, i Î A(ρ);

siρ = í

î1, i Î M (ρ).

Так же, для каждого вектора состояний определим множества

Sρ = {s Î Rn : sM (ρ ) > sMρ (ρ) , sA(ρ ) < s

Для случая двух элементов, разбиение {Sρ }

ρ		C(ρ )		n
A(ρ ) , sC(ρ) Î[0,1]				}, ρ ÎÃ .

изображено на рис. 3.1.

Далее нам потребуется некоторые очевидные из геометрических соображений свойства множеств Sρ , ρ ÎÃn , доказательства которых приводятся в приложении.

74

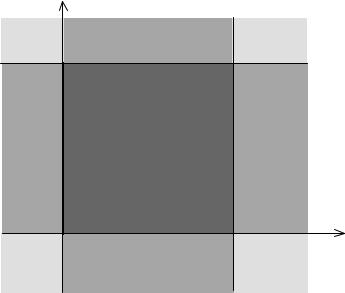
Утверждение 3.2.1. Совокупность множеств {Sρ }ρn							есть разбиение
Rn . Þ
Следующим утверждением устанавливается свойство малых
окрестностей точек в Rn по отношению к разбиению							{Sρ }ρn :		для
каждой точки s Î Rn		существует набор
		s 2
	S ( c , m )		S ( c , m )			S ( m , m )
		1
	S ( a , c )		S ( c , c )			S ( m , c )
		0			1			s1
	S ( a , a )		S ( c , a )			S ( m , a )
			Рис. 3.1
множеств разбиения {Sρ }ρn , определяемый множеством их векторов
состояний Ã0 (s) такой, что все достаточно малые окрестности точки s
пересекаются только с множествами Sρ , ρ ÎÃ0 (s) .
Утверждение 3.2.2. Для любого					s Î Rn	существует множество
векторов	состояний	0		и	число	ε0 > 0		такие,	что
"ε Î(0, ε0 ), "ρ ÎÃ0 ,Uε (s) I Sρ			¹ Æ и "ρ ÏÃ0,Uε (s) I Sρ ¹ Æ . Þ
									75

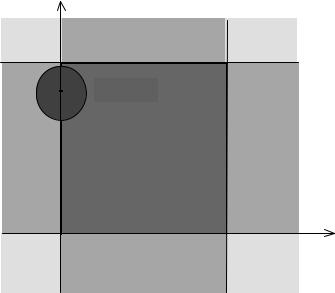
Пример 3.2.2. Поясним это утверждение на следующем примере
(см. рис. 3.2). Рассмотрим точку s Î R2 , s = (0, 0,9)					и окрестность радиуса
1,5 . Эта окрестность будет пересекаться со всеми множествами разбиения
{Sρ }ρn . Окрестность радиуса 1 будет пересекаться только со
множествами S(a, a), S(c, a), S(a, c), S(c, c) , S(a, m), S(c, m) .					Окрестность радиуса
0,5 будет пересекать только множества S(a, c) , S(c, c), S(a, m) , S(c, m) .							А все
окрестности радиуса меньше 0,1 пересекаются только с двумя
множествами	S(a, c), S(c, c) . Поэтому множество Ã0				для точки s = (0, 0,9)
будет состоять из элементов Ã0 = {(a, c), (c, c)}.●
Далее докажем, что любой отрезок с началом не						в	S(c, ..., c)
пересекается	с	внутренностью	некоторого	множества		Sρ ,		где
ρ ¹ {c,..., c} .
		s 2
S ( c , m )		S (c , m )			S ( m , m )
		1
		s = (0, 0,9)
S ( a , c )		S ( c , c )			S ( m , c )
		0		1		1
S ( a , a )		S (c , a )			S ( m , a )
		Рис. 3.2
76

Утверждение

3.2.3.

Пусть

s1 ¹ s2 Î Rn.

s1 Î Sρ1

и

s2 Î Sρ 2

ρ1 ¹ {c, ..., c} , тогда

α > 0

и

$ρ¢ÎÃ:"t Î (0,α) s(t) = s1(1- t) + s2t Î S

и ρ′ ¹ {c,..., c} . Þ

Определим множества Q

ρ

= {s Î Rn : s

Î R

C(ρ )

, s

−C (ρ)

= sρ

}

C (ρ )

−C (ρ )

и

ρ′

и

произвольные

s1, s2 Î Rn

такие, что

они принадлежат разным

множествам разбиения {Sρ }, то есть можно указать такие вектора ρ1, ρ 2 ,

ρ1 ¹ ρ2 что s1 Î Sρ1

и s2 Î Sρ 2 .

Рассмотрим

отрезок

[s1, s2 ] = {s(t) = s1t + s2 (1- t), t Î[0,1]}. При

ρ = {c,..., c} ,

[s

1

, s

2

] Ì Qρ = R

n

~

. Найдем множество Ã всех векторов из

n

таких,

что

1

2

] Ì Qρ ,

~

Обозначим

Ã

[s , s

ρ ÎÃ.

¢

1

2

) = Argmax

I \ C(ρ)

.

Ã

(s , s

~

ρ

Поясним введенные определения на следующем примере.

Пример 3.2.3. Рассмотрим разбиение {Sρ }ρn и отрезок [s1, s2 ] ,

где s1 = (-0,3,1) ,

s1 = (0,5,1) . Множества Qρ

будут следующими (см. рис.

3.3)

= R2 ;

Q

(c, c)

Q(m, m) = (1,1) ;

77

s2
S( c, m )	S ( c , m )	S ( m, m)
1
S ( a , c )	S ( c , c)	S( m, c )
0		s1
		1
S( a , a )	S( c , a )	S( m, a )
	Рис. 3.3

Q(a, m)

Q(m, a)

Q(a, a)

Q(c, a)

Q(a, c)

Q(c, m)

Q(m, c)

Тогда [s1 ,

=(0,1) ;

=(1, 0) ;

=(0, 0) ;

={r R2 : s1 (−∞, + ∞), s2 = 0} ;

={r R2 : s1 (−∞, + ∞), s2 = 1} ;

={r R2 : s2 = 0, s2 (−∞, + ∞)};

={r R2 : s1 = 1, s2 = (−∞, + ∞)} .

s2 ]

будет

принадлежать

Q(c, c)

и

Q(c, m) .

~	1	2	) = {(c, c), (c, m)} .					При	этом
(s , s
′(s1, s2 ) = Argmax					I \ C(ρ)		= {(c, m)}.●	множество ′(s1, s2 )
	Утверждение 3.2.4. s1, s2 R2								состоит из
одного элемента.

78

~

Единственный элемент ρ ÎÃ′ обозначим ρ . Þ

Поскольку для каждого s Rn

существует единственный

ρ ÎÃn

такой,

что

s Î Sρ ,

то

однозначным

будет

следующее

доопределение

отображения

g : S ® Rn

на все

Rn . Рассмотрим произвольный

s Rn ,

существует единственный ρ ÎÃn такой, что s Î Sρ . В точке s

определим

функцию

G(s)

таким

образом,

что

G

(s) = g

C(ρ )

(sρ

, s

)

и

C(ρ )

−C(ρ )

C (ρ )

G

(s) = g

−C (ρ )

(sρ

, s

) + (s

−C (ρ )

- s

ρ

) .

Очевидно,

если

−C(ρ)

−C(ρ )

C(ρ)

−C(ρ)

s Î S = [0,1]n

то G(s) = g(s) .

Пример 3.2.4. Рассмотрим доопределение функции

g : S ® Rn

для

механизма примера 2.1.1.

Если s ÎS(c, c) , то g(s) = G(s) .

Если

ρ = (c, m) , то C(ρ) = {1} и I \ C(ρ) = {2} , и s(c, m)

= s(c, m)

= 1.

При этом G(s)

−C (ρ )

2

для всех s Î S(c, m)

определится следующим образом:

æG (s) ö

æ g (s ,1) ö æ0

ö æs + 2

ö æ s + 2 ö

G(s) = ç

1

÷

=

ç 1 1

÷

+ ç

÷ = ç

1

÷ = ç

1

÷ .

èG2 (s)ø è g2 (s1,1)ø è s2 -1ø ès1 +1+ s2 -1ø è s1 + s2 ø

Если

ρ = (c, m) ,

то

C(ρ) = Æ

и

s(m, m)

æ1ö

для всех

= ç

÷ , а G(s)

è1ø

s S(m, m)

определится следующим образом:

æG (s) ö

æ g

(1,1) ö

æ s

-1 ö

æs

+ 2

ö

G(s) = ç

1

÷

= ç 1

÷ + ç

1

÷ =

ç

1

÷ .

èG2 (s)ø

è g2 (1,1)ø

è s2 -

1ø

ès2 +1

ø

При s Î S(m, c) , аналогично получаем:

æG (s) ö

æ g (1, s

) ö

æ s -1ö

æ s + 2s

ö

G(s) = ç

1

÷

= ç 1

2

÷

+ ç

1

÷ = ç

1

2

÷ .

èG2 (s)ø

è g2 (1, s2 )ø

è

0

ø

è s2 +1

ø

При s Î S(m, a) ,

æG (s) ö

æs

ö

G(s) = ç

1

÷

= ç

1

÷ .

èG2 (s)ø ès2 +

1ø

При s S(c, a)

æG (s) ö

=

æ s

ö

, G(s) = ç

1

÷

ç

1

÷ .

èG2 (s)

ø è s1 + s2 ø

При s Î S(a, a) ,

æG (s) ö

=

æs

ö

G(s) = ç

1

÷

ç

1

÷ .

èG2(s)ø ès2 ø

79

При s Î S(a, c) ,

æG (s) ö æ s + 2s

ö

G(s) = ç

1

÷ = ç 1

2

÷ .

èG2 (s)ø è s2

ø

При s Î S(a, m) ,

æG (s) ö æs + 2ö

G(s) = ç

1

÷

= ç

1

÷ .•

èG2 (s)ø ès2

ø

Приведем

некоторые

свойства

функции

G ,

доказательства

которых можно найти в приложении.

Лемма 3.2.1. G (s) не убывает по s

для любых s Î Rn . Þ

i

i

Лемма 3.2.2. G(s) непрерывна в Rn . Þ

Лемма 3.2.3. Если g(s) непрерывна и частично монотонна, то для

любого r Rn существует s Î Rn

такой, что G(s) = r . Þ

Лемма 3.2.3 позволяет доказать справедливость следующего

утверждения о существовании и структуре равновесия.

g : S ® Rn

Теорема

3.2.1.

Пусть

процедура

планирования

непрерывна в S и частично монотонна в S. Тогда для любого ϕ ÎGSPn

с

вектором

точек

пиков

r Rn

существуют

равновесие

Нэша s (r)

и

вектор

состояний

ρ ÎÃn

такие,

что

s (r) = (sρ

,s

C(ρ )

) , где

−C (ρ )

s

C(ρ )

Î[0,1]

C(ρ )

. При этом g

C(ρ )

(s (r)) = r

, g

M (ρ)

(s (r)) < r

M (ρ)

и

C(ρ)

gA(ρ ) (s (r)) > rA(ρ) . Þ

Как видно из теоремы 3.1.1, положение равновесия для каждого

профиля зависит только от вектора точек пиков и не зависит от конкретного вида функций полезности.

Таким образом, мы ввели разбиение пространства Rn на множества Sρ и, используя это разбиение, доопределили процедуру

планирования g(s), s Î[0,1]n на все Rn .

Это доопределение позволило нам доказать теорему 3.2.1 о существовании и структуре равновесия Нэша в механизме (S, g) . В

дальнейшем свойства, устанавливаемые утверждениями 3.2.1-3.2.3 и теоремой 3.2.1 понадобятся при построении достаточных условий существования эквивалентного прямого механизма.

80