
- •Глава 1. Линейная алгебра.
- •§1. Матрицы и действия над ними.
- •1.1. Понятие матрицы
- •1.2. Основные операции над матрицами и их свойства.
- •§2. Определители.
- •2.1. Понятие определителя.
- •2.2. Свойства определителей.
- •§3. Обратная матрица.
- •3.1. Понятие обратной матрицы. Теорема об обратной матрице.
- •3.2. Метод элементарных преобразований.
- •§4. Системы линейных уравнений. Методы решения.
- •4.1. Понятие системы линейных уравнений.
- •4.2. Матричный способ решения слу.
- •4.3. Формулы Крамера.
- •§5. Ранг матрицы. Теорема кронекера-капелли. Решение произвольных методов гаусса. Однородные системы.
- •5.1.Ранг матрицы.
- •5.2. Методы нахождения ранга матрицы.
- •5.3. Теорема Кронекера-Капелли.
- •5.4.Решение произвольных систем методом Гаусса.
- •5.5. Однородные системы.
- •§6. Линейные и евклидовы пространства.
- •6.1. Понятия вектора, линейного пространства.
- •6.2. Линейная зависимость векторов. Базис.
- •6.3. Евклидовы пространства. Неравенство Коши-Буняковского.
§2. Определители.
2.1. Понятие определителя.
Рассмотрим произвольную квадратную матрицу порядка n
А=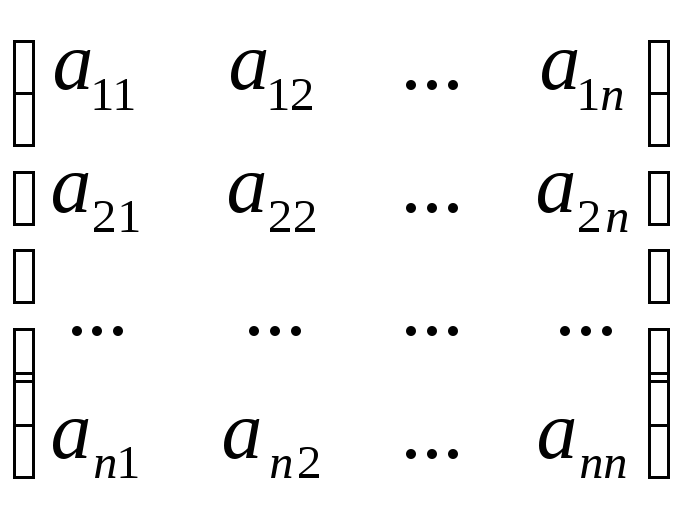
Каждой такой матрице можно поставить в соответствие числовую характеристику, называемую определителем, соответствующим этой матрице.
Обозначение ∆=detA=|A|=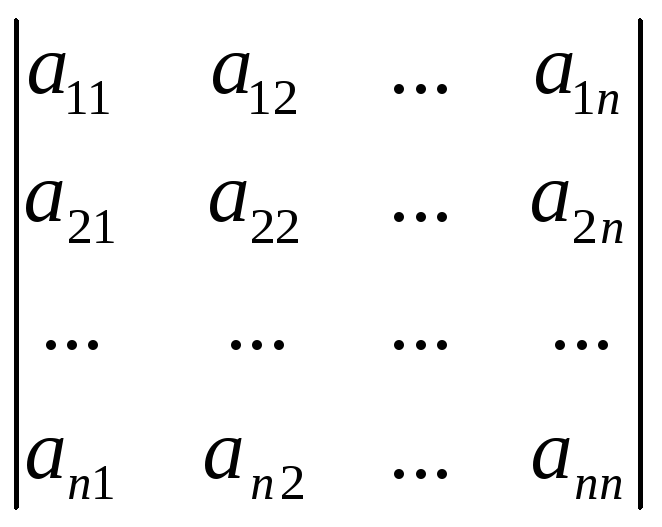 (1)
(1)
Если порядок матрицы А n=1, то есть А=(a11), то определителем первого порядка, соответствующим такой матрице, называется величина этого элемента, т.е. |A|= a11.
Если n=2, то есть матрица
А имеет видА=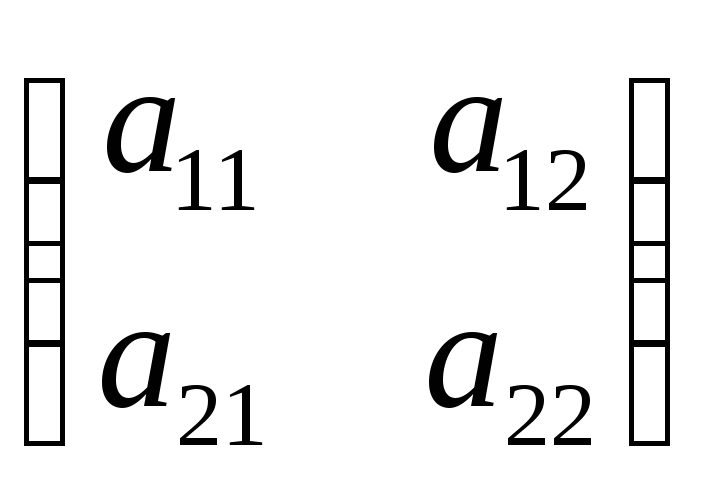 ,
то определителем второго порядка,
соответствующим такой матрице, называется
числоa11a22–a21a12,т.е. определитель второго порядка равен
разности произведения элементов, стоящих
на главной диагонали, и произведения
элементов, стоящих на побочной диагонали.
,
то определителем второго порядка,
соответствующим такой матрице, называется
числоa11a22–a21a12,т.е. определитель второго порядка равен
разности произведения элементов, стоящих
на главной диагонали, и произведения
элементов, стоящих на побочной диагонали.
Т.о. по
определению ∆=det A=|A|=![]() =
a11a22–a21a12.
=
a11a22–a21a12.
Пример: А=![]() |А|=
|А|=![]() =1·3–(–1)·2=5
=1·3–(–1)·2=5
Если n=3, то естьA= ,
то определителем 3-го порядка этой
матрицы называется число, равное
,
то определителем 3-го порядка этой
матрицы называется число, равное
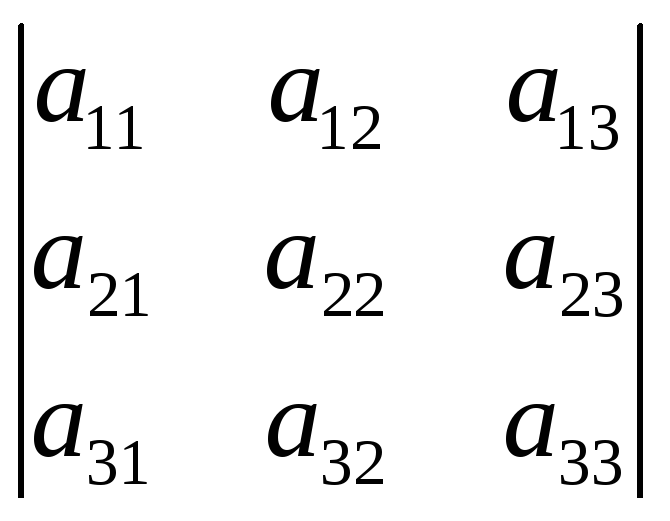 =а11а22а33+а12а23а31+а21а32а13–а31а22а13–а21а12а33–а11а23а32.(2)
=а11а22а33+а12а23а31+а21а32а13–а31а22а13–а21а12а33–а11а23а32.(2)
Правила вычисления определителей третьего порядка:
1) правило треугольника:
 =
= –
–
2). правило «дождика»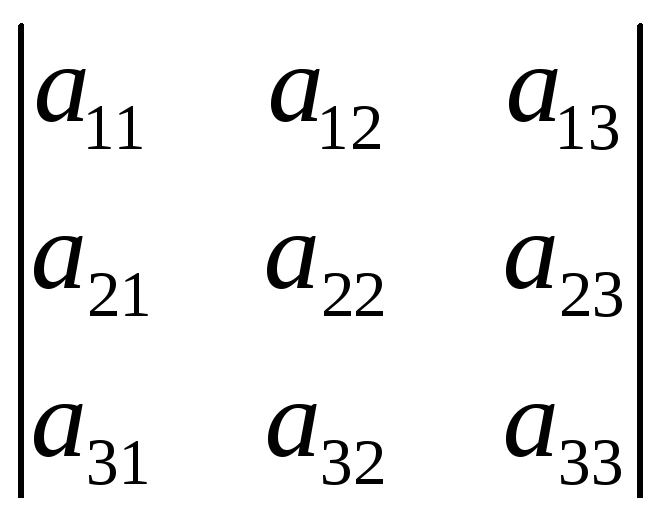
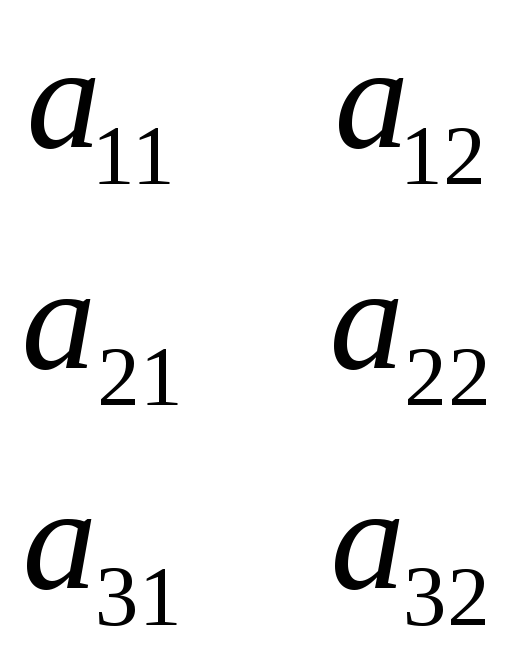
– – – + + +
Пример:
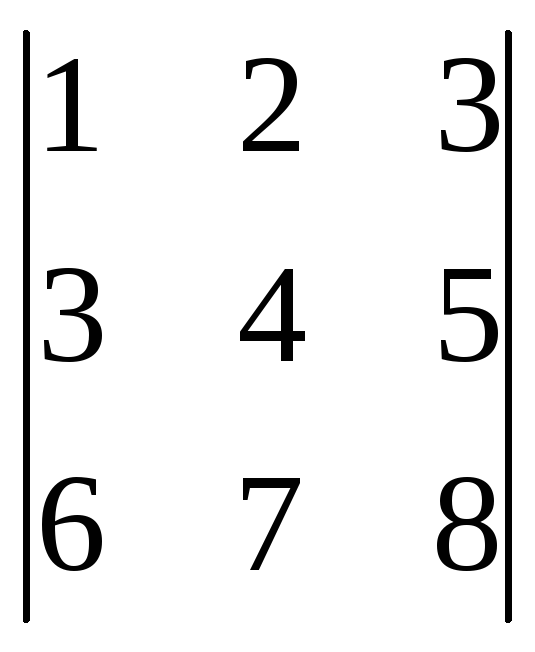 =1·4·8+2·5·6+3·3·7–6·4·3–3·2·8–1·5·7=32+60+63–72–48–35=155–155=0
=1·4·8+2·5·6+3·3·7–6·4·3–3·2·8–1·5·7=32+60+63–72–48–35=155–155=0
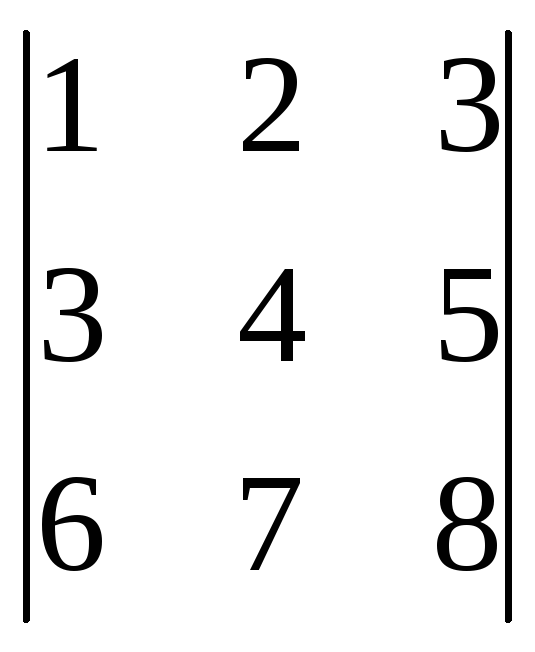
![]() =0
=0
Минором Мij некоторого элементааijопределителяn-го порядка (1) называется определитель (n–1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.
Пример: |A| =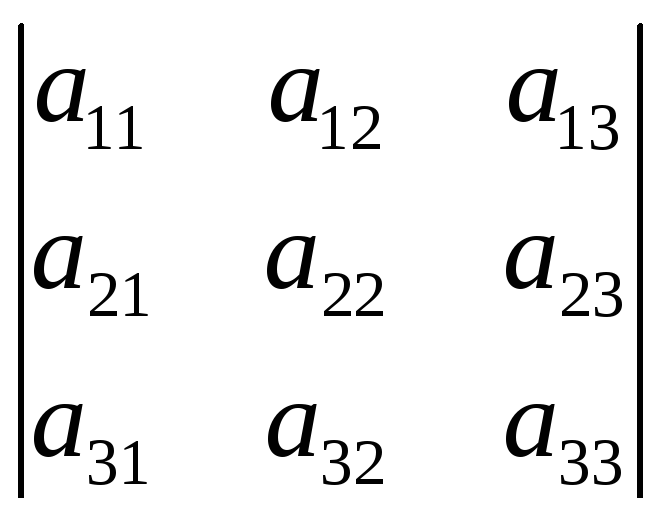 M32=
M32=![]() M21=
M21=![]()
|A| =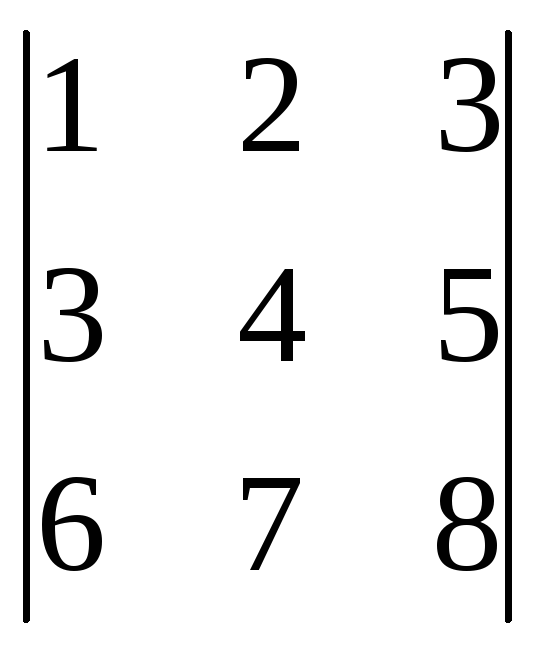 M32=
M32=![]() =5–9=–4
=5–9=–4
Алгебраическим дополнением Аijэлементааijназывается минор этого элементаМij, умноженный на (–1)i+j, т.е.Аij=(–1)i+j Мij.
Пример: |A| =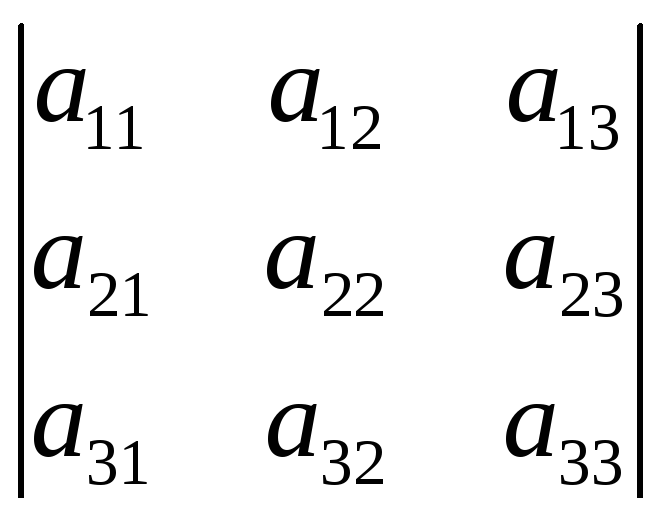 А32=(–1)3+2
А32=(–1)3+2![]() = –
= –
![]()
А21=(–1)2+1![]() = –
= –
![]() |A| =
|A| = А32=–
А32=–![]() =–(5–9)=4
=–(5–9)=4
Используя эти понятия определитель 3-го порядка можно записать следующим образом:
|A| =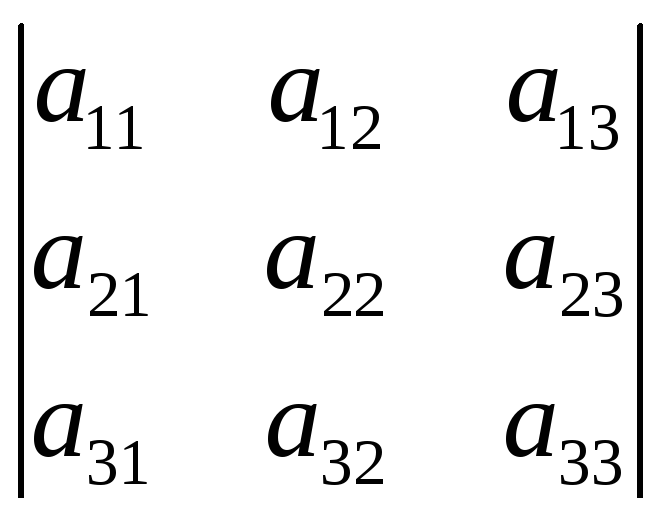 =а11А11+а12А12+а13А13– разложение определителя 3-го порядка
по 1-ой строке. Если расписать в этой
формуле каждое алгебраическое дополнение
и раскрыть скобки, то получится формула
(2).
=а11А11+а12А12+а13А13– разложение определителя 3-го порядка
по 1-ой строке. Если расписать в этой
формуле каждое алгебраическое дополнение
и раскрыть скобки, то получится формула
(2).
Задание: проверить это равенство самостоятельно.
Пример:
 = 0.
= 0.
Замечание: Разложение определителя можно проводить по любой строке или столбцу.
Определителем квадратной матрицы А=(аij)n-го порядка называется число
∆=detA=|A|=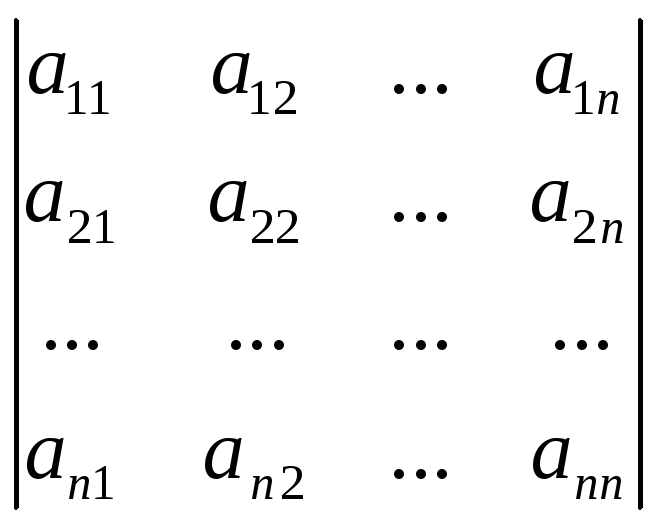 =
=![]() =
=![]()
разложение по разложение по
элементам i-й строки элементамj-го столбца
2.2. Свойства определителей.
Сформулируем и докажем эти свойства для определителей 3-го порядка. Они справедливы и для определителей любого порядка.
1. Определитель не меняется, если его строки и столбцы поменять местами. Это свойство устанавливает равноправие строк и столбцов определителя. Поэтому в дальнейшем для краткости все свойства будут сформулированы для столбцов (для строк то же самое).
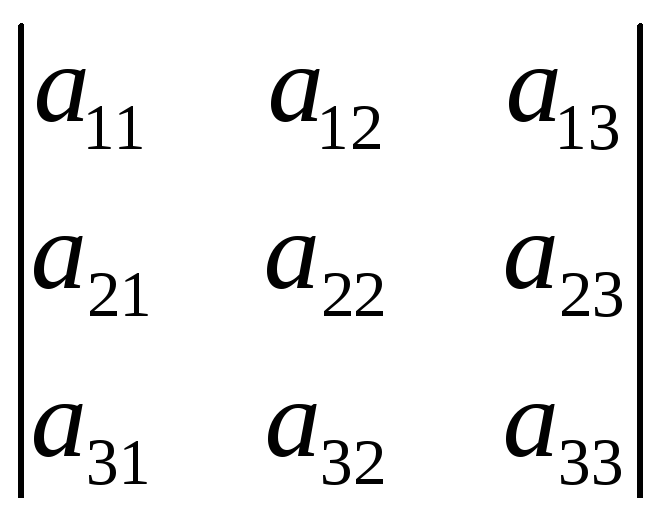 =
=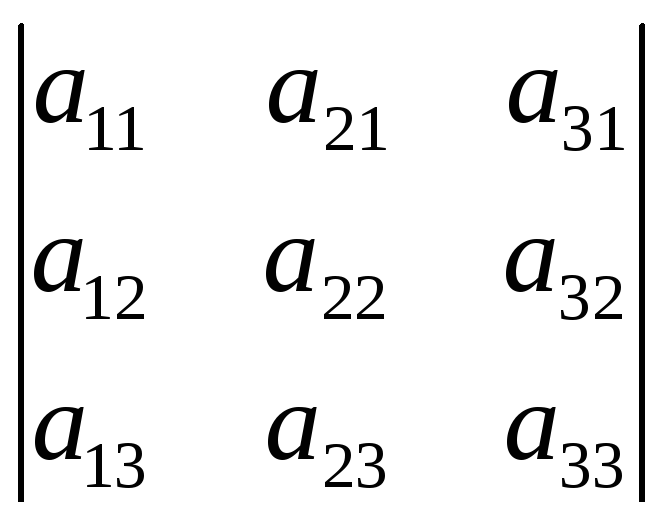 .(посчитать
левый и правый и сравнить)
.(посчитать
левый и правый и сравнить)
2. При перестановке двух столбцов местами определитель меняет знак.
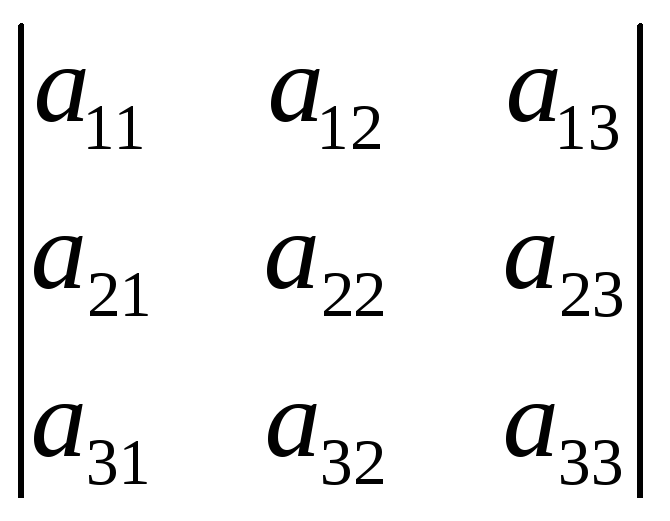 = –
= –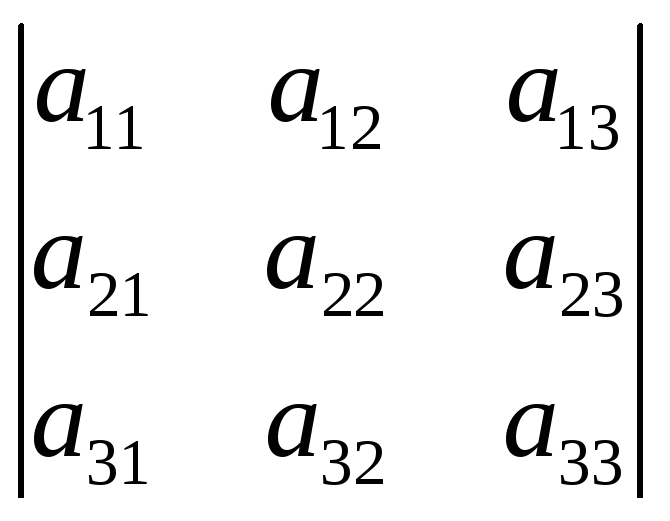 (посчитать
левый и правый и сравнить)
(посчитать
левый и правый и сравнить)
3. Определитель, содержащий два одинаковых столбца равен нулю.
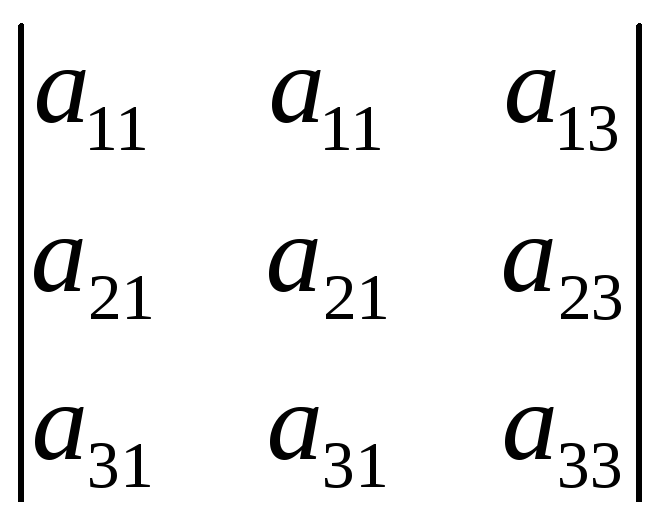 = (по второму св-ву) –
= (по второму св-ву) –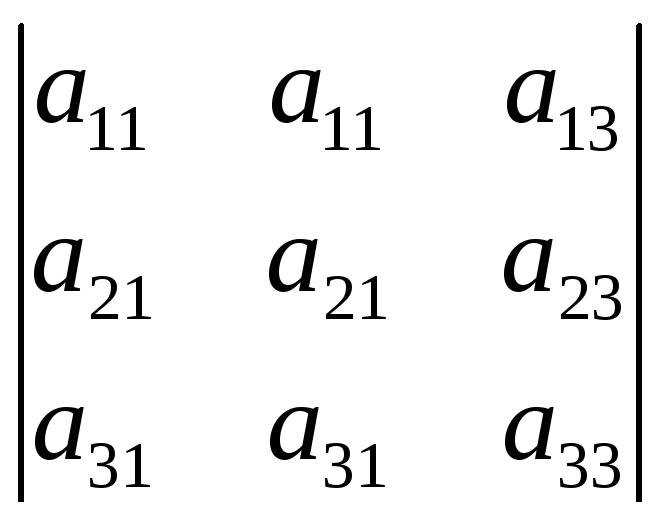 ,
т.е. ∆=–∆, 2∆=0, ∆=0.
,
т.е. ∆=–∆, 2∆=0, ∆=0.
4. Если все элементы какого-либо столбца определителя умножить на некоторое число k, то определитель умножится на это число. (Общий множитель какого-либо столбца можно вынести за знак определителя).
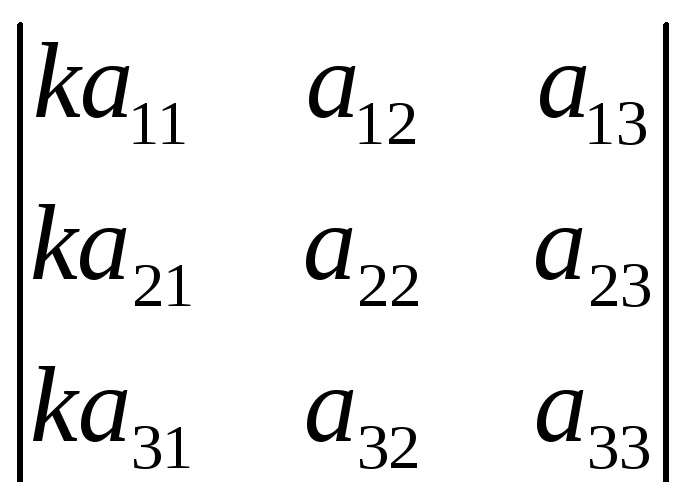 =k
=k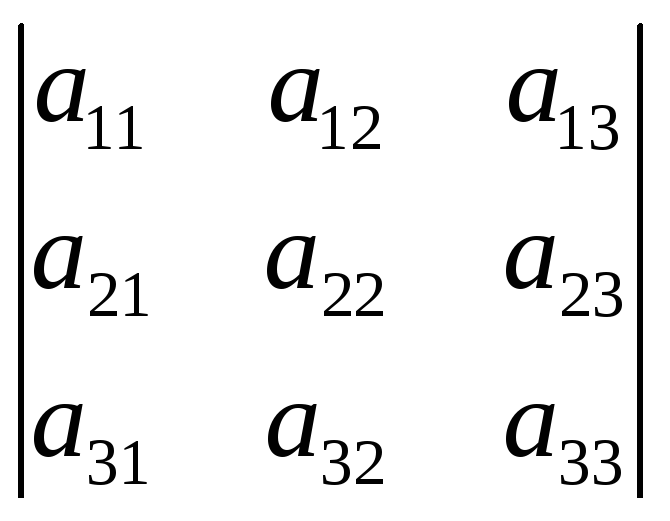 (посчитать
левый и правый и сравнить)
(посчитать
левый и правый и сравнить)
5. Если элементы двух столбцов пропорциональны, то такой определитель равен нулю.
 =4)k
=4)k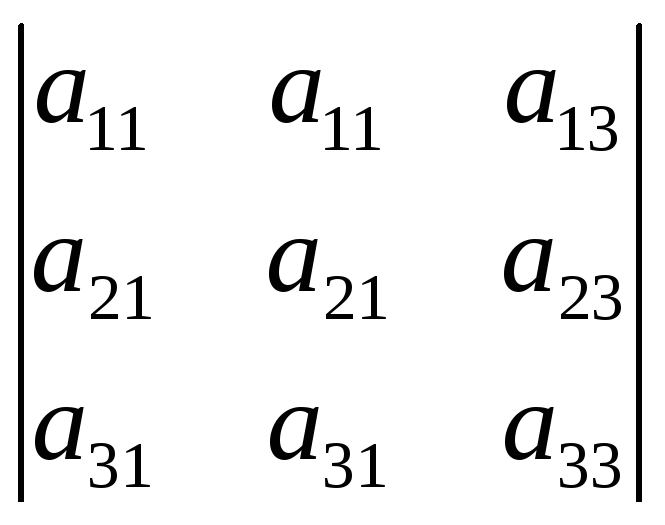 =3)0
=3)0
6. Если элементы какого-либо столбца определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
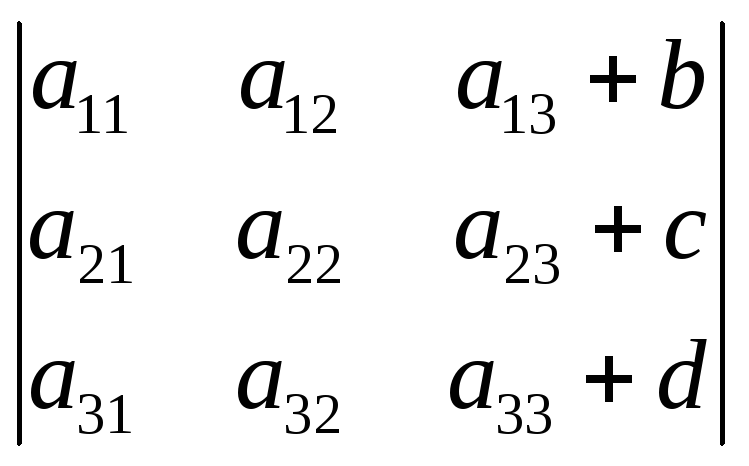 =
=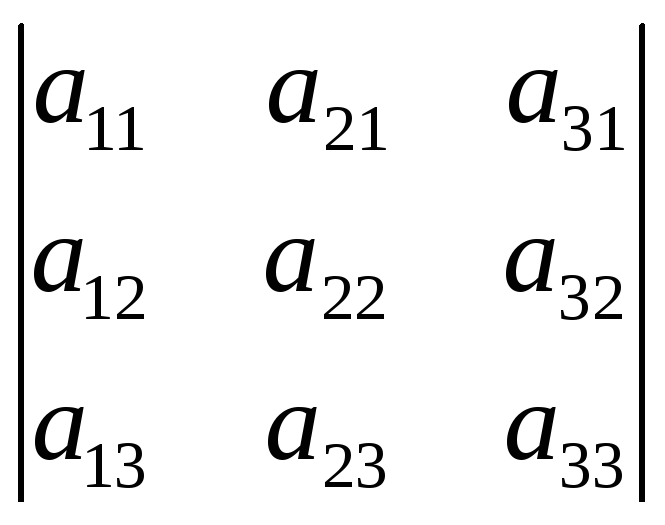 +
+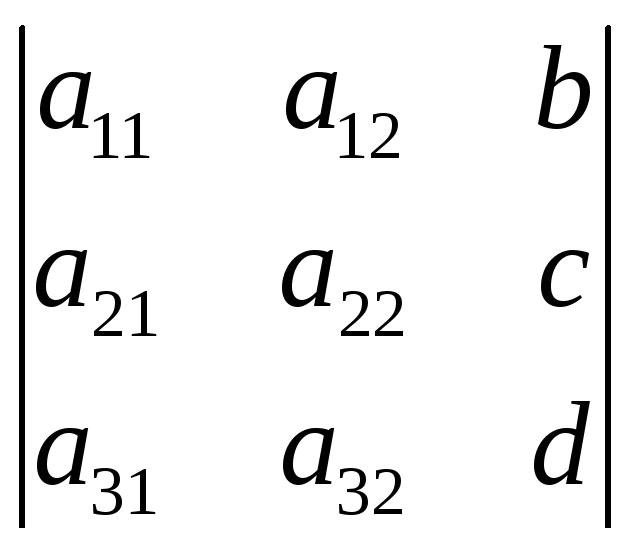 (посчитать
левый и правый и сравнить)
(посчитать
левый и правый и сравнить)
7. Определитель не изменится, если к элементам одного столбца прибавить соответствующие элементы другого столбца, умноженные на любое число.
∆ =
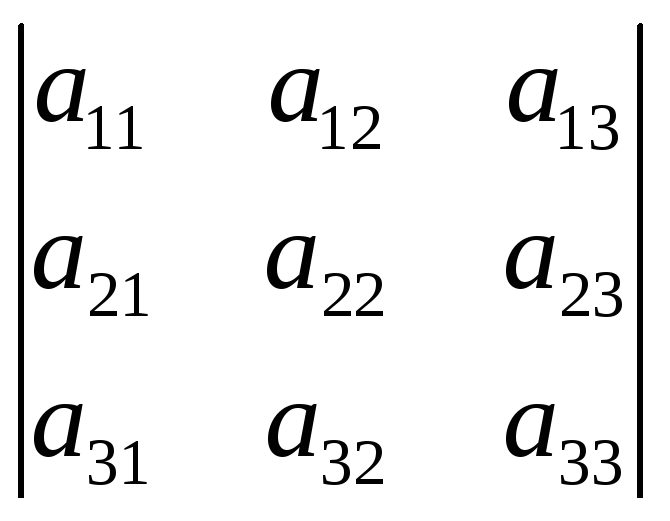 =
=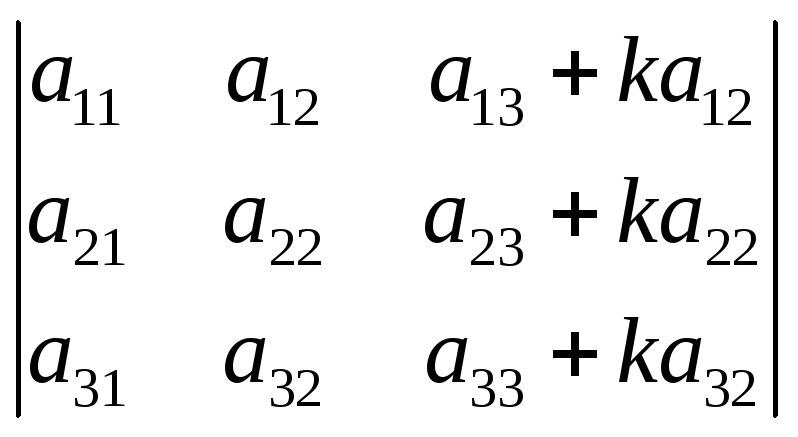
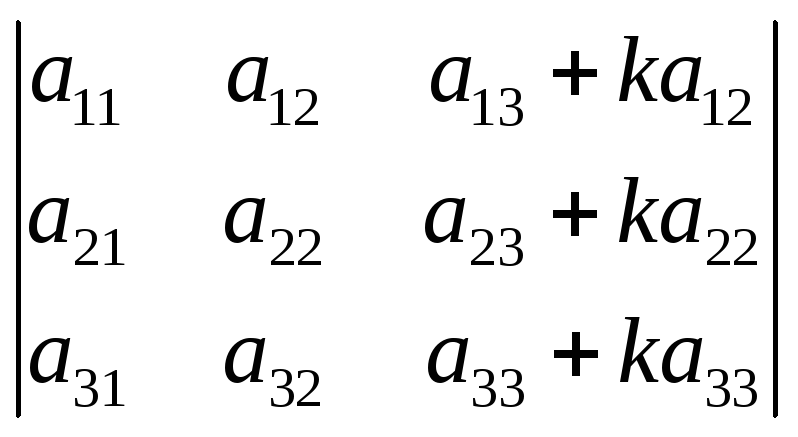 =6)4)
=6)4)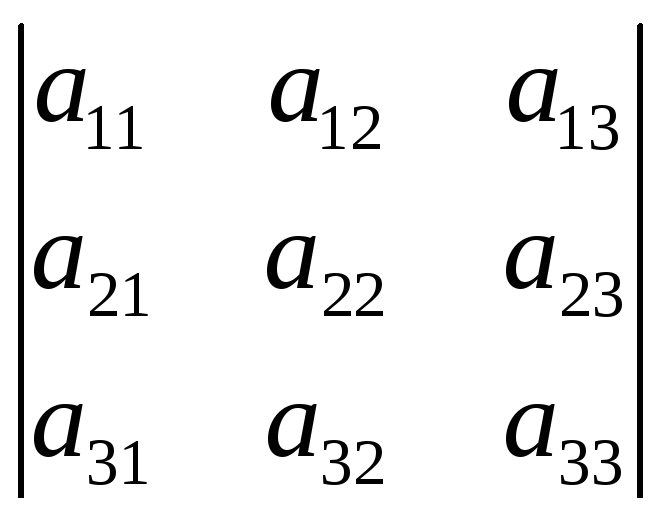 +k
+k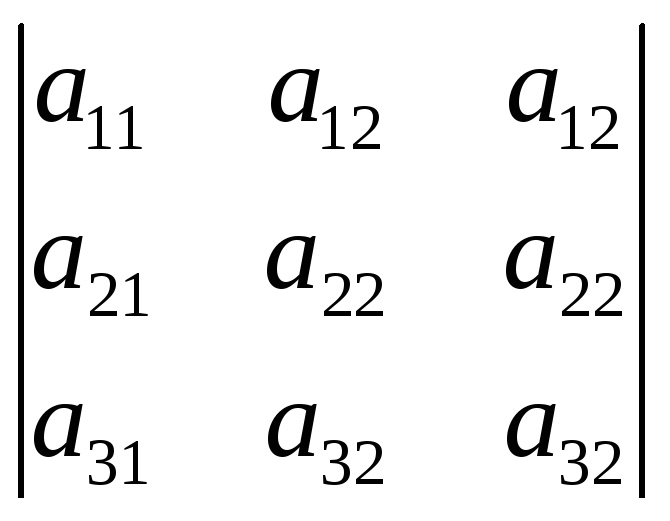 =
=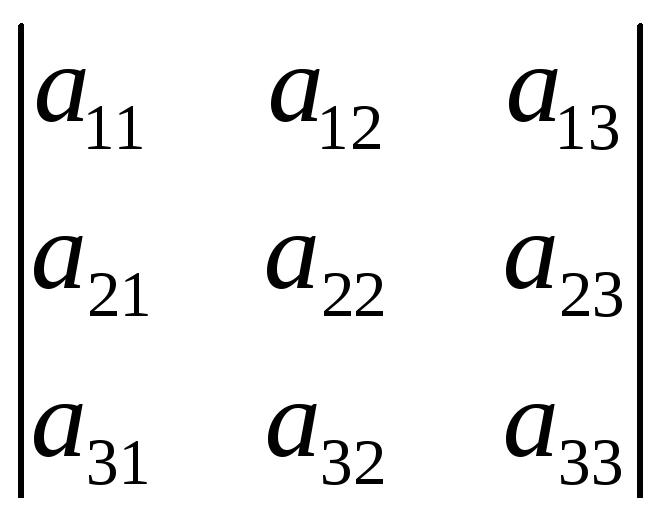 +k0 = ∆
+k0 = ∆
8. Определитель, содержащий столбец нулевых элементов равен нулю. Это св-во вытекает из 4 при k=0.
9. Определитель произведения квадратных матриц равен произведению определителей этих матриц: |А·В|=|А|·|В|.
10. Сумма произведений элементов столбца определителя на соответствующие алгебраические дополнения другого столбца равны нулю, т.е. aj1Ai1+aj2Ai2+aj3Ai3=0 (i=1,3;j=1,3;i≠j)
По определению ∆= аi1Аi1+аi2Аi2+аi3Аi3. НоAi1, Ai2, Ai3не зависят отai1. ai2, ai3 (элементовi-й строки) и если вi-й строке записать элемент другой строки, например,j-й, то получим определитель с двумя равными строками, который равен 0 по свойству 3.
Лекция 3
