- •Глава 1. Линейная алгебра.
- •§1. Матрицы и действия над ними.
- •1.1. Понятие матрицы
- •1.2. Основные операции над матрицами и их свойства.
- •§2. Определители.
- •2.1. Понятие определителя.
- •2.2. Свойства определителей.
- •§3. Обратная матрица.
- •3.1. Понятие обратной матрицы. Теорема об обратной матрице.
- •3.2. Метод элементарных преобразований.
- •§4. Системы линейных уравнений. Методы решения.
- •4.1. Понятие системы линейных уравнений.
- •4.2. Матричный способ решения слу.
- •4.3. Формулы Крамера.
- •§5. Ранг матрицы. Теорема кронекера-капелли. Решение произвольных методов гаусса. Однородные системы.
- •5.1.Ранг матрицы.
- •5.2. Методы нахождения ранга матрицы.
- •5.3. Теорема Кронекера-Капелли.
- •5.4.Решение произвольных систем методом Гаусса.
- •5.5. Однородные системы.
- •§6. Линейные и евклидовы пространства.
- •6.1. Понятия вектора, линейного пространства.
- •6.2. Линейная зависимость векторов. Базис.
- •6.3. Евклидовы пространства. Неравенство Коши-Буняковского.
5.2. Методы нахождения ранга матрицы.
1) Метод окаймляющих миноров.
При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k-го порядкаMkотличный от нуля, то требуется вычислить лишь миноры (k+1)-го порядка, окаймляющие минорMk. Если все они равны нулю, то ранг матрицы равенk. Если хотя бы один минор (k+1)-го порядка не равен нулю, то процедура повторяется.
Пример: A=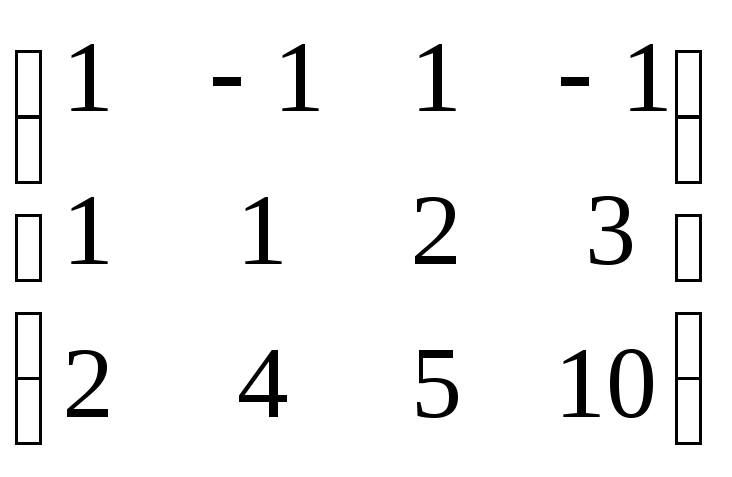
![]()
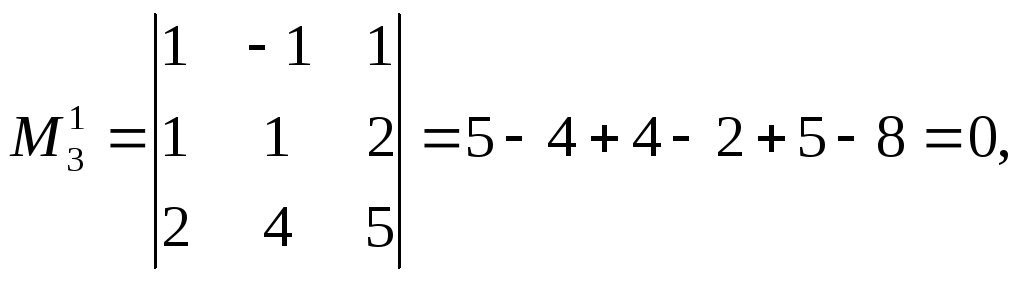
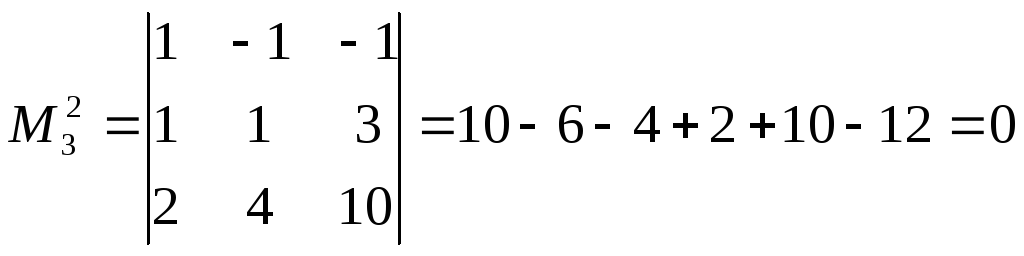 r(A)=2.
r(A)=2.
2) Метод элементарных преобразований.
С помощью элементарных преобразований приводим матрицу к трапециевидной форме, если матрица квадратная, то к треугольной. Ранг матрицы будет равен числу ненулевых строк матрицы. При элементарных преобразованиях получаются эквивалентные (равносильные) матрицы.
Пример: А = 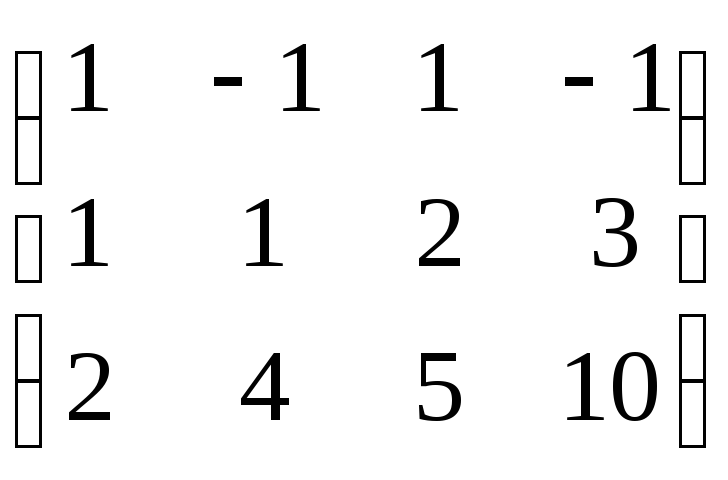


![]() r(A)=2.
r(A)=2.
5.3. Теорема Кронекера-Капелли.
Рассмотрим произвольную систему:
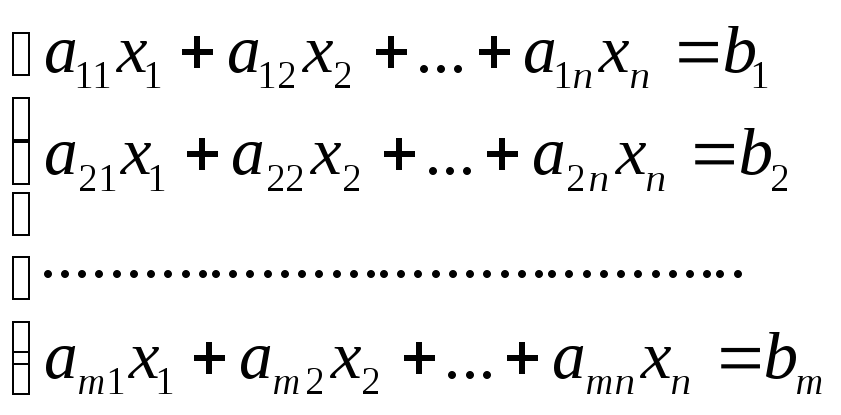 (3)
(3)
Теорема Кронекера-Капелли: Чтобы
система (3) была совместна, необходимо
и достаточно, чтобы ранг основной матрицы
системы был равен рангу расширенной
матрицы, т.е.![]() .
При этом если
.
При этом если![]() (числу неизвестных), то система
определенная. Если
(числу неизвестных), то система
определенная. Если![]() ,
то система неопределенная.
,
то система неопределенная.
5.4.Решение произвольных систем методом Гаусса.
Ранее рассматривались квадратные системы с ∆≠0. Для решения произвольных систем (3) чаще применяется метод Гаусса (метод последовательного исключения неизвестных).
При решении системы методом Гаусса выписывается расширенная матрица системы и над строками этой матрицы производят элементарные преобразования, чтобы привести матрицу к квазитреугольному виду. Находят ранги основной и расширенной матриц.
Если они неравны, то система несовместна.
Если они равны, т.е.
![]() ,
то система совместна. Если система
определенная, то из полученной матрицы
восстанавливают систему и, начиная с
последнего уравнения, находят неизвестные.
,
то система совместна. Если система
определенная, то из полученной матрицы
восстанавливают систему и, начиная с
последнего уравнения, находят неизвестные.
Если система несовместна, находят какой-либо базисный минор порядка r. Неизвестные, коэффициенты которых входят в базисный минор, называютбазисныминеизвестными (их число равно r), а остальныеn-rнеизвестных называютсвободными. По полученной матрице восстанавливают систему, базисные неизвестные оставляют в левой части уравнений, свободные неизвестные переносят в правую. Выражают базисные неизвестные через свободные. Получают общее решение системы (3).
Придавая свободным неизвестным произвольные значения, получают соответствующие значения базисных неизвестных. Таким образом, находят частные решения системы (3).
Пример: 1)
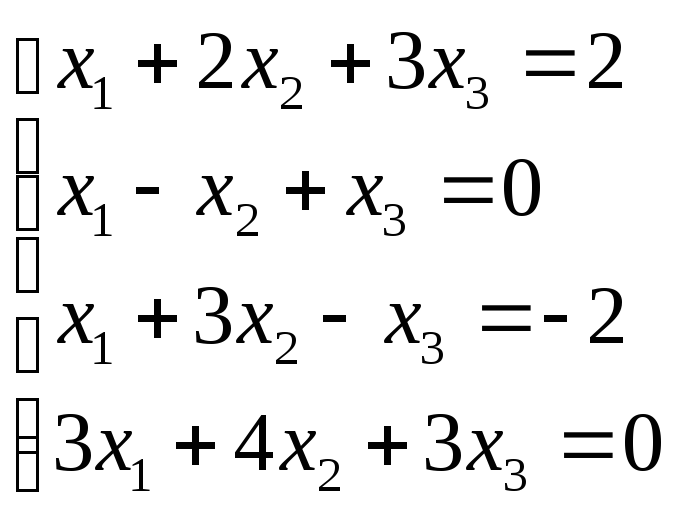
![]()
2)
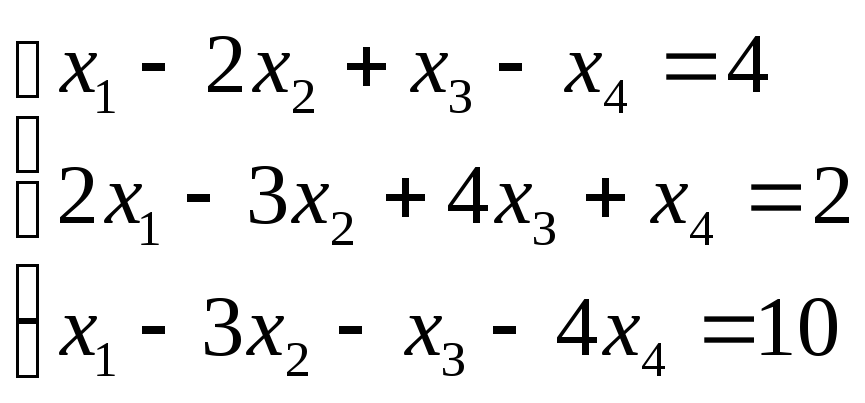
5.5. Однородные системы.
Если свободные члены в системе (3) равны нулю, то она называется однородной:
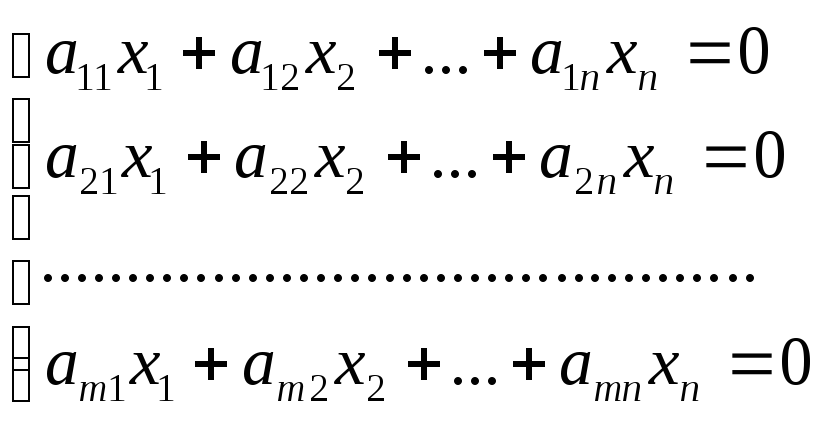 (4)
(4)
Она всегда совместна, т.к. обладает
тривиальным решением
![]() .
.
Рассмотрим условия, при которых система имеет нетривиальные решения.
Теорема 1:Для того чтобы система (4) имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е.r(A)n.
Доказательство: Еслиn=r, то из теоремы Кронекера-Капелли вытекает, что система (4) имеет единственное, а значит только тривиальное решение.
Если rn, то система (4) является неопределенной, (т.к. несовместной она быть не может) и, значит, имеет бесконечное множество ненулевых решений.
Теорема 2:Для того чтобы квадратная однородная система имела нетривиальное решение необходимо и достаточно, чтобы определитель основной матрицы системы (4) был равен нулю.
Доказательство:Если≠0, тоr(A)=n, то система имеет единственное, а значит только тривиальное решение. Это необходимое условие. Оно также является и достаточным, т.к. если=0, тоr(A)nи система имеет бесконечное множество ненулевых решений.
Для решения систем (4) удобно пользоваться
методом Гаусса. Так как r(A)n,
то система является неопределенной:
переносим свободные неизвестные (их
число равноn-r)
в правую часть уравнений. Придавая им
произвольные значения![]() ,
получимобщее решениесистемы (4):
,
получимобщее решениесистемы (4):
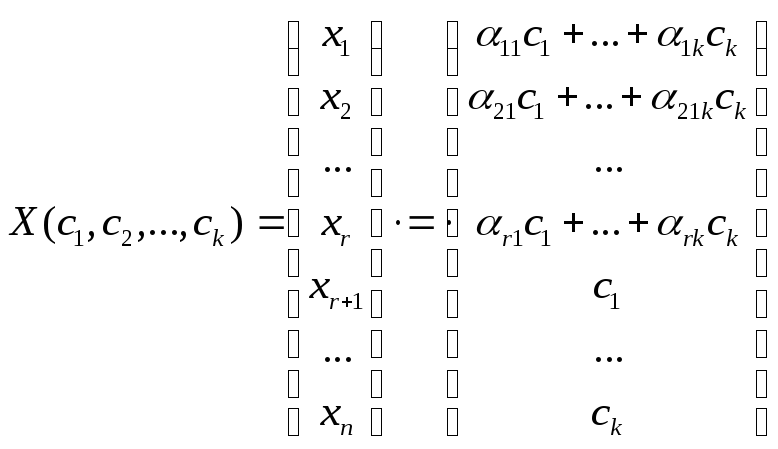
Подставляем в общее решение следующие значения переменных (свободным неизвестным придаем поочередно значение 1, полагая остальные равными 0):
![]()
![]()
………………………
![]() ,
,
получим kразличных
решений![]() Полученное множество решений называетсяфундаментальной системой решенийоднородной системы (4). С помощью
фундаментальной системыобщее решение
X системы(4) может быть записано в виде:
Полученное множество решений называетсяфундаментальной системой решенийоднородной системы (4). С помощью
фундаментальной системыобщее решение
X системы(4) может быть записано в виде:
![]()
Пример: