§3. Обратная матрица.

3.1. Понятие обратной матрицы. Теорема об обратной матрице.

Квадратная матрица называется вырожденной, если ее определитель равен нулю иневырожденной, если определитель не равен нулю.

Матрица A^-1 называется обратной матрицеA, если выполняется условие:AA^-1= A^-1A=E, гдеA^-1 ,E–матрицы того же порядка, что иA.

Матрица

A^*=, составленная из алгебраических дополнений матрицыA, причем алгебраические дополнения элементовi-й строки матрицыA расположены в i-м столбце матрицыA^*, называетсяприсоединеннойматрицей

Теорема об обратной матрице:Любая невырожденная квадратная матрица имеет единственную обратную.

Доказательство:

Докажем эту теорему на примере квадратной матрицы 3-го порядка. Найдем произведение матриц A иA^* .

A A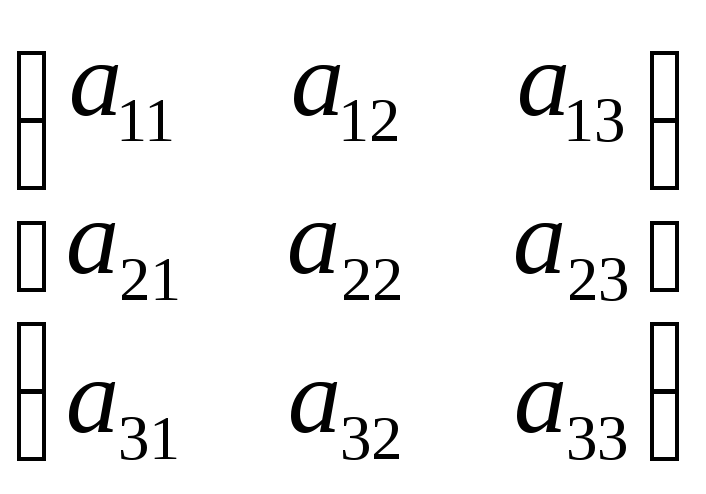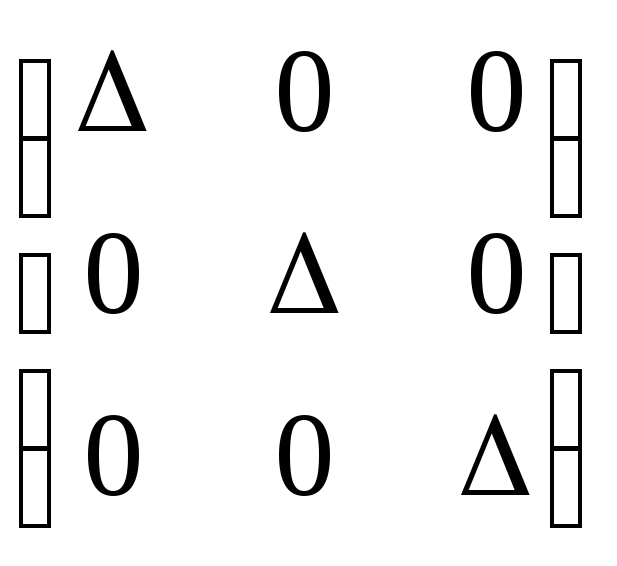^*= ·==(по определению и по св-ву 10)=∆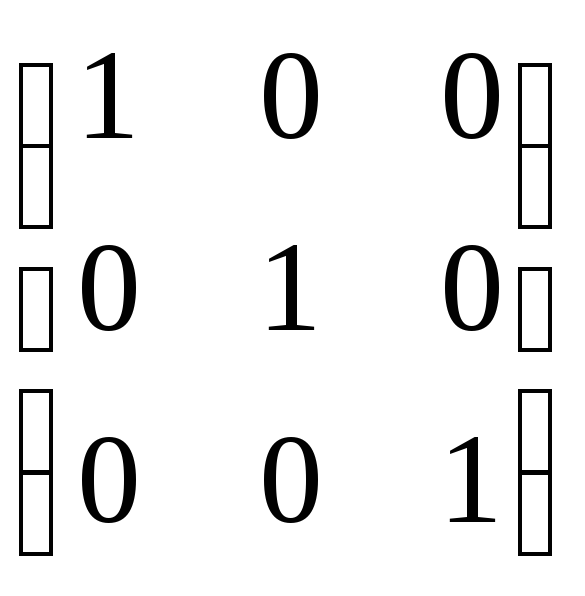= ∆·E.

Аналогично убеждаемся, что A^* A= ∆·E.

Получили A A^*=∆·EиA^* A= ∆·E. Перепишем по-другому:и(∆≠0). Сравнивая с определением обратной матрицы, получаем, т.е.

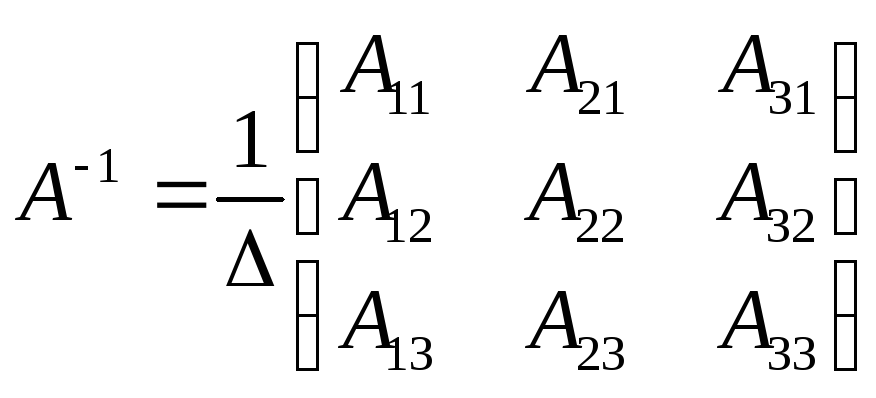(первый способ вычисления обратной матрицы)

Докажем единственность обратной матрицы:

Предположим, что для матрицы А существуют две обратныеВи С, т.е. верны равенства:АВ=ВА=ЕиАС=СА=Е. Тогда, используя 1-е свойство произведения матриц, получим:

САВ=(СА)В=ЕВ=В, САВ=С(АВ)=СЕ=С => С=В,ч.т.д.

Свойства обратной матрицы:

1. det (A^-1)=

2. (A·B)^-1=B^-1A^-1

3. (A^-1)^т=(А^т)^-1.

3.2. Метод элементарных преобразований.

Элементарными преобразованиямиматрицы называются следующие преобразования:

1) перестановка строк (столбцов),

2) умножение строки (столбца) на число, отличное от нуля,

3) прибавление к элементам строки (столбца) соответствующих элементов строки (столбца), предварительно умноженных на какое-либо число, отличное от нуля.

С помощью метода элементарных преобразований обратная матрица находится следующим образом: для матрицы А составляется прямоугольная матрицаГ_А=(А:Е) порядкаn2n. Элементарными преобразованиями приводим матрицуГ_А к виду (Е:В). ТогдаВ=А^-1.

Пример: А =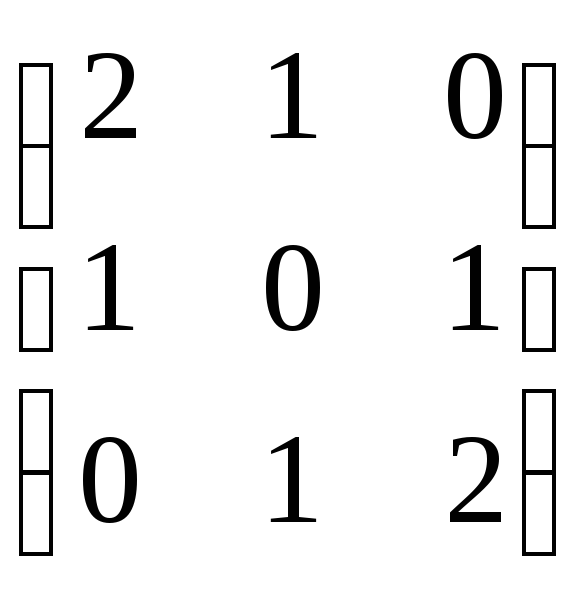1) |А| =4;А₁₁=1,А₁₂=2,А₁₃= 1,А₂₁=2,А₂₂= 4,А₂₃=2,А₃₁= 1,А₃₂=2,А₃₃=1.А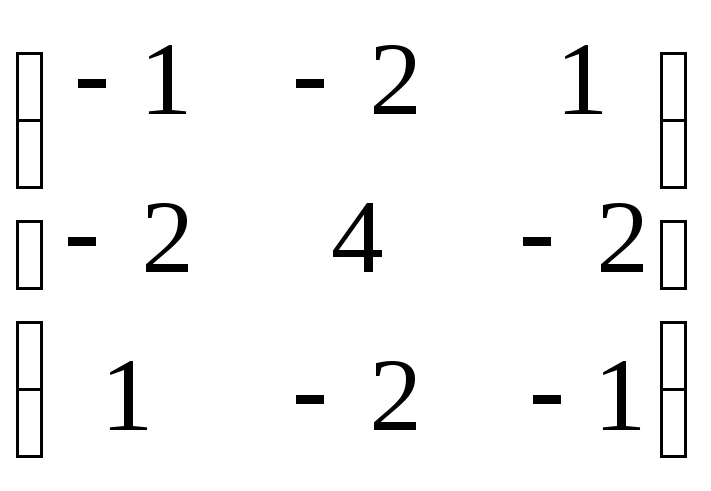^*= А^-1=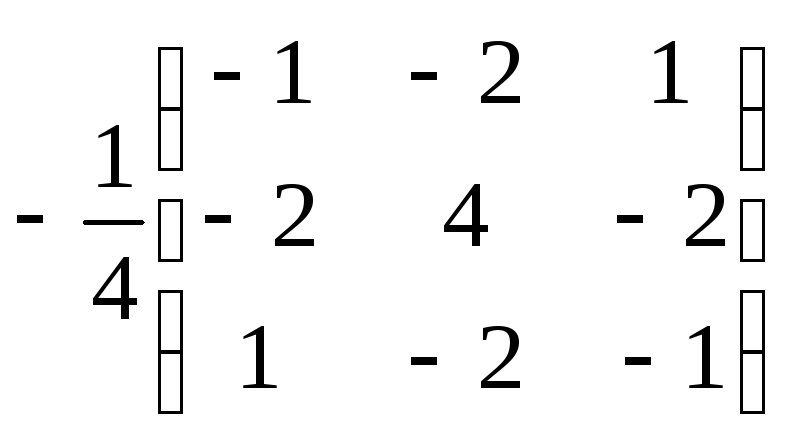

2) А =

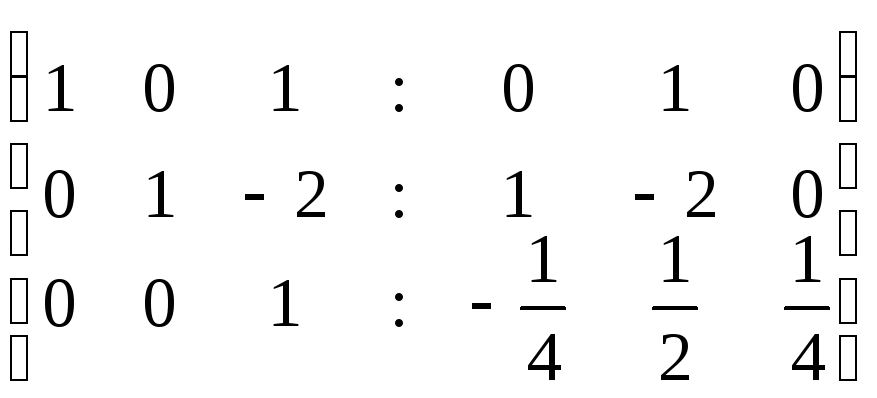
§4. Системы линейных уравнений. Методы решения.

4.1. Понятие системы линейных уравнений.

В общем случае система mлинейных уравнений сnнеизвестными имеет следующий вид:

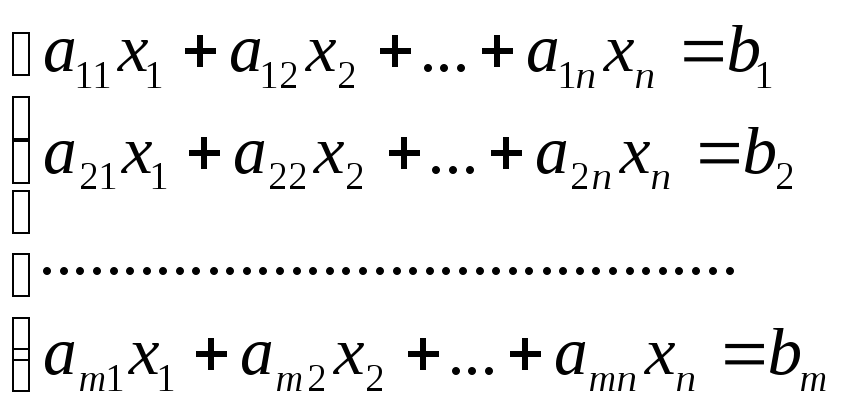(1)

При этом через x₁,x₂,…,x_nобозначенынеизвестные, подлежащие определению; величины,…,называютсякоэффициентами системы, и величины,…,, называемыесвободными членами, предполагаются известными.

Система называется однородной, если все ее свободные члены,…,равны нулю. Если хотя бы один из свободных членов,…,отличен от нуля, то система (1) называетсянеоднородной.

Система называется квадратной, если число составляющих ее уравнений равно числу неизвестных (т. е.m=n).

Решением системы(1) называется такая совокупностьnчиселс₁,…,с_n, которые при подстановке в систему (1) вместо неизвестныхx₁,x₂,…,x_n обращает каждое уравнение этой системы в тождество.Решить систему(1) – значит найти все ее решения или доказать, что их нет.

Если система имеет хотя бы одно решение, то она называется совместной, а если не имеет –несовместной. Если совместная система имеет только одно решение, то ее называютопределенной, если более одного решения – тонеопределенной.

Коэффициенты системы можно записать в виде матрицы

А=,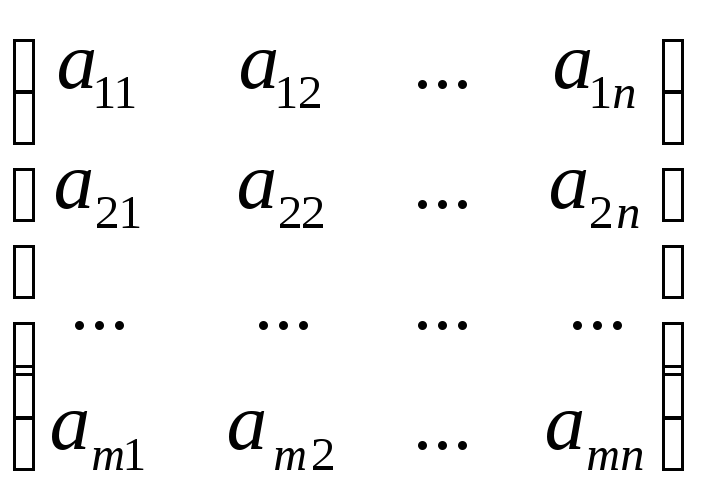

которая называется основной матрицей системы. Числа,…,образуют столбец, называемый столбцом свободных членовB=. Основная матрица системы, дополненная справа столбцом свободных членов, называетсярасширенной матрицей системыи обозначается

Ā=