5. Основные методы интегрирования

Искусство интегрирования состоит в умении отыскать такие тождественные преобразования подинтегрального выражения, которые сводили бы интеграл к табличному.

5.1 Непосредственное интегрирование

Непосредственное применение табличных интегралов с использованием основных свойств неопределённых интегралов.

Примеры:

1.

Проверка:

2.

Проверка:

3.

Проверка:

4.

Проверка:

5.2 Метод замены переменной

Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла ∫ f (x) dx в интеграл F(u)du, который легко вычисляется по какой-нибудь из основных формул интегрирования.

Для нахождения интеграла ∫ f (x) dx заменяем переменную x новой переменной u с помощью подстановки x=φ(u). Подставляя в подынтегральное выражение вместо x и dx их значения, выраженные через u и du, имеем

∫ f (x) dx=∫ f [φ(u)] φ^/ (u) du=∫ F (u) du.

После того как интеграл относительно новой переменной u будет найден, с помощью подстановки u =ψ (x) он приводится к переменной x.

Примеры: Пользуясь методом замены переменной найти интегралы:

1.

3x-1=u

3dx=du

dx=1/3du

= = =

2.

3

-3x²+1=u

-6xdx=du

xdx=-du/6

.

=

=

4.

5.

6.

7.

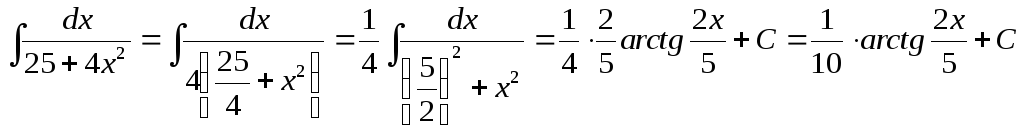
5.3 Интегрирование по частям

Пусть u=u(x) и v=v(x) – две дифференцируемые функции. Найдём дифференциал от произведения этих функций.

duv= udv + vdu

Отсюда, интегрируя, получаем

∫ duv = ∫ udv + ∫ vdu

uv = ∫ udv + ∫ vdu

Формула интегрирования по частям:

(9)

С помощью формулы интегрирования по частям вычисление интеграла ∫udv сводится к вычислению интеграла ∫vdu, если последний окажется проще исходного.

Полезно запомнить следующие типы интегралов, вычислять которые удобно интегрированием по частям:

а) ;;

u=P(x)

; ;

б) ;;

; ;

dv=P(x)dx

в) ;

u=e^x

;

Примеры:Используя формулу интегрирования по частям (9), найти интегралы:

u=lnx dv=dx

du=1/x dx v=x

=

1.

=

=

u=arcsin x dv=dx

du=1/v=x

2.

1-x²=t

-2xdx=dt

xdx=-1/2dt

=

6. Варианты для самостоятельной работы

Вариант 1 Найдите следующие интегралы

Вариант 2 Найдите следующие интегралы

Вариант 3 Найдите следующие интегралы

Вариант 4 Найдите следующие интегралы 10) 11) 12)

Вариант 5 Найдите следующие интегралы

Вариант 6 Найдите следующие интегралы

7. Образец решения варианта 1

	формула
	формула

8. Тесты

1. Неопределенный интеграл равен

А.

Б.

В.

Г.

2. Первообразная для функции

y = x³ – 2 имеет вид

А. 3x² + C

Б. 3x⁴ – 2 x + C

В. 6x⁴ - 2 + C

Г. x⁴/4 - 2x + C

3. 3 равен

А. 3 arctgx + C

Г.

В.

Г. -3 arctgx + C

4. 7^х dx равен

А. 7^xln7 + C

Б.

В. x7^x-1 + C

Г. 7^x-1 + x + C

5. Первообразная для функции y = 2x + e^x имеет вид

А. хе^x + С

Б. х²е^x-1 + С

В. x² + е^x +С

Г. 2xe^x+1 + C

6. 5sinx dx равен

А. -5сosx + C

Б. 5cosx + C

В. cos5x + C

Г. – cos5x + C

7. равен

А. ctg3x + C

Б.

В. 3ctg3x + C

Г.

8. cos 3xdx равен

А. sin 3x + C

Б. 3cos3x + C

В.

Г.

9. 2xdx равен

А. х² + С

Б. 2 + С

В. 2х +C

Г. 2

10. 7e^x dx равен

А. 7е^x-1 + С

Б. 7е^x + С

В. 7е^x+1 + С

Г. e^xln7+ C

11. равен

А. – arctgx + C

Б. arctgx + C

В. –arcsinx + C

Г. arcsinx + С

12. Первообразная для функции y = 3x² имеет вид

А. 6x² + C

Б. x³ + C

В. 8x⁴ + C

Г. 6x⁴ + C

13. равен

А.

Б.

В.

14. равен

А. 5ctgx + C

Б.

В. -5ctgx + C

Г.

15. х⁵ dx равен

А. 5x⁴ + C

Б. х⁶/6 + C

В. 5x⁶ + C

Г.

16. 8 dx равен

А. 8 + С

Б. 8х + С

В. 8х

Г. 8

17.равен

А.

Б.

В.

Г.

18. (5-x) dx равен

А. - 1

Б. 5x –х²/2 + С

В. (5-x)² + c

Г. 5- x + C

19. равен

А. 7tgx + C

Б.

В. tg⁷x + C

Г. 7tg7x + C

20. (8 / x)  dx равен

А. 8x² + C

Б. 8lnx+ C

В. 8x^-2 + C

Г. 8x^-1 + C

21. равен

А. 3tgx + C

Б. 3tg3x + C

В.

22. равен

А.

Б.

В.

Г.

23. Первообразная для функции y = 7e^x имеет вид

А. 7е^x +С

Б. 7хе^x + С

В. 7хе^x-1 + С

Г. 7xe^x+1 + C

9. Библиографический список

1. Пехлецкий И.Д. Математика: учебник / И.Д, Пехлецкий. – М.: Мастерство, 2001. – 304 с.

2. Владимирский, Б. М. Математика. Общий курс: учебник / Б. М. Владимирский, А. Б. Горстко, Я. М. Ерусалимский. - СПб.: Лань, 2006. - 958 с.

3. Балдин К.В. Математика: [учеб. пособие для вузов / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - М.: ЮНИТИ-ДАНА, 2006. - 543 с.

4. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений / Н.В. Богомолов. – М.: Высш. шк., 2002 - 495 с.

5. Филимонова Е.В. Математика: учебное пособие для средних специальных учебных заведений / Е.В. Филимонова – Ростов н/Д: Феникс, 2003. – 384.

3