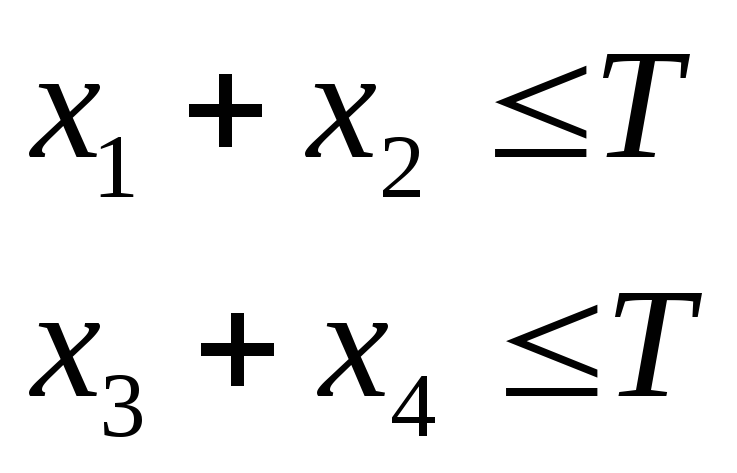Управление непрерывными статическими тп

Методы решения задач статической оптимизации

Задачи оптимизации встречаются во многих видах деятельности человека. Особое значение они имеют в технике и экономике. На теоретической базе решения оптимальных задач создаются АСУ П и ТП, локальные оптимальные и адаптивные системы управления машинами, механизмами и устройствами.

Различают задачи статической и динамической оптимизации. В задачах статической оптимизации уравнения движения модели ТП и уравнения цели являются алгебраическими, в задачах динамической оптимизации уравнения движения модели представляются системой дифференциальных уравнений, а уравнения цели (или критерий оптимальности) является интегральным функционалом.

Таким образом, методы решения задач статической оптимизации относятся к разделу поиска экстремума функций(экстремальные задачи), а методы решения задач динамической оптимизации относятся к разделу поиска экстремумафункционалов(оптимальные задачи).

Методы статической оптимизации. Решение экстремальных задач. Классификация экстремальных задач

Останавливаться на задаче поиска экстремума функции одной переменной не будем, т.к. эта задача является частным случаем задачи поиска экстремума функции многих переменных (ФМП). В общем случае можно выделить 2 задачи:

Задача 1:Найти минимум (или максимум, будем говорить о минимизации, т.к. задачу поиска максимума можно получить из задачи на поиск минимума сменой знака) ФМП на открытом множестве М.

, где

Задача 2:Найти минимум ФМП на замкнутом множестве

, где

Т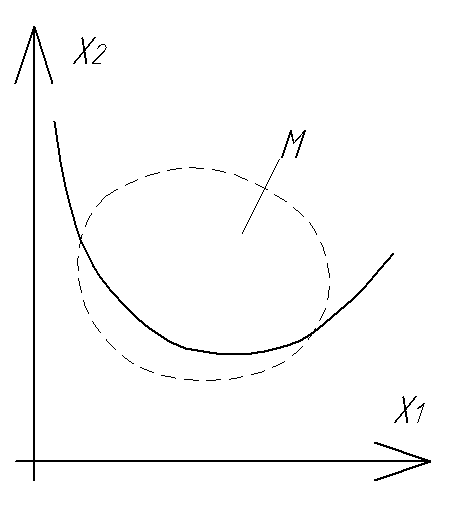.е. прии замкнутом множестве: (см. рис).

Задача 2 общая, поэтому она конкретизируется:

1. Найти минимум линейной функции (или формы) при линейных ограничениях:

при , гдеj=1–m,

или в матричной форме:

при

Примером задачи линейного программирования (ЛП) может служить задача о распределении мощности оборудования.

Пусть задано время Т. Требуется выпустить N₁продукции вида П₁иN₂продукции вида П₂с наименьшими затратами. Пусть имеются две машины А и В, которые могут выпускать как П₁так и П₂.

Машина	Производительность (продукт/ед. времени)		Время работы машины		Затраты на производство одного изделия в ед. времени
	П1	П2	П1	П2	П1	П2
А	a1	a2	x1	x2	1	2
В	b1	b2	x3	x4	1	2

Математическая постановка задачи:

Требуется минимизировать функцию, учитывающую общие затраты на производство: при выполнении ограничений:

По времени:
По выпуску:

Задача может быть поставлена и по другому, например, это может быть задача о минимизации времени, либо максимизации выпуска продукции и т.д. Однако, нельзя требовать выполнения сразу нескольких условий, т.к. такая задача будет некорректной с математической точки зрения.

2. Найти минимум ФМП при ограничениях-равенствах.

при ограничениях

Эта задача получила название классической задачи Лагранжа на условный экстремум.

3. Найти минимум ФМП при ограничениях-неравенствах.

при ограничениях

Эта задача называется неклассической задачей. Она конкретизируется следующим образом:

1. Функция 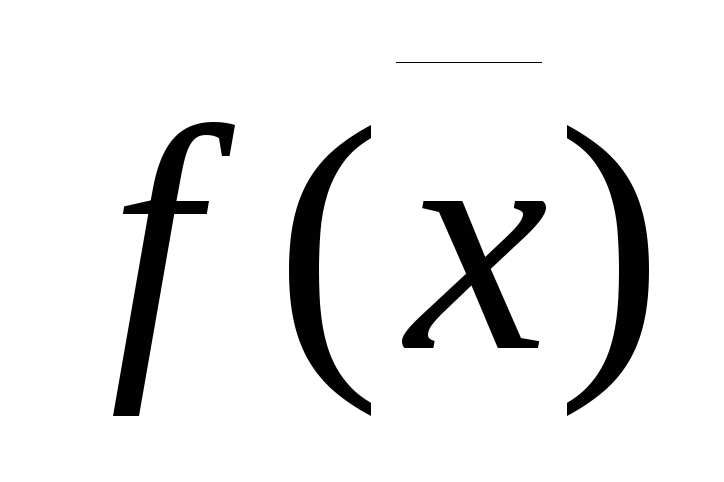– квадратичная, ограничение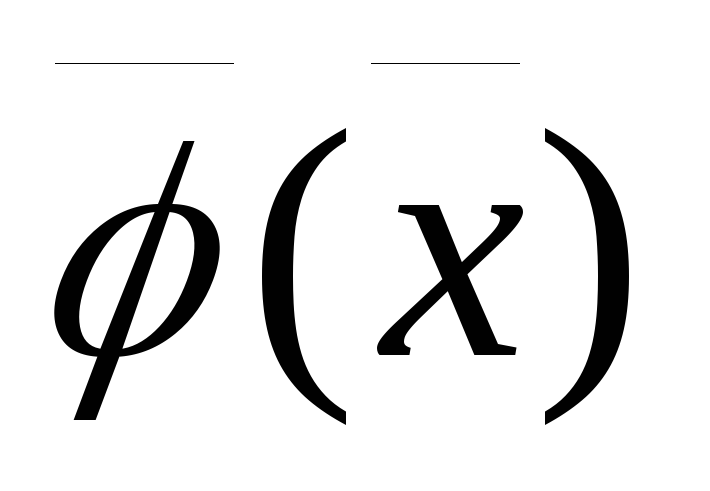– линейная или наоборот. Данная задача называется задачей квадратичного программирования.

Например, имеется два насоса для перекачки жидкости, включенных параллельно. Общий расход воды Q. Мощность, потребляемая машинами, зависит от квадрата объема перекаченной жидкости:, гдеk₁,k₂– коэффициенты, характеризующие состояние насосов.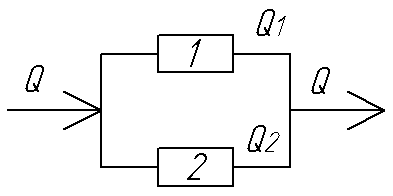Общий объем перекачанной жидкости:

Постановка задачи может быть следующей: либо найти минимум мощности при заданном Q, либо при заданномNнайти максимумQ.

2. Функция цели является выпуклой и ограничения являются выпуклым множеством. Задача решается методами выпуклого программирования.

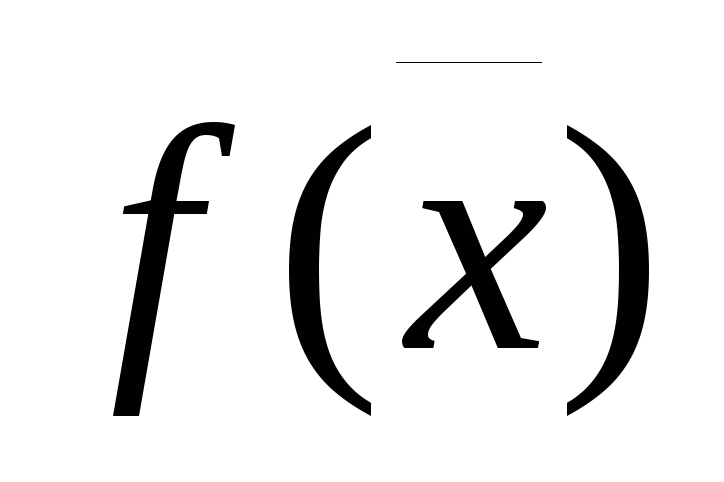3. Функция и ограничения могут быть любыми. Это задача нелинейного программирования.

Н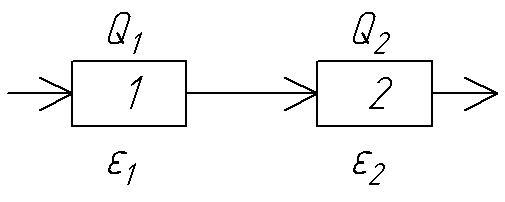апример, пусть при последовательном соединении компрессоров требуется получить максимальную степень сжатия при заданном потреблении мощности. Мощность, потребляемая каждым компрессором, прямо пропорциональная степени сжатия:, гдеk₁,k₂– коэффициенты, характеризующие состояние компрессоров. Общая степень сжатия

Все рассмотренные задачи объединяются общим термином – задачи математического программирования.