Градиентные методы.

В градиентных методах направление движения к экстремальной точке выбирается по градиенту или антиградиенту, а шаг^kвыбирается различными способами в зависимости от метода.

Метод наискорейшего спуска.

Пусть задана сепарабельная функция и начальная точка х⁰=(–0,6;–2,6), у⁰=4,68. Вычислим в точке х⁰проекции градиента:

Построим на графике линий равного уровня проекции градиента в определенном масштабе и результирующий вектор L₁, который дает направление наибольшего изменения функции в точке х⁰. Если провести черезL₁плоскость, перпендикулярную {x₁,x₂}, то эта плоскость, рассекая поверхность, выделит на ней параболу. Теперь надо найти точку экстремума полученной параболы. Для этого следует записать уравнение параболы в данной плоскости (плоскости градиента) с помощью параметра, учитывающего направление антиградиента:

Подставляя значения координат и проекций градиента, получим:

Определим параметр исходя из экстремума функции:

,

Теперь определим координаты точки х⁽¹⁾, в которой функцияпо направлениюL₁достигает экстремума.

,

,

Значение функции в этой точке: у⁽¹⁾=1,3. Полученная точка х⁽¹⁾по направлениюL₁показана на рисунке. Линия градиента касается в этой точке линии равного уровня функции у.

Продолжая вычисления, а именно: 1) определяя проекции градиента, 2) составляя уравнения параболы в плоскости градиента , 3) находя параметриз условия экстремума функции, 4) определяя координаты точки х⁽²⁾, в которой функцияпо направлению градиента достигает экстремум, получим следующие результаты:

Итерация	0	1	2	3	4	5
х	(-0,6;2,6)	(-0,08;1,82)	(0,48;2,19)	(0,65;1,94)	(0,83;2,06)	(0,89;1,98)
у	4,68	1,3	0,41	0,14	0,043	0,014

В математике доказывается, что метод наискорейшего спуска сходится. Значит, вычисления можно прервать на любом шаге, если выполнена заданная точность. Например, если задана точность по значениям функции у на смежных шагах 0,05. Тогда разность на 4 и 5 итерациях, следовательно, на пятой итерации вычисления можно закончить.

Метод наискорейшего спуска в изложенном выше пошаговом варианте достаточно универсален и применим для широкого класса функций, имеющих конечную производную в каждой точке, т.е. гладких. Но уравнение для иногда получается сложным и громоздким. Для квадратичных функций определениеможно упростить и сделать более удобным для расчетов на ЭВМ.

Пусть дано квадратичное уравнение в матричной форме:

,

которое запишем в развернутой форме через матрицу Н и С:

Запишем градиент функции у:

Возьмем теперь любое направление Sс проекциямиS₁иS₂и составим для этого направления уравнение экстремальной линии через параметрдля любой точки (х₁, х₂):

Раскрыв скобки и продифференцировав по , получим:

Отсюда определяем из условия экстремумапо:

Нетрудно заметить, что данное выражение можно переписать так:

,

что соответствует матричной записи:

Если вместо произвольного направления взять градиент, то получим:

, или:

, (6)

В общем виде, для функции многих переменных:

П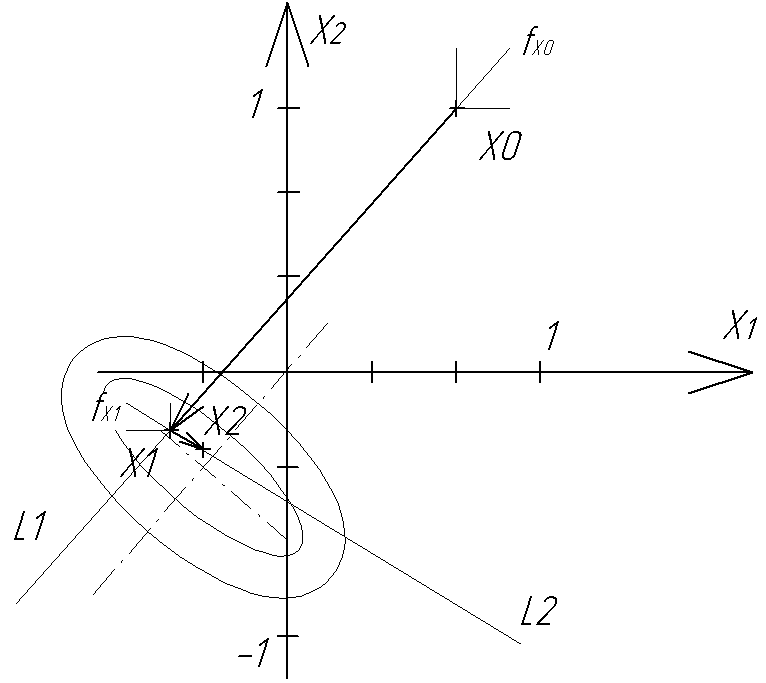окажем, насколько упростилась процедура определениядля квадратичной функции. Зададимся начальной точкой с координатами.

Определим проекции градиента в точке х⁰:

На рисунке показаны линии уровня и проекции градиента. Определяем по (6):

Координаты экстремальной точки по L₁:

;

Далее вычисляются проекции градиента во вновь найденной точке :

, и строится направлениеL₂. Затем вычисляетсядля второй итерации по (6):.

Координаты экстремальной точки по направлению L₂:

Как видно, за две итерации методом наискорейшего спуска была достигнута малая окрестность экстремума функции. В этом и состоит основное преимущество данного метода над методом Зейделя-Гаусса.