Метод сопряженных направлений

В заключение изучения приближенных методов поиска экстремума ФМП без ограничений рассмотрим метод сопряженных направлений, который завоевывает на практике все большую популярность.

Сначала дадим понятие сопряженности. Пусть имеем два направления, которые характеризуются векторами и. Направленияиназывают сопряженными по отношению к некоторой положительно определенной матрице Н, если выполняется соотношение

, (7)

С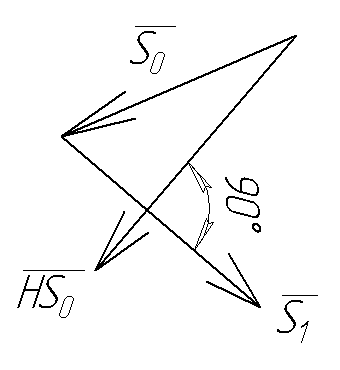опряженность связана с ортогональностью. Если Н – единичная матрица, то приимеем два взаимно перпендикулярных вектора. Соотношение (7) можно трактовать таким образом: матрица Н, примененная к вектору, изменяет его длину и поворачивает на некоторый угол так, что новый вектордолжен быть ортогонален вектору.

С помощью метода сопряженных направлений отыщем экстремум сепарабельной функции с начальной точкой.

1) Производится выбор и в этом направлении отыскивается экстремум.

Возьмем вектор с направлениямии. Векторможно выбирать произвольно, поэтому возьмем==1. Вектордает направлениеL₁.

Проведем через L₁плоскость перпендикулярную плоскости {x₁,x₂}. Плоскость пересечет экстремальную поверхность у(х₁, х₂) и выделит на ней экстремальную линию. Определим координаты минимума на этой линии (параболе), для чего вычислим проекции градиента в точке х⁰:

,

и по формуле (6) найдем :

Тогда:

Естественно, линия L₁касается в точке х⁽¹⁾линии равного уровня функции у.

2) Отыскивается из условия сопряженности .

Получим сопряженный вектор с проекциямии, воспользовавшись формулой (7):

Получили одно уравнение с двумя неизвестными. Т.к. нам требуется только направление вектора, а не его длина, то одним из неизвестных можно задаться произвольно. Пусть=1, тогда= –4.

3) Из точки х⁽¹⁾ в направлении ищется экстремум.

Сопряженный вектор должен проходить через х⁽¹⁾. Сделаем шаг в сопряженном направлении:

Величина шага ⁽¹⁾в х⁽¹⁾:

,

тогда

Итак, за две итерации было найдено точное значение экстремума функции у. В качестве первого вектора можно было выбрать градиент в исходной точке, процедура поиска остается при этом прежней.

В математике доказывается, что метод сопряженных направлений сходится для квадратичных функций не более чем за n итераций, где n – число переменных. Данное обстоятельство особенно ценно для практики, поэтому данный метод находит все большее применение.

Для функций более общего вида метод сопряженных направлений пока еще только разрабатывается. Основное затруднение тут состоит в том, что матрица Гессе получается функциональной, т.е. содержит переменную.

Классическая задача Лагранжа на условный экстремум (ограничения-равенства).

Пусть задана целевая функцияи ограничение-равенство (уравнение связи). Требуется найти минимумна множестве. Считаем, что функциииимеют непрерывные первые производные и являются выпуклыми или вогнутыми.

Рассмотрим геометрическую интерпретацию классической задачи. На плоскости {x₁,x₂} построим функцию, а также линии равного уровня функциисо значениямиN₁<N₂<…N_n. ЛинияN₁не имеет общих точек с, линияN₃имеет 2 общих точки си они не могут быть решением задачи, т.к.N₃>N₂. Остается линия уровняN₂, которая имеет единственную точку касания с. Абсолютный минимумN₀может не принадлежать ограничениюи поэтому не может быть решением задачи. Отсюда ясно и название «условный экстремум», т.е. такой экстремум, который достигается только на заданных ограничениях.

В точке касания с функциейпроведем касательную линиюL. Поострим градиенты функцийив точке касания, они будут лежать на одной линии, т.к. оба перпендикулярныLи направлены в разные стороны. Определим проекции градиентов на оси х₁и х₂в точке касания:

Из подобия треугольников можно записать:

–множитель Лагранжа.

или

Составим теперь функцию следующим образом:

–функция Лагранжа.

Запишем соотношения для нахождения экстремума функции F.

Как видно, получили те же соотношения, что были получены исходя из геометрической интерпретации задачи. Постоянная называется множителем Лагранжа. С помощью этого множителя задача на условный экстремум сводится к задаче на безусловный экстремум.

В общем случае, число переменных примем за n, а число ограничений заm. Тогда функция Лагранжа запишется в виде:

или в векторной форме

Для решения задачи записывается система уравнений:

, (8)

т.е. для n+mпеременных будем иметьn+mуравнений. Если система совместна, то задача Лагранжа имеет единственное решение.

Т.к. для определения экстремума использовались только первые производные, то полученные условия будут являться только необходимыми. Если функции ивыпуклые или вогнутые, то условный экстремум единственный. Если одна из функций невыпуклая, то экстремум может быть и не единственным. Кроме того, открыт вопрос о том, что найдено – минимум или максимум, хотя в инженерной практике обычно из физических соображений это бывает ясно.

Пример:Покажем технику решения задачи методом Лагранжа.

Для рассмотренного выше примера с двумя насосами, задан объем перекачиваемой жидкости:

При этом ограничении требуется найти потребляемую мощность насосов . Пусть коэффициенты равны₁=₂=1, К₁=1, К₂=1,5. Тогда целевая функция, найти минимум при ограничении:.

Процедура решения:

1. Составляем функцию Лагранжа

2. Составляется система уравнений (8):

3. Записываются Q_iчерези подставляются в третье выражение:

, ,,

Тогда координаты экстремума:

,

Пример 2:

Пусть дано последовательное соединение компрессоров. Задана требуемая степень сжатия:, которую требуется обеспечить при минимуме расхода мощности:

Решение:

1.

2.

3. ,, подставляем в выражение для:

, ,. Из физических соображений положительный корень отбрасываем, поэтому= –0,98.

Тогда координаты экстремума:

,

Как видно из приведенных примеров при решении задачи Лагранжа получаем в общем случае систему нелинейных уравнений, которую подчас трудно решить аналитически. Поэтому целесообразно применять приближенные методы решения задачи Лагранжа.