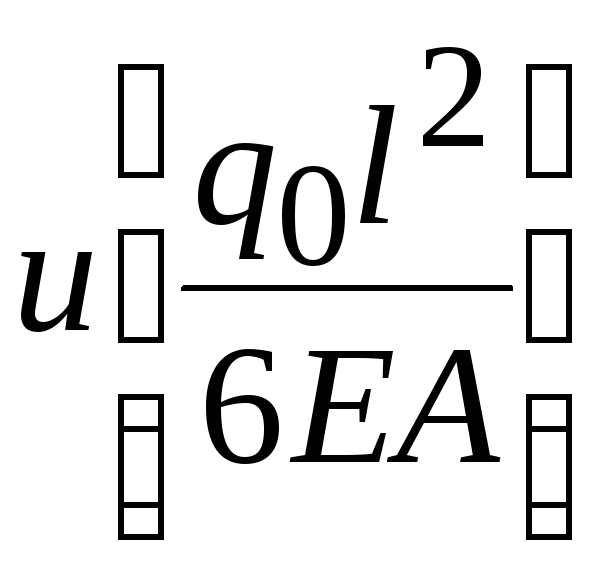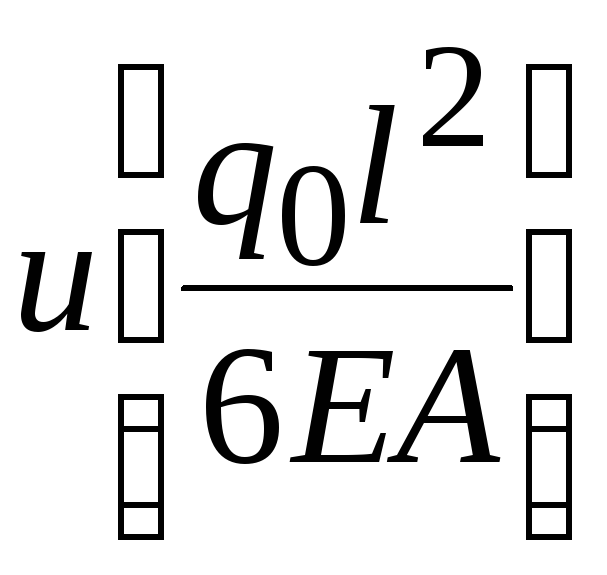Лекция 8
Рассмотрим смешанные граничные условия (вариант С).
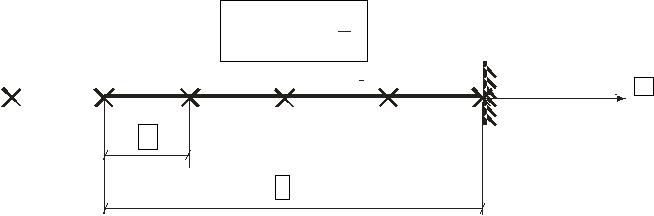
Рис. 23. Узловые точки для варианта граничных условий С
При x=0 (точка 1) статическое граничное условие N(0)=0, а значит
,
в конечно-разностной форме это выражение
имеет вид:
(2.1.29)
Такая запись накладывает дополнительные условия на область решения. Вводим «законтурную» точку (точка 0) и статическое граничное условие определяется в этом случае соотношением:
(2.1.30)
Теперь никаких дополнительных условий не накладывается. Точка 1 становится внутренней и система конечноразностных уравнений запишется так (из правого геометрического граничного условия следует, что u5=0):
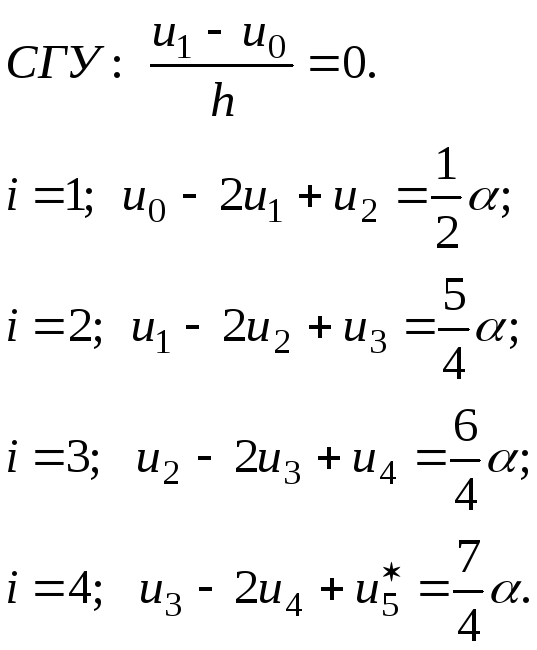(2.1.31)
Следует обратить внимание на то, что для левой крайней точки берется половина значения функции нагрузки, т. к. слева от нее стержень не существует.
Производим прямой ход исключения неизвестных верху:
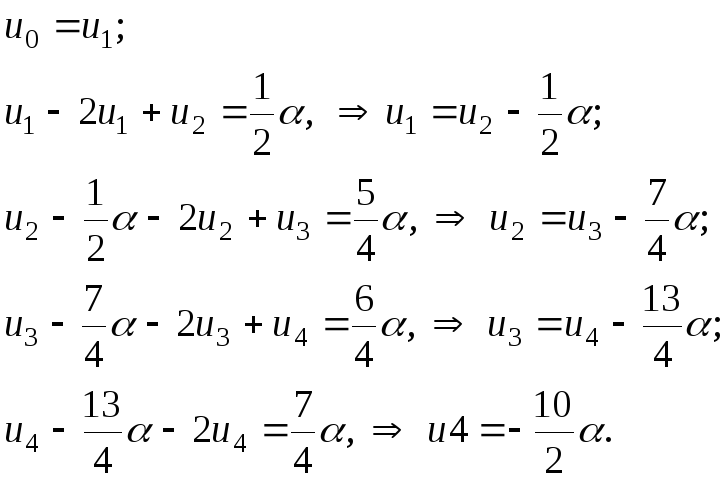(2.1.32)
Выполняем обратный ход, раскрывая и приводя полученные значения к размерности точного решения:
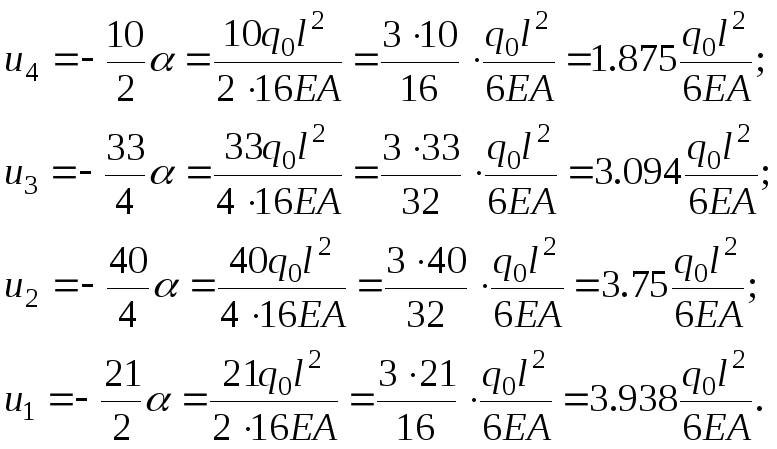(2.1.33)
Осуществим переход к усилиям в рамках МКР
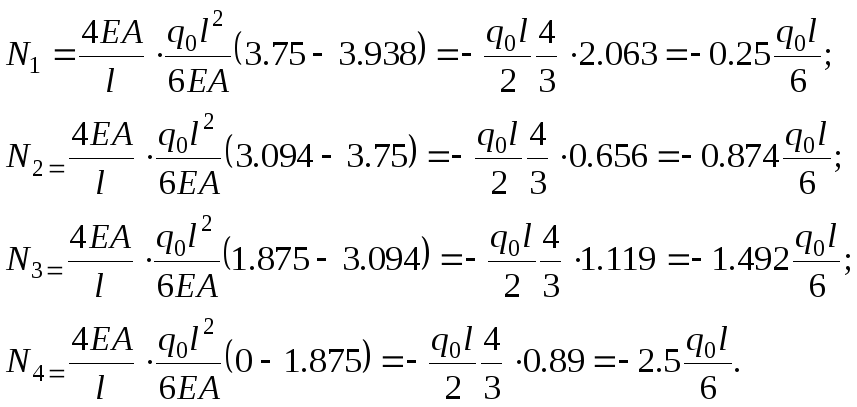(2.1.34)
Воспользуемся дифференцирующей матрицей
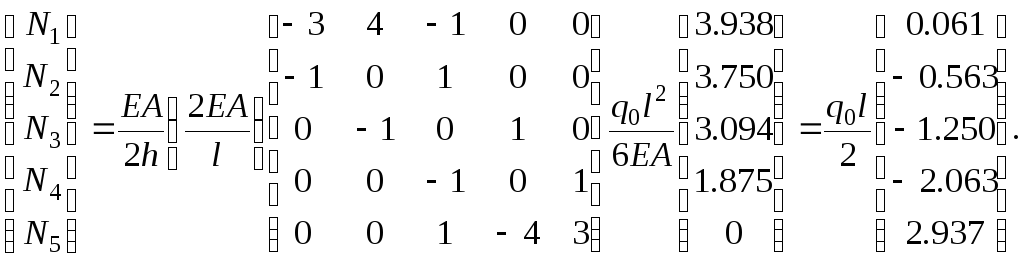(2.1.35)
Результаты расчета приведены в таблице 7 и на графике (рис. 24, 25). Звездочкой отмечены усилия, полученные в рамках МКР, двумя звездочками – усилия, полученные с помощью дифференцирующей матрицы.
Таблица 7
|
|
0 |
0.25 |
0.5 |
0.75 |
1.0 |
|
|
3.938 (4) |
3.750 (3.797) |
3.094 (3.125) |
1.875 (1.891) |
0 (0) |
|
|
-0.250 0.061 (0) |
-0.874 -0.563 (-0.563) |
-1.492 -1.250 (-1.25) |
-2.500 -2.063 (-2.063) |
- -2.937 (-3) |
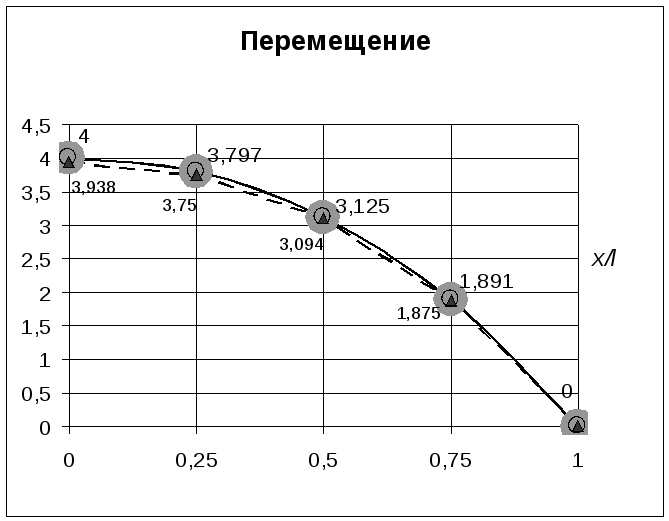
Рис 24. Изменение продольного перемещения по длине стержня (метод конечных разностей - вариант C)
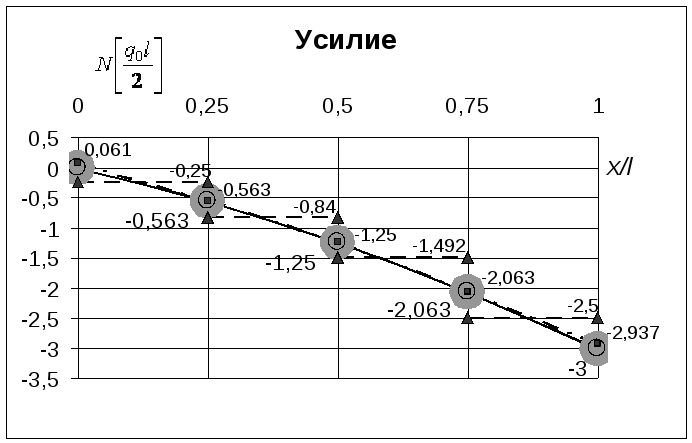
Рис. 25. Изменение продольного усилия по длине стержня (метод конечных разностей - вариант C)
Лекция 9
2.2. Метод Бубнова-Галеркина
В отличие от метода конечных разностей, где использовалась линейная аппроксимация для участков разбиения, в методе Бубнова - Галеркина аппроксимирующая функция записывается для всей области
(2.2.1)
где
- неизвестные параметры, подлежащие
определению;
- координатная функция, выбираемая таким
образом, чтобы она удовлетворяла
граничным условиям.
При внесении аппроксимирующей функции в дифференциальное уравнение
(2.2.2)
появляется
функция невязки
,
которая по физической сущности
представляет собой неуравновешенную
нагрузку.
Умножая
почленно уравнение (24) на возможное
перемещение
и интегрируя по области, приходим к
соотношению:
(2.2.3)
Первое слагаемое представляет собой работу внутренних сил на возможных перемещениях, второе – работу внешних сил, правая часть – работу невязки. Принцип возможных перемещений гласит, что сумма работ внешних и внутренних сил на возможных перемещениях равна нулю. Следовательно, неизвестные параметры находятся из условия равенства нулю работы невязки на возможных перемещениях, то есть
(2.2.4)
Определенные из (2.2.3) с учетом (2.2.4) после взятия интегралов параметры ui вносятся в выражение для аппроксимирующей функции (2.2.1). Соотношение для продольной силы получается на основании равенства (4).
Покажем ход решения методом Бубнова-Галеркина варианта А. В этом случае при геометрических граничных условиях аппроксимирующую функцию можно записать так:
(2.2.5)
Она действительно удовлетворяет граничным условиям, так как
.
Внесем соотношение (2.2.5) в уравнение упругого равновесия (5):
(2.2.6)
Умножим
почленно на
и проинтегрируем от 0 доl:
(2.2.7)
Здесь мы положили, что
Первый интеграл, входящий в (2.2.7) в силу ортогональности:
(2.2.8)
Второй интеграл возьмем по частям с учетом, что j=i.
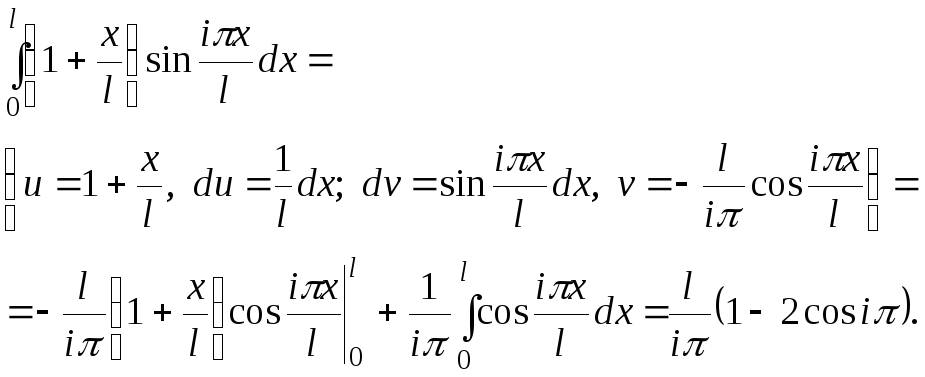(2.2.9)
Выражение (2.2.7) с учетом (2.2.8), (2.2.9) приобретает вид:
(2.2.10)
откуда
(2.2.11)
Внесем (2.2.11) в (2.2.5):
(2.2.12)
На основании равенства (4)
(2.2.13)
Найдем значения перемещения в середине пролета и усилия в начале координат, удерживая один член рядов (2.2.12) и (2.2.13) и приводя результаты к размерности точного решения.
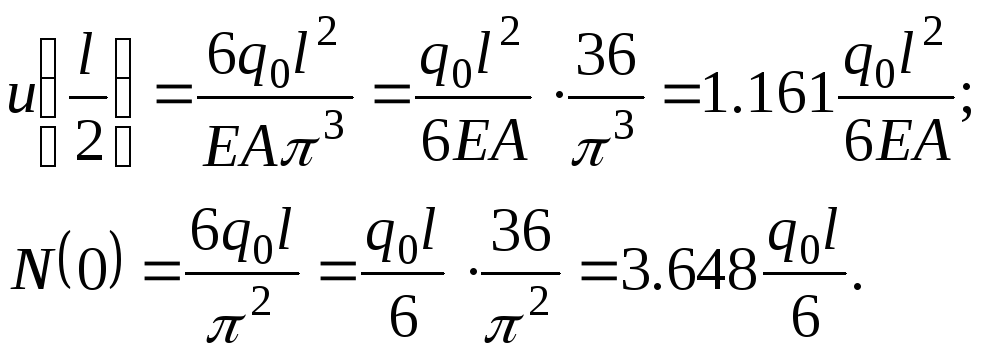
При одном члене ряда погрешность по перемещению составляет 3.2%, а по усилию – 8.8%.
Запишем программу для численной реализации зависимостей (2.2.12), (2.2.13).
Program BHА;
uses crt;
const
q=1.0;l=1.0;EA=1.0;m=4;mn=50;
var
i,j,k: integer;
dx,x,nn,uu,un,px,p:real;
u,N:array[1..m+1] of real;
BEGIN
clrscr;
dx:=l/m;
nn:=q*l*12/sqr(pi);
uu:=nn*l/(EA*pi);
Writeln;
Writeln(' Результаты расчета методом Бубнова-Галеркина ');
Writeln;
Writeln(' Координата Перемещение Усилие ');
for k:=1 to m+1 do begin
x:=dx*(k-1)/l;
u[k]:=0;
N[k]:=0;
for j:=1 to mn do begin
i:=j;
p:=i*pi;
px:=p*x;
un:=(1-2*cos(i*pi))/sqr(i);
N[k]:=N[k]+un*cos(px);
u[k]:=u[k]+un*sin(px)/i;
end;
Writeln;
Writeln (' x=',x:5:2,' u=',u[k]*uu:6:3,
' N=',N[k]*NN:6:3);
end;
readln;
END.
Результаты машинного счета представлены в таблице 8, из которой видно, что сходимость рядов по перемещениям выше, чем по усилиям. Это объясняется тем, что усилие определяется через первую производную от перемещения, а значит степень номера члена ряда, стоящего в знаменателе, на единицу меньше.
Таблица 8
|
|
|
0 |
0.25 |
0.5 |
0.75 |
1.0 |
|
|
Точн. реш. |
0 |
0.797 |
1.125 |
0.891 |
0 |
|
n=5 |
0 |
0.796 |
1.127 |
0.893 |
0 | |
|
n=10 |
0 |
0.797 |
1.126 |
0.891 |
0 | |
|
|
Точн. реш. |
4 |
2.313 |
0.25 |
-2.188 |
-5 |
|
n=5 |
3.819 |
2.265 |
0.228 |
-2.113 |
-4.579 | |
|
n=10 |
3.873 |
2.331 |
0.255 |
-2.217 |
-4.763 | |
|
n=50 |
3.975 |
2.313 |
0.25 |
-2.189 |
-4.952 |
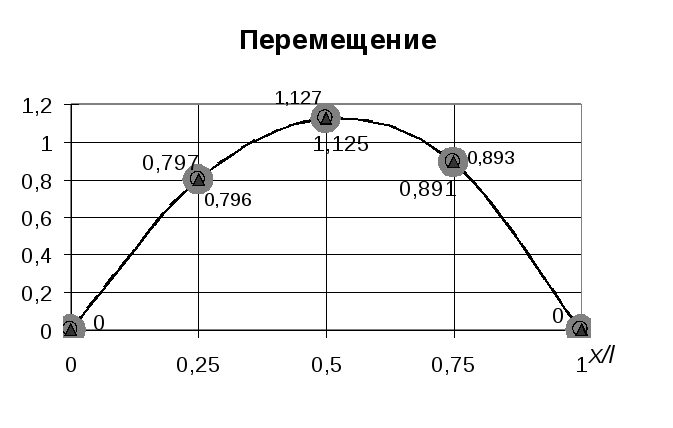
Рис 26. Изменение продольного перемещения по длине стержня (метод Бубнова-Галеркина - вариант А, число удерживаемых членов ряда - 5)
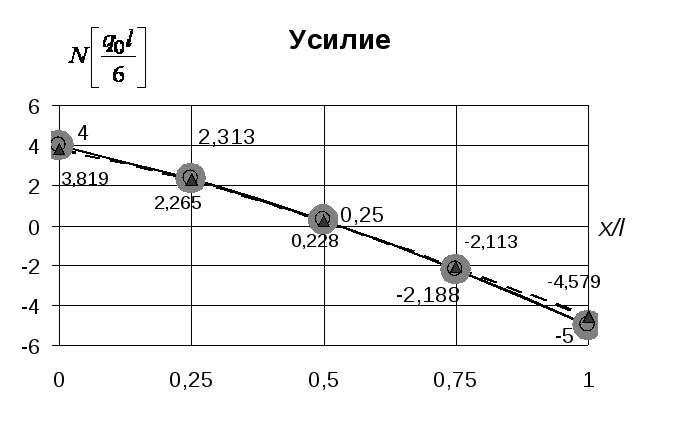
Рис 27. Изменение продольного усилия по длине стержня (метод Бубнова-Галеркина - вариант А, число удерживаемых членов ряда - 5)
Иногда решение методом Галеркина называют точным, поскольку принципиальных ограничений на число удерживаемых членов рядов нет.