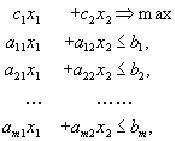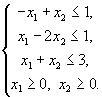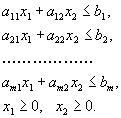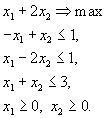Лекции 18-06-2013_16-38-06 / лекция 4

Методы математического программирования (оптимизация, линейное программирование)

1. Общая задача линейного программирования.

Исследования различных процессов, в том числе и экономических, начинаются с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения и неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих соотношениях выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.п.) Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или «математические методы исследования операций».

Математическое программирование - это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные. Оно включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Методами математического программирования решаются задачи распределения ресурсов, планирования выпуска продукции, ценообразования, транспортные задачи и т.п.

Математическое программирование возникло в 30е годы ХХ века. Венгерский математик Б.Эгервари в 1931 году решил задачу, называемую проблемой выбора. Американский ученый Г.У. Кун обобщил этот метод, после чего он стал называться «венгерским методом». В 1939 году российский ученый Л.В. Канторович разработал метод разрешающих множителей решения задач линейного программирования. Большой вклад в развитие математического программирования внесли американские ученые. В 1947 году американский ученый Дж.Данцит описал один из основных методов решения задач линейного программирования, получивший названия «симплексный».

Метод называется симплексным, так как области допустимых решений задач, которые рассматривались на начальном этапе развития метода, имели простейший (simple) вид (n=2, n=3).

Построение математической модели экономической задачи включает следующие этапы:

1. выбор переменных задачи;

2. составление системы ограничений;

3. выбор целевой функции.

Переменными задачи называются величины х₁, х₂, ..., х_n, которые полностью характеризуют экономический процесс.

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

В общем случае задача линейного программирования может быть записана в таком виде:

Z(X)=c1x1+c2x2+...+cnxn → max (min)	(1)
xj≥0,  j=1,2,...,t,    t≤n.	(2)

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор Х=(х₁, х₂, ..., х_n), удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений задачи образует область допустимых решений.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

2. Геометрическая интерпретация задач линейного программирования

Геометрическая интерпретация задач линейного программирования представима для случаев n =2 и n =3. Наиболее наглядна эта интерпретация для случая n =2, т.е. для случая двух переменных  х₁ и х₂. Пусть нам задана задача линейного программирования в стандартной форме:

х1 ≥0,  х2 ≥0

(3)

Задача линейного программирования в стандартной форме представляет собой следующее: требуется найти экстремум целевой функции при допустимой области, которая есть система линейных равенств и неравенств, а переменные неотрицательны.

Возьмём на плоскости декартову систему координат и каждой паре чисел  (х₁ , х₂) поставим в соответствие точку на этой плоскости.

Обратим прежде всего внимание на ограничения х₁ ≥0,   и х₂ ≥0. Они из всей плоскости вырезают лишь её первую четверть (рис. 1). Рассмотрим теперь, какие области соответствуют неравенствам вида а₁ х₁+а₂ х₂≤b. Сначала рассмотрим область, соответствующую равенству а₁ х₁+а₂ х₂=b. Это прямая линия. Строить её проще всего по двум точкам.

Пусть b≠0. Если взять х₁=0 , то получится х₂=b/а₂. Если взять х₂=0 , то получится х₁=b/а₁. Таким образом, на прямой лежат две точки (0,b/а₂) и (b/а₁,0). Дальше через эти две точки можно по линейке провести прямую линию (рис. 2).

Если же b=0, то на прямой лежит точка (0,0). Чтобы найти другую точку, можно взять любое отличное от нуля значение х₁ и вычислить соответствующее ему значение х₂.

Эта построенная прямая разбивает всю плоскость на две полуплоскости. В одной её части х₁+а₂ х₂<b , а в другой наоборот  а₁ х₁+а₂ х₂>b. Узнать, в какой полуплоскости какой знак имеет место проще всего посмотрев, какому неравенству удовлетворяет какая-то точка плоскости, например, начало координат, т.е. точка (0,0).

Пример

Определить полуплоскость, определяемую неравенством 4х₁-6 х₂≤ 3.

Решение

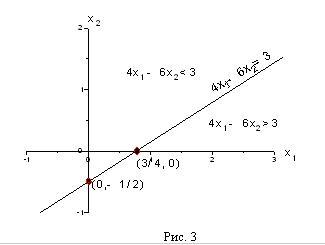
Сначала строим прямую 4х₁-6 х₂=3. Полагая  х₁=0  получим -6 х₂=3 или  х₂=-1/2. Полагая  х₂=0 получим 4х₁= 3 или х₁= 3/4. Таким образом, прямая проходит через точки (0, -1/2) и (3/4, 0) (рис. 3)

Теперь посмотрим, в какой полуплоскости лежит точка (0,0), т.е. начало координат. Имеем 4·0-6 ·0<3, т.е. начало координат принадлежит полуплоскости, где 4х₁-6 х₂≤ 3. Тем самым определилась и нужная нам полуплоскость (см. рис. 3).

Вернёмся теперь к задаче линейного программирования. Там имеют место m неравенств

(4)

Каждое из них задает на плоскости некоторую полуплоскость. Нас интересуют те точки, которые удовлетворяют всем этим m неравенствам, т.е. точки, которые принадлежат всем этим полуплоскостям одновременно. Следовательно, область, определяемая неравенствами вида (4), геометрически изображается общей частью (пересечением) всех полуплоскостей, определяемых отдельными ограничениями (к ним, естественно, надо добавить ограничения  х₁ ≥0   и х₂ ≥0 ).

Как уже говорилось выше, эта область называется допустимой областью задачи линейного программирования.

Пример

Найти допустимую область задачи линейного программирования, определяемую ограничениями

(5)

 

Решение

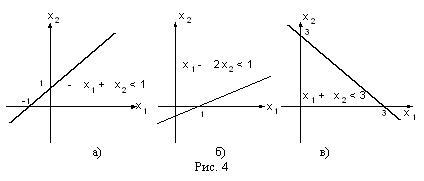
1. Рассмотрим прямую -х₁+х₂=1. При  х₁=0    х₂=1, а при  х₂=0    х₁=-1. Таким образом, эта прямая проходит через точки (0,1) и (-1,0).  Беря х₁= х₂ =0 получим, что -0+0<1 и поэтому интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4а.

2. Рассмотрим прямую х₁-2х₂=1. При х₁=0    х₂=-1/2 , а при х₂=0    х₁=1. Таким образом, эта прямая проходит через точки (0, -1/2) и (1,0). так как 0-2·0<1    (4.б).

3. Наконец, рассмотрим  прямую х₁+ х₂ =3. Она проходит через точки (0,3) и (3,0) и так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.в).

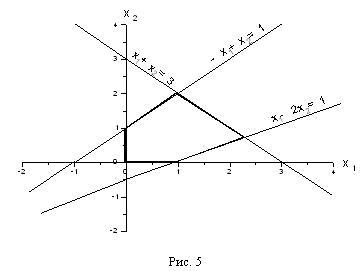
Сводя все вместе и добавляя условия х₁ ≥0,  х₂ ≥0  получим рисунок 5, где выделена область, в которой выполняются одновременно все ограничения (5). Обратите внимание на то, что получившаяся область имеет вид выпуклого многоугольника.

Вернемся теперь к общему случаю, когда одновременно выполняются неравенства:

(6)

Имеют место некоторые случаи, которые тут могут получится.

1. Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 6).

2. Неосновной случай - получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 7. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение х₁+ х₂≤ 3. Оставшаяся часть будет неограниченным выпуклым многоугольником.

3. Наконец, возможен случай, когда неравенства (6) противоречат друг другу, и допустимая область вообще пуста.

Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще целевая функция с₁ х₁+с₂ х₂→max .

Рассмотрим прямую с₁ х₁+с₂ х₂=L. При увеличении L прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором (с₁ ,с₂), так как это - вектор нормали к нашей прямой и одновременно вектор градиента функции f (х₁, х₂)=с₁ х₁+с₂ х₂.

А теперь сведем всё вместе. Итак, надо решить задачу:

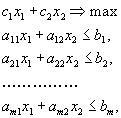
х₁ ≥0,  х₂ ≥0

Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая  с₁ х₁+с₂ х₂=L пересекает допустимую область. Это пересечение дает какие-то значения переменных (x₁ ,x₂), которые являются планами.

Увеличивая L, мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (рис. 9). В конце концов эта прямая выйдет награницу допустимой области - как правило, это будет одна из вершин многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение прямой с₁ х₁+с₂ х₂=L с допустимой областью будет пустым.

Поэтому то положение прямой с₁ х₁+с₂ х₂=L, при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.

Пример

Решить задачу:

(7)

Решение

Допустимая область изображена на рис. 5. Повторим еще раз этот рисунок, оставив только допустимую область и нарисовав дополнительно прямые с₁ х₁+с₂ х₂=L (рис. 10).

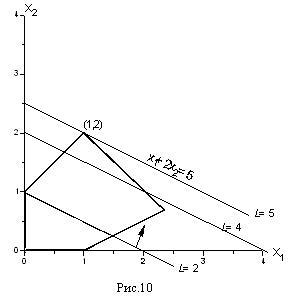
Пусть, например, L=2. Тогда прямая х₁+2х₂=2 проходит через точки (2,0) и (0,1) и изображена на рис. 10. Будем теперь увеличивать L. Тогда прямая начнёт двигаться параллельно самой себе в направлении, указанном стрелкой. Максимальное значение L получится тогда, когда прямая пройдет через вершину многоугольника, указанную на рисунке, и дальнейшее увеличение L приведет к тому, что прямая выйдет за пределы многоугольника и её пересечение с допустимой областью будет пустым.

Выделенная вершина лежит на пересечении прямых:

и поэтому имеет координаты х₁= 1, х₂= 2. Это и есть решение нашей задачи, т.е. х₁= 1, х₂= 2 есть оптимальный план задачи (7). При этом значение целевой функции L=1+2·2=5, что и дает её максимальное значение.

Следует обратить внимание на то, что оптимальный план, как правило, соответствует какой-то вершине многоугольника, изображающего допустимую область. И лишь в том случае, когда прямая с₁ х₁+с₂ х₂=L совпадает со стороной многоугольника (рис. 11), решение не будет единственным. Но и в этом случае вершины, соответствующие границам этой стороны, дают оптимальные планы нашей задачи линейного программирования. Таким образом, вершины допустимой области играют в решении задач линейного программирования особую роль.

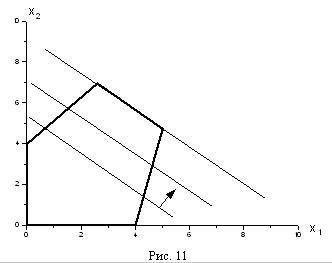
Если же допустимая область неограниченна, то и значение целевой функции может быть неограниченным.

Подводя итог этим примерам, можно сформулировать следующие положения:

1. допустимая область - это выпуклый многоугольник;

2. оптимум достигается в вершине допустимой области (если допустимая область ограничена и не пуста);

3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи.

 

8