3. Основы симплексного метода.

Решение основной задачи линейного программирования геометрическим методом является наглядным в случае двух и даже трех переменных. Для случая же большего числа переменных геометрический метод становится невозможным. Так называемый симплекс-метод принадлежит к числу аналитических методов решения основной задачи линейного программирования. Симплексный метод - это метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечно число шагов расчета либо найти оптимальное решение, либо установить, что оптимальное решение не существует.

Основное содержание метода состоит в следующем:

1. Указать способ нахождения начального опорного решения.

2. Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции ближе к оптимальному.

3. Задать критерии, которые позволяют своевременно прекратить перебор решений на оптимальном решении или сделать заключение об отсутствии решения.

Система ограничений в вычислительных методах обычно задается системой линейных уравнений

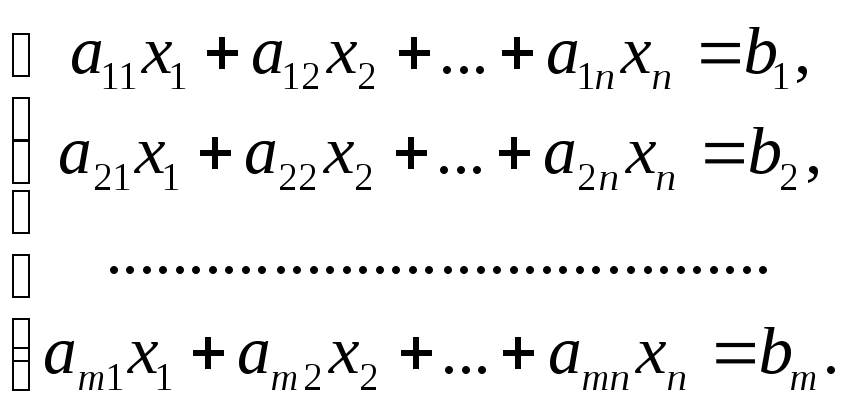(8)

и среди неотрицательных решений системы уравнений (8) надо найти такие, которые максимизировали бы линейную функцию .

Выразим через остальные переменные.

Замечание. Если ограничительные условия заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих). например, в неравенстве достаточно добавить к левой части некоторую величину и получится равенство .

Ограничительные условия могут задаваться и смешанным образом, т.е. неравенствами и уравнениями, тогда указанным путем их можно свести только к уравнениям.

Переменные (неизвестные) x₁, x₂,…, x_r называются базисными, а весь набор {x₁, x₂,…, x_r} – базисом, остальные переменные называются свободными. Подставляя в линейную форму L вместо базисных переменных их выражения через свободные, получим

.

Теперь полагая все свободные переменные равными нулю, найдем значения базисных переменных: , ,…,. Таким образом, решение системы является допустимым – оно называется базисным. Для полученного базисного решения значение линейной формы L_Б=γ₀. Решение задачи с помощью симплекс-метода распадается на ряд шагов, заключающихся в том, что от данного базиса Б переходим к другому базису с таким расчетом, чтобы значение L_Б уменьшалось или, по крайней мере, не увеличивалось, т.е. .

Идею метода проследим на конкретных примерах.

Пример.

Максимизировать линейную форму L= – x₄+x₅ при ограничениях: x₁+x₄–2x₅=1, x₂–2x₄+x₅=2, x₃+3x₄+x₅=3.

Решение. Данная система уравнений-ограничений совместна, так как ранги матрицы системы 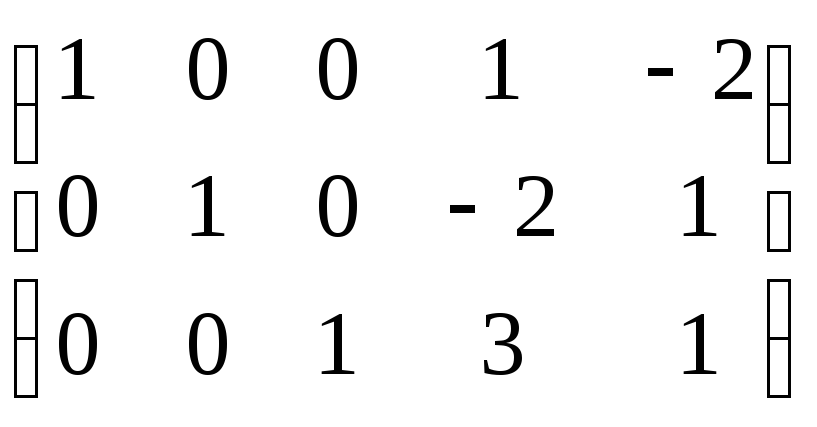и расширенной матрицы совпадают и равны 3. Следовательно, система уравнений совместна и три переменные (базисные) можно линейно выразить через две свободные переменные. Выразим, например x₁, x₂ и x₃ через x₄ и x₅, т.е. приведем систему к единичному базису:

(*)

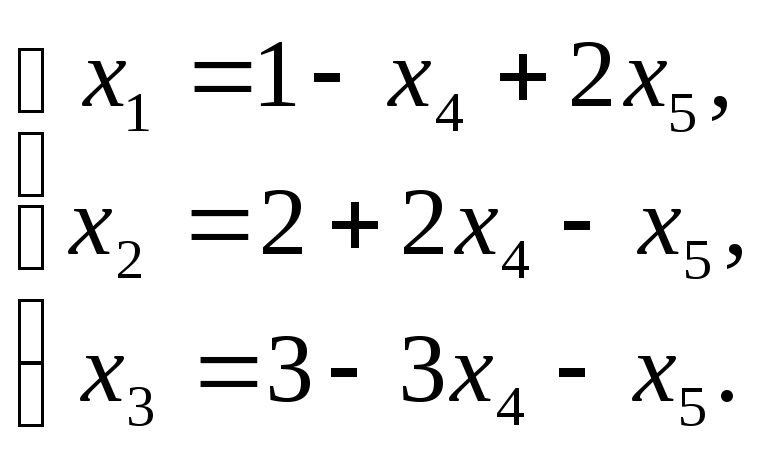Линейную форму L= – x₄+x₅ выразим через свободные переменные x₄ и x₅ (в данном примере L уже выражена через x₄ и x₅). Теперь, при x₄=0 и x₅=0, найдем значения базисных переменных: x₁=1, x₂=2, x₃=3, x₄=0, x₅=0 или (1,2,3,0,0). При найденном допустимом решении линейная форма L имеет значение 0, т.е. L₁=0.

Теперь попытаемся увеличить значение L₁; увеличение x₄ уменьшит L₁, так как перед x₄ стоит отрицательный коэффициент, а увеличение x₅ дает увеличение и L₁. Увеличим поэтому x₅ так, чтобы x₁, x₂ и x₃ не стали отрицательными, оставив x₄=0. Из второго уравнения системы (*) следует, что x₅ можно увеличить до 2. Таким образом, получаем следующие значения переменных: x₁=5, x₂=0, x₃=1, x₄=0, x₅=2 или (5,0,1,0,2).

Значение линейной формы L при этом допустимом решении равно L₂=2, т.е. при втором шаге оно увеличилось.

Далее, примем за свободные переменные x₂ и x₄, т.е. именно те переменные, которые в новом решении имеют нулевые значения. С этой целью из второго уравнения системы (*) выразим x₅ через x₂ и x₄ и получим

x₅=2–x₂+2 x₄. Тогда

(**)

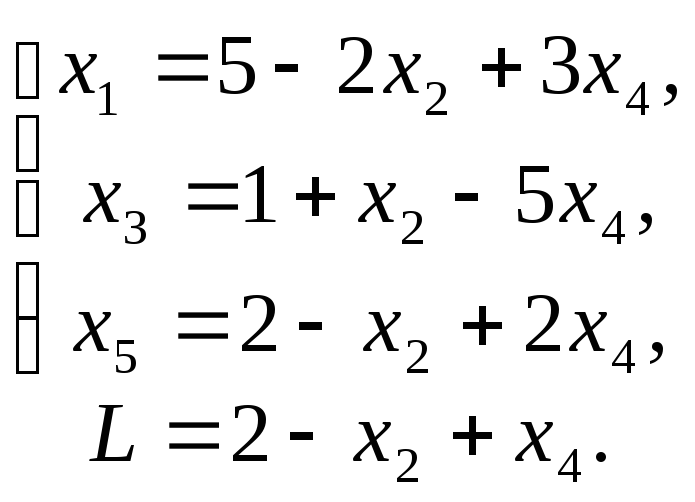Для увеличения значения L будем увеличивать x₄. Из второго уравнения системы (**) видно, что при условии неотрицательности x₃ значение x₄ можно довести до x₄=1/5. При этом условии новое допустимое решение есть x₁=28/5, x₂=0, x₃=0, x₄=1/5, x₅=12/5 или (28/5,0,0,1/5,12/5). Значение линейной формы при этом L₃=11/5.

Выразим теперь x₁, x₄, x₅ через свободные переменные x₂ и x₃:

(***)

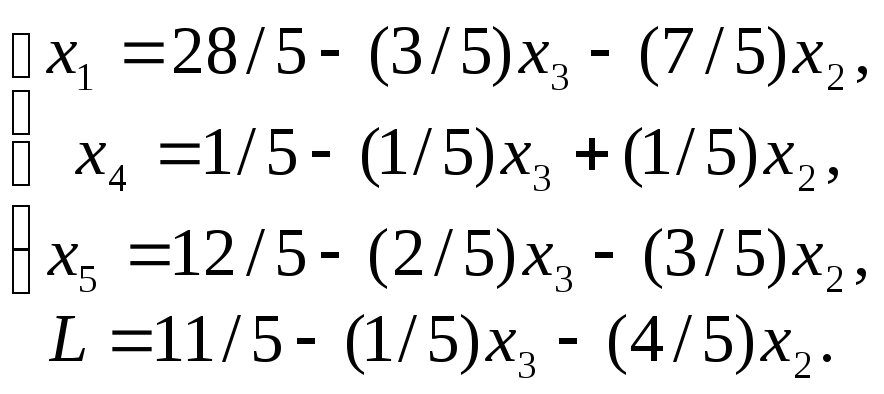Так как в последней линейной форме обе свободные переменные входят с отрицательными коэффициентами, то наибольшее значение L достигается при x₂=0 и x₃=0. Это означает, что решение (28/5,0,0,1/5,12/5) является оптимальным и L_max=11/5.

Однако наиболее простым способом решения данной задачи является использование симплекс-таблиц.