(2.5). Затем найти вероятность сдать тест как вероятность освоения всех 8 дидактических единиц. Ответ: ptest = p16 (6 −8 p + 3p2 )8 .

2.4.2.Смоделировать результат выполнения каждого задания двоичным кодом: 0, если задание не выполнено; 1, если задание выполнено правильно. Организовать подсчёт правильно выполненных заданий в каждой дидактической единице и определение результата теста в целом. По серии испытаний оценить вероятность сдачи теста при заданном p .

2.4.3.Смоделировать результат прохождения каждой дидактической единицы как случайную величину, имеющую биномиальное распределение

P(X = k) = C4k pk (1− p)4−k , k = 0, 1, 2, 3, 4.

Определить результат теста в целом. По серии испытаний оценить вероятность сдачи теста при заданном p .

Сравнить результаты, получаемые всеми описанными способами.

Контрольные вопросы

1.Что такое сумма событий, произведение событий, несовместные события, полная группа событий, противоположные события?

2.Запишите формулу для суммы двух событий, сформулируйте следствия из неё.

3.Что такое зависимые и независимые события?

4.Как вычисляется вероятность произведения событий?

5.Запишите и объясните смысл формулы полной вероятности.

6.Приведите примеры дискретных случайных величин.

7.Какая задача приводит к формуле Бернулли и биномиальному закону распределе-

ния?

8.Виды единичного жребия в методе Монте-Карло.

9.Проанализируйте результаты решения задания 2.4. Постройте график зависимости вероятности успешного прохождения всего теста данным студентом от вероятности правильного выполнения им тестовых заданий.

Работа 3

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ХАРАКТЕРИСТИК СИСТЕМЫ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Оценивание числовых характеристик случайных величин, параметров функций регрессии и коэффициента корреляции

Время на выполнение и защиту – 2 часа

Цель работы:

1)рассмотрение характеристик систем дискретных случайных величин;

2)углублённое изучение понятий «корреляция» и «регрессия» на основе проведения численных экспериментов;

38

3) изучение ряда функций Excel и Mathcad.

Система дискретных случайных величин

Если результат опыта описывается не одной, а несколькими случайными величинами, то говорят о системе случайных величин. Иллюстрируем основные положения теории систем дискретных случайных величин нижеследующим примером.

Пример 11. Генератор случайных чисел выдаёт два целых числа, каждое из которых с одинаковой вероятностью может являться нулём, единицей, двойкой или тройкой. Случайная величина X – суммарное количество двоек и троек среди двух генерированных чисел, случайная величина Y – сумма генерированных чисел. Исследовать характер связи между случайными величинами X и Y.

Нетрудно составить табл. 3.1.

Табл. 3.1. Исходная информация о поведении системы случайных величин (пример 11)

Возможные комбинации		Вероятности комбинаций	X	Y
генерированных чисел
0	0	1 16	0	0
0	1	2 16	0	1
0	2	2 16	1	2
0	3	2 16	1	3
1	1	1 16	0	2
1	2	2 16	1	3
1	3	2 16	1	4
2	2	1 16	2	4
2	3	2 16	2	5
3	3	1 16	2	6

Очевидно, что с ростом значений X случайная величина Y имеет тенденцию к увеличению, но записать эту связь с помощью некоторой однозначной функции y = f (x) нельзя: например, при X = 2 возможны три различных значения Y (4,

5, 6), причём с разными вероятностями. Такого рода нефункциональные зависи-

мости называются вероятностными или корреляционными. Отобразим закон распределения системы случайных величин (X, Y) с помощью табл. 3.2:

39

Табл. 3.2. Закон распределения системы дискретных случайных величин (пример 11)

yi		xi		p(yi )
	0	1	2
0	1/16	0	0	1/16
1	1/8	0	0	1/8
2	1/16	1/8	0	3/16
3	0	1/4	0	1/4
4	0	1/8	1/16	3/16
5	0	0	1/8	1/8
6	0	0	1/16	1/16
p(xi )	1/4	1/2	1/4	∑p =1

Во внутренние клетки таблицы помещены вероятности определённых состояний системы: pij = p(xi , y j ). Заметим, что вероятность состояния (1, 3) склады-

вается из вероятностей двух различных исходов (см. табл. 3.1). Законы распре-

деления каждой составляющей (X или Y) могут быть получены как

P(X = xi ) = ∑ pij ,	P(Y = y j ) = ∑ pij .
j	i

Найденные по этим формулам вероятности указаны в нижней строке и правом столбце таблицы. Определяя вероятность состояния системы как вероятность произведения событий

pij = P(X = xi )P(Y = y j X = xi ) = P(Y = y j )P(X = xi Y = y j ),

получаем условные законы распределения составляющих:

P(X = xi Y = y j ) = pij / P(Y = y j ),

(3.1)

P(Y = y j X = xi ) =pij / P(X = xi ).

Найдём, например, закон распределения Y при условии, что X = 1. Поскольку P(X =1) =1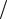2, получаем:

P(Y = 2 X =1) = 18 : 12 = 14,

P(Y =3 X =1) = 14 : 12 = 12,

P(Y = 4 X =1) = 18 : 12 = 14.

Математическим ожиданием дискретной случайной величины X назы-

вается характеристика

40

M (X ) = ∑xi P(X = xi ) ,	(3.2)
i

(суммирование идёт по всем возможным значениям X ), имеющая смысл среднего арифметического наблюдаемых значений X , когда эти значения распределены в точном соответствии с законом распределения вероятностей.

Аналогично

M (Y ) = ∑y j P(Y = y j ) .	(3.3)
j

Статистической оценкой математического ожидания служит выборочная средняя – среднее значение случайной величины, вычисленное по всем наблюдавшимся значениям.

Условное математическое ожидание – это математическое ожидание одной случайной величины (Y) при условии, что другая случайная величина (X) принимает определённое значение xi :

M (Y		X = xi ) = ∑y j P(Y = y j		X = xi )	(3.4)
		j

Если M (Y X = x) =ϕ(x) , то ϕ(x) называется функцией регрессии Y на

(по) X. Функция регрессии устанавливает форму корреляционно-регрессионной связи двух случайных величин. Если

ϕ(x) = ax +b ,

(3.5)

то говорят о линейной корреляции.

Продолжая пример 11, найдём условные математические ожидания и функцию регрессии Y по X. Воспользовавшись полученными выше значениями условных вероятностей P(Y = y j X =1) , получаем

M (Y X =1) = 2 14 + 3 12 + 4 14 = 3.

Таким же образом можно найти математические ожидания Y при других значениях X. Более простой способ позволяет сразу вывести общую формулу для M (Y X = x) =ϕ(x) . Вспомним, что x – это число двоек и троек, а (2 – x) – число

единиц и нулей среди двух генерированных цифр. Отсюда

M (Y X = x) = 2,5x + 0,5(2 − x) = 2x +1.

Итак, ϕ(x) = 2x +1, (имеет место линейная корреляция случайных величин),

M (Y X = 0) =1, M (Y X =1) = 3, M (Y X = 2) = 5.

Дисперсией дискретной случайной величины X называется характеристика степени рассеивания (разброса) значений X :

41

D(X ) =σ 2 (X ) = M [X − M (X )]2 = ∑[xi − M (X )]2 pi .	(3.6)
i

Квадратный корень из дисперсии называется среднеквадратическим отклоне-

нием σ(X ) .

Статистической оценкой дисперсии случайной величины служит выборочная дисперсия:

	D =σx2 =		− (		)2 ,
		x2				(3.7)
				x

где x и x2 – выборочные средние, вычисленные по наблюдавшимся значениям

случайных величин X и X 2 соответственно. Вопрос о «качестве» оценок x и D будет обсуждаться позже (работа 7).

Корреляционным моментом (ковариацией) случайных величин X и Y на-

зывается математическое ожидание произведения их отклонений:
µ(X ,Y ) = M{[X − M (X )][Y − M (Y )]}= M (XY) −M (X )M (Y ) .	(3.8)

Корреляционный момент двух независимых случайных величин равен нулю. Если µ(X ,Y ) ≠ 0 , то случайные величины называются коррелированными. Кор-

релированные величины зависимы.

Коэффициентом линейной корреляции случайных величин X и Y назы-

вается безразмерная характеристика

	r(X ,Y ) =	µ(X ,Y )	.	(3.9)
		σ(X )σ(Y )

Статистическая оценка коэффициента корреляции (выборочный коэффициент корреляции) строится по следующему принципу: величины, входящие в формулу (3.9), заменяются их статистическими аналогами:

r =

xy

−

x

y

.

(3.10)

xy	σxσy

Если между двумя случайными величинами существует линейная зависимость (её можно рассматривать как предельно тесную корреляцию!), то модуль коэффициента корреляции (3.9) равен единице.

Коэффициент корреляции и угловой коэффициент функции линейной регрессии a (3.5) имеют одинаковый знак. Этот знак отражает характер связи: если с ростом X величина Y в среднем возрастает, то знак положительный, если убывает – то отрицательный.

Область значений коэффициента корреляции: r(X ,Y ) ≤1.

Закончим рассмотрение примера 11. Можно вычислить: 42

M (X ) =1; σ(X ) =	1	; M (Y ) = 3; σ(Y ) =	5	2	;
	2

M (XY ) = 2 18 +3 14 + 4 18 +8 116 +10 18 +12 116 = 4;

r(X , Y ) = (4 − 3 1) 2	≈ 0,894.
5

Задание для лабораторной работы

Задание 3.1. Методом Монте-Карло оценить коэффициенты функции регрессии Y по X и коэффициент корреляции между X и Y для величин, фигурирующих в примере 11.

Смысл настоящей работы состоит в том, чтобы, моделируя систему случайных величин с помощью генератора случайных чисел, получить (на основе случайных выборок объёма 10000) статистические оценки характеристик этой системы и убедиться в том, что они (оценки) достаточно близки к истинным значениям оцениваемых характеристик.

Инструкция по выполнению задания в Excel

Моделирование работы генератора двух случайных чисел может быть реализовано аналогично тому, как в задании 1.1 моделировалось бросание двух игральных костей. Отличие состоит лишь в том, что на этот раз мы имеем не шестигранную, а «четырёхгранную игральную кость», на которой с равной вероятностью выпадают числа 0, 1, 2 и 3. Таким образом, надо воспользоваться формулой =ОТБР(4*СЛЧИС()).

Значение X (число двоек и троек) можно вычислить с помощью формулы

=СЧЁТЕСЛИ(диапазон;2)+СЧЁТЕСЛИ(диапазон;3),

где под диапазоном имеются в виду адреса ячеек с двумя генерированными в данном испытании числами. Вычисление Y легко организовать с помощью функции СУММ(диапазон). Подчеркнём, что значения X и Y определяются по

двум числам, генерированным в данном испытании. Поэтому диапазон будет включать в себя всего лишь 2 ячейки.

С помощью автозаполнения «растянем» таблицу до 10000-го номера испытания.

В последней строке таблицы поместим средние значения величин с помощью функции СРЗНАЧ (диапазон) из списка статистических функций. Для этого достаточно ввести эту функцию только в ячейку столбца B и с помощью автозаполнения «растянуть» вправо. Легко догадаться, что среднее значение генерированного числа окажется близким к 1,5, среднее значение X – близким к 1, среднее значение Y – близким к 3. Убедитесь, что средние значения X и Y близки к математическим ожиданиям M (X ) и M (Y ), приведённым выше.

43

Угловой коэффициент a функции линейной регрессии Y по X

M (Y X = x) = ax +b

оценивается с помощью функции НАКЛОН (диапазон значений Y; диапазон значений X) из статистических функций.

Свободный член b функции линейной регрессии можно оценить, как

b* = y − a* x ,

где звёздочка обозначает оценку.

Коэффициент корреляции оценивается с помощью функции КОРРЕЛ (массив 1; массив 2) из списка статистических функций. В качестве аргумен- тов-массивов нужно задать диапазоны с ячейками, содержащими значения X и Y (в отличие от функции НАКЛОН здесь порядок аргументов не важен).

Можно рассчитать коэффициент корреляции и без функции КОРРЕЛ, непосредственно по формуле (3.10). Для этого придётся:

1.ввести в таблице дополнительный столбец для произведений X на Y и рассчитать среднюю выборочную xy ;

2.рассчитать среднеквадратические отклонения σx и σ y с помощью

функции СТАНДОТКЛОНП(диапазон).

Полученные оценки коэффициентов регрессии и корреляции сравните с полученными при решении примера 11 их точными значениями.

Инструкция по выполнению задания в Mathcad

Моделирование работы генератора двух случайных чисел может быть реализовано аналогично тому, как в задании 1.1 моделировалось бросание двух игральных костей. Однако на этот раз с равной вероятностью выпадают целые числа не от 1 до 6, а от 0 до 3. Поэтому мы будем использовать две встроенные в Mathcad функции: rnd(х) и floor(z). С функцией rnd(х) мы уже неоднократно встречались и знаем, что она генерирует случайное число, равномерно распределенное на интервале (0, х). Функция floor(z) возвращает наибольшее целое, меньшее или равное z, и относится к категории Truncation and Round-Off (Отбрасывание и округление). Комбинация этих функций вида floor(rnd(4)) даст нам искомое случайное целое число от 0 до 3. (Если же вы хотите воспользоваться уже известной вам по работе 1 функцией ceil, то вам придётся сконструировать чуть более сложную комбинацию ceil(rnd(4)-1). Почему?)

В данной работе нам понадобится вычислить и запомнить векторы x и y, имеющие по n = 10000 элементов. Для их вычисления создадим подпрограммуфункцию f(n), в которой будем n раз генерировать по 2 случайных числа. Суммы этих двух чисел будут элементами вектора y. Элементам вектора x будем присваивать значение равное 2, если оба случайных числа больше 1 (т.е. равны 2 или 3), значение равное 0, если оба числа меньше 2, и значение 1 во всех других случаях. Поскольку результатом работы подпрограммы-функции может

44

быть только одна величина (число, вектор или матрица) то объединим эти векторы в матрицу, имеющую n строк и 2 столбца. После завершения описания подпрограммы присвоим значение функции f(10000) некоторой матрице s. Затем, используя дискретные аргументы, создадим векторы x и y, присвоив им значения соответственно первой и второй строк матрицы s .

Средние значения величин вычислим с помощью встроенной функции mean(A, B, C, ...), которая возвращает арифметическое среднее (среднее значение) элементов A, B, C, ..... Найти эту функцию можно в категории Statistics (Статистика). Поскольку нам нужно вычислять среднее значения из элементов одного вектора, то запишем хс:= mean(х), а оставшиеся пустые местозаполнители просто удалим.

Легко догадаться, что среднее значение х окажется близким к 1, а среднее значение у – близким к 3. Убедитесь, что средние значения х и у близки к математическим ожиданиям M (X ) и M (Y ), приведённым выше.

Коэффициенты функции линейной регрессии

M (Y X = x) = a + bx

оцениваются с помощью функции line(x,y) из категории Curve fitting and smoothing (Аппроксимация и сглаживание кривой). Данная функция возвращает вектор, содержащий коэффициенты уравнения прямой вида y = ax +b , наи-

лучшим образом аппроксимирующей данные в векторах х и у.

Коэффициент корреляции оценивается с помощью функции corr(x,y) из категории Statistics (Статистика). Данная функция возвращает коэффициент корреляции элементов из х и у. В отличие от функции line(x, y) здесь порядок аргументов не важен.

Фрагмент рабочего документа Mathcad, содержащий перечисленные вычисления приведен ниже

f(n) := for k 1.. n

a← floor (rnd (4))

b← floor (rnd (4)) zk,2 ← a + b

zk,1 ← 2 if a > 1 b > 1 zk,1 ← 0 if a < 2 b < 2 zk,1 ← 1 otherwise

z

s:= f(10000) i := 1.. 10000

xi := si,1

yi := si,2

xc := mean(x) yc := mean(y)

reg := line(x,y)

kor := corr(x,y)

45