§4. Обратная матрица

Понятие обратной матрицы вводится лишь для квадратной матрицы. Если А – квадратная матрица порядка n, то обратной для нее называется

матрица А, удовлетворяющая условию

(1)

где Е – единичная матрица порядка n.

Можно доказать, что (1)

Опр. Если , то матрица называетсяневырожденной, если , товырожденной.

Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т.е. .

Без доказательства.

Правило нахождения обратной матрицы.

Дана квадратная невырожденная матрица

1)Найти определитель матрицы А

2)Найти алгебраические дополнения Авсех элементов определителя матрицыА, составить из них матрицу и транспонировать ее

3)Умножить эту матрицу на , в итоге получим обратную матрицу

Пример 4.1

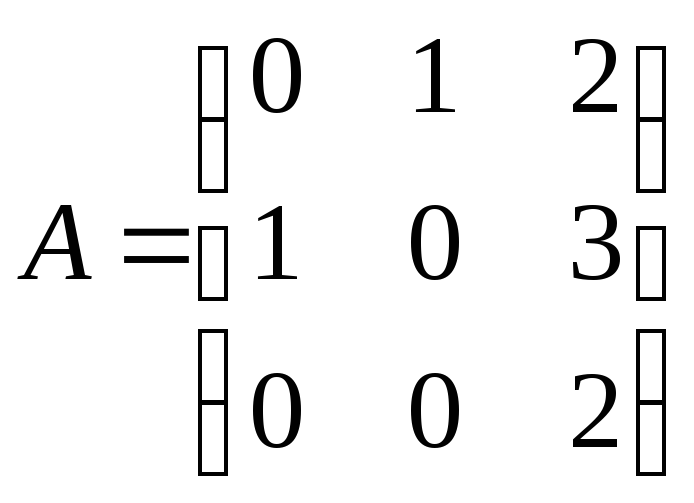; Найти .

Решение: 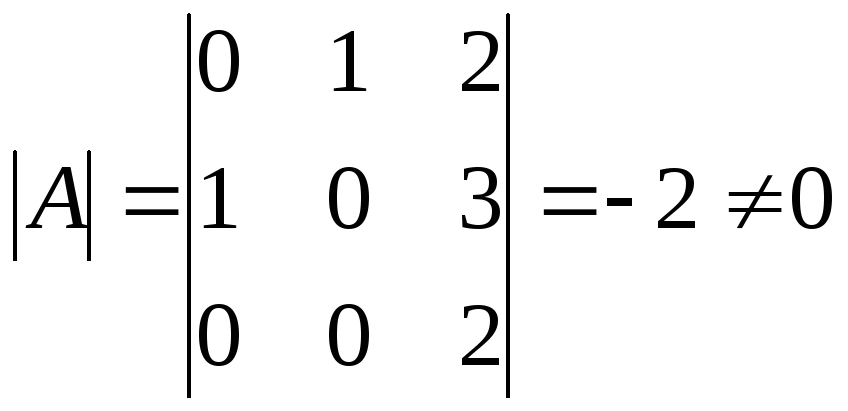, значит существует обратная матрицаA^-1.

где – алгебраическое дополнение,

– минор.

.

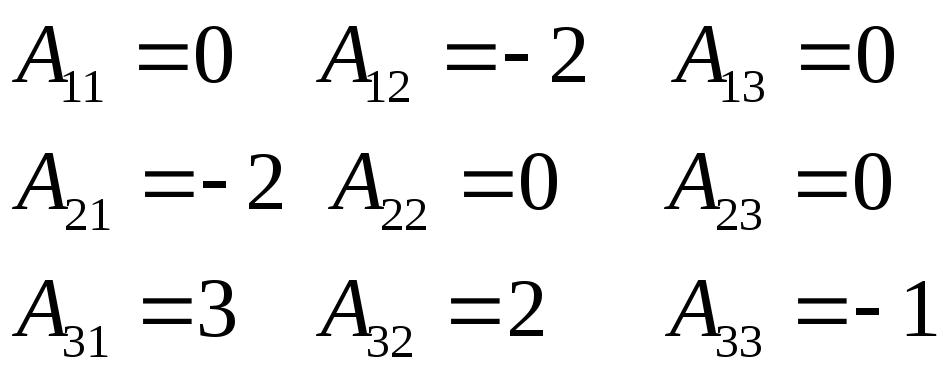
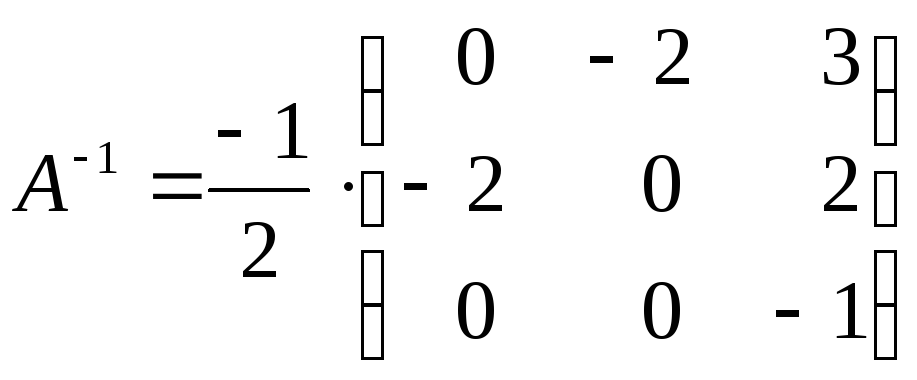Проверка:

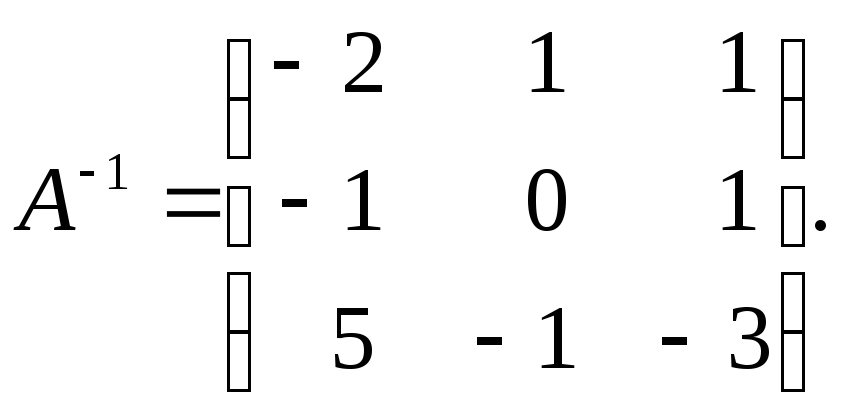
Пример 4.2 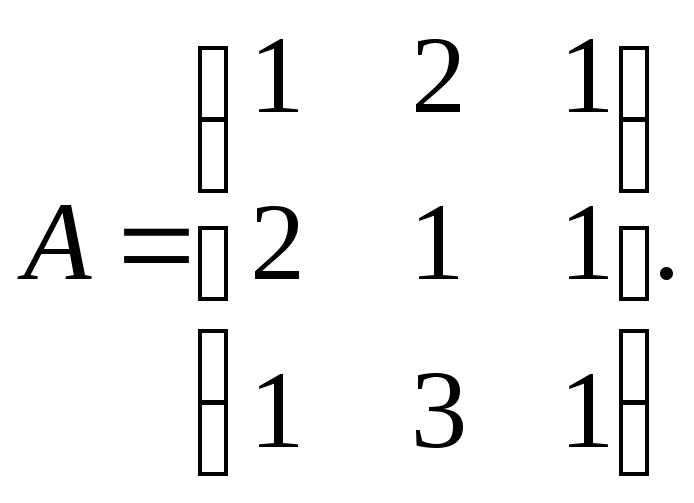НайтиA^-1. Ответ:

§5. Ранг матрицы.

I. Определение ранга матрицы

Рассмотрим прямоугольную матрицу

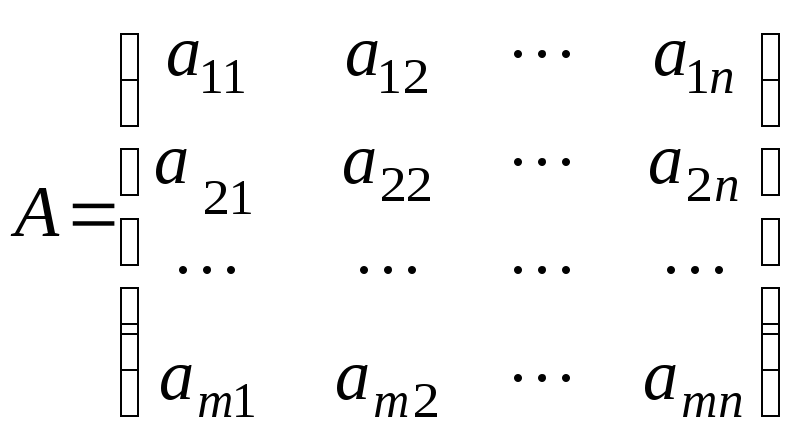
Выделим из этой матрицы произвольные k строк и k столбцов. Получим квадратную матрицу k–го порядка.

Опр. Минором k–го порядка матрицы А называется определитель квадратной матрицы, получающийся из матрицы А выделением произвольных k строк и k столбцов. Обозначается

Замечание. Матрица имеетминоровk -го порядка.

Опр. Рангом матрицы А называется наивысший из порядков отличных от нуля миноров матрицы А. Обозначается r (A); rang A; rg A.

Итак, ранг матрицы А равен r, т.е r(A)=r, означает, что в матрице А есть минор порядка r, отличный от нуля, а всякий минор порядка больше r, равен нулю

.

II. Элементарные преобразования. Эквивалентные матрицы.

Элементарными преобразованиями матрицы называется

1. перестановка строк (столбцов) матрицы; транспонирование матрицы.

2. умножение строки (столбца) на число k0.

3. прибавление к элементам одной строки (столбца) элементов другой строки (столбца), умноженных на одно и тоже число.

4. Отбрасывание нулевых строк (столбцов).

Матрицы, получающиеся одна из другой при помощи элементарных преобразований, называются эквивалентными: А ~ С.

Можно доказать, что элементарные преобразования матрицы не меняют ее ранга:

Если A~C, то r(A) = r(C).

Данный вывод используется при вычислении ранга матрицы. Данная матрица А преобразуется в эквивалентную матрицуступенчатого вида:

, где С,,

Можно доказать, что r(С) = r r(А) = r.

Пример 5.1 Найти r(A) с помощью элементарных преобразований

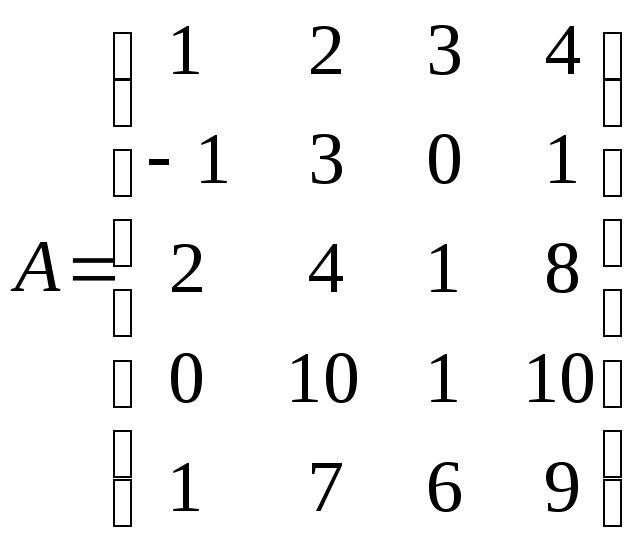
III. Базисный минор.

Пусть ранг матрицы А равен r: r(A)=r. Всякий отличный от нуля минор порядка r называется базисным. Строки и столбцы выбранного базисного минора называются базисными. Матрица может иметь несколько базисных миноров.

§6. Системы m линейных уравнений с n неизвестными.

Рассмотрим систему m линейных уравнений с n неизвестными.

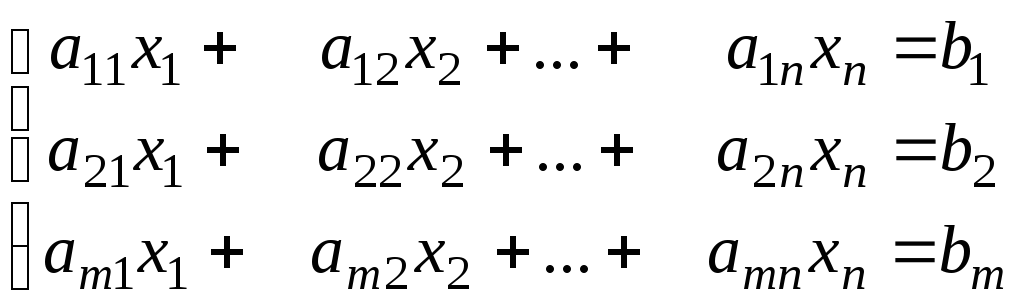(1)

A= 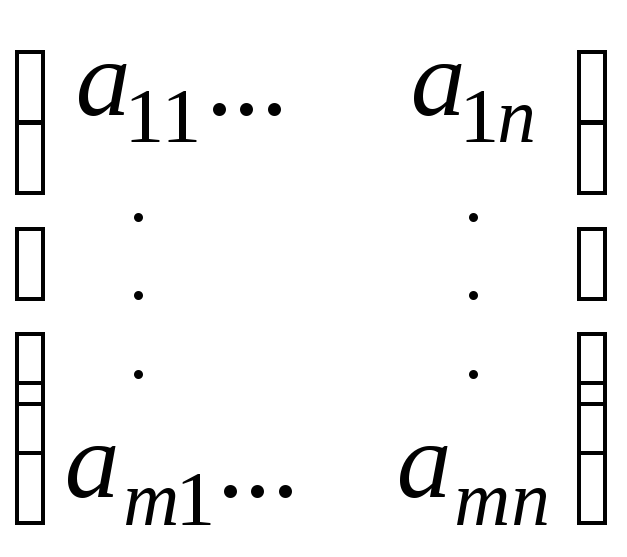– матрица системы, X=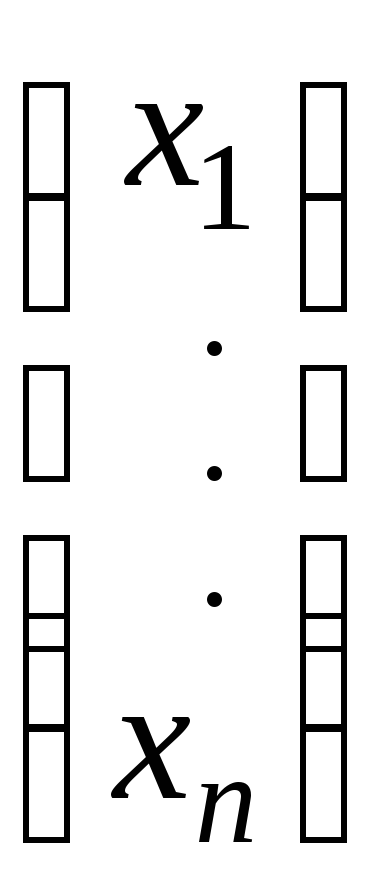 – матрица-столбец неизвестных, B= 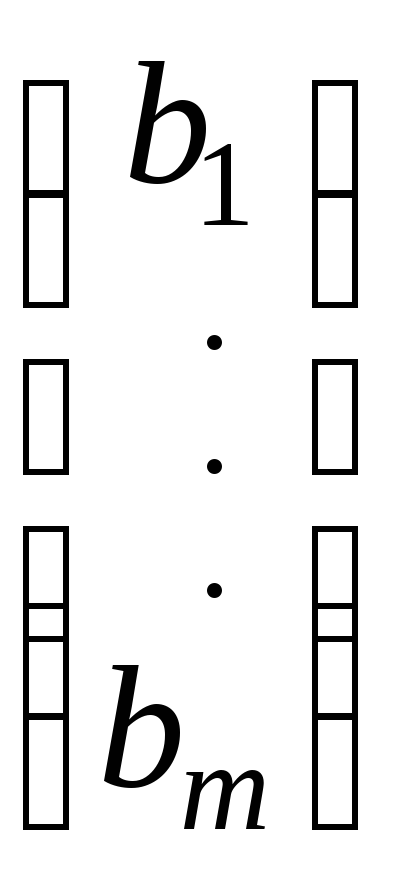– матрица-столбец свободных членов.

() – запись системы в матричном виде.

Если , то система называетсяоднородной.

Если , то система называетсянеоднородной.

Опр. Решением системы называется всякая совокупность n чисел х_1…, х_n, которая будучи подставлена в систему, превращает каждое ее уравнение в тождество.

Система уравнений, имеющая хотя бы одно решение называется совместной. Если решение единственное, то система называется определенной, если более одного решения, то неопределенной.

Система уравнений, не имеющая решений, называется несовместной.

Рассмотрим матрицу из коэффициентов при неизвестных

А = 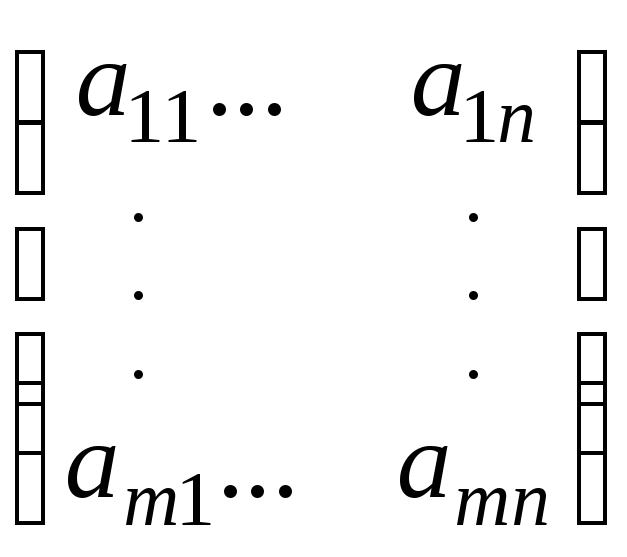–матрица системы

Дополним ее столбцом свободных членов

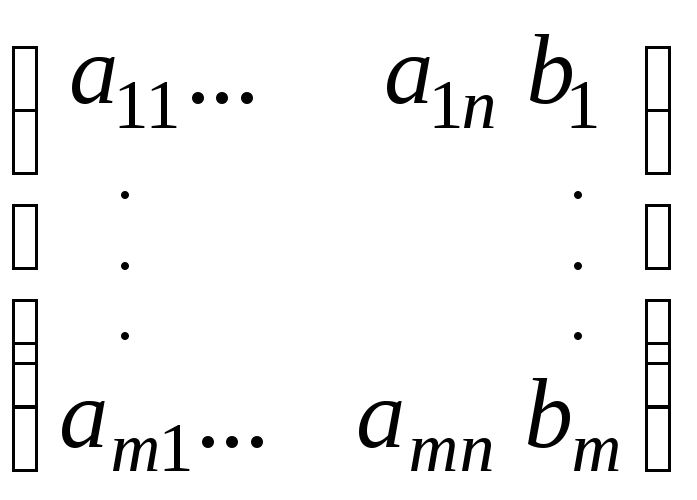= –расширенная матрица.

Теорема Кронекера-Капелли.

(Л.Кронекер 1823-1891г. Немецкий математик.

А.Капелли 1855-1910г. Итальянский математик).

Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы этой системы.

Система совместна r (A) = r(). Без доказательства.

Следствие. Если r(A) система несовместна.

r(A)=r – ранг матрицы системы

r() – ранг расширенной матрицы

n – число неизвестных

r(A) = r() =r r(A)

система совместна система несовместна,

нет решений

r=n

единственное бесконечное

решение множество

решений

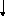
r – базисн. неизв.

(n-r) – своб. неизв.

Пример 6.1

Исследовать систему уравнений. В случае совместности решить

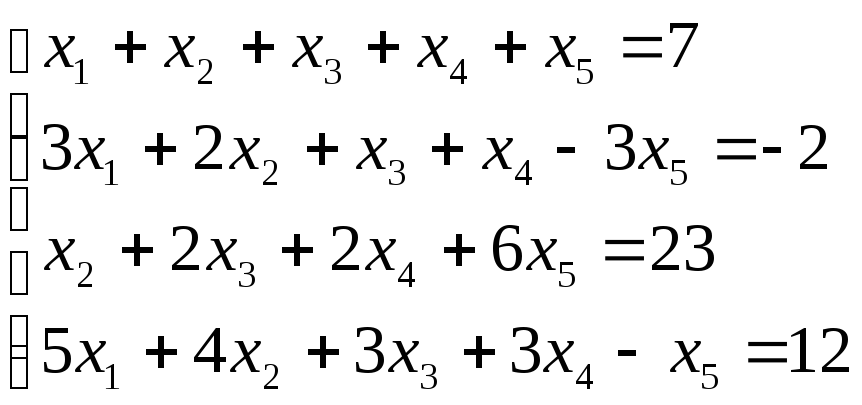
Ответ: Система совместна и имеет бесконечное множество решений вида:

, ,где

Пример 6.2

Исследовать систему

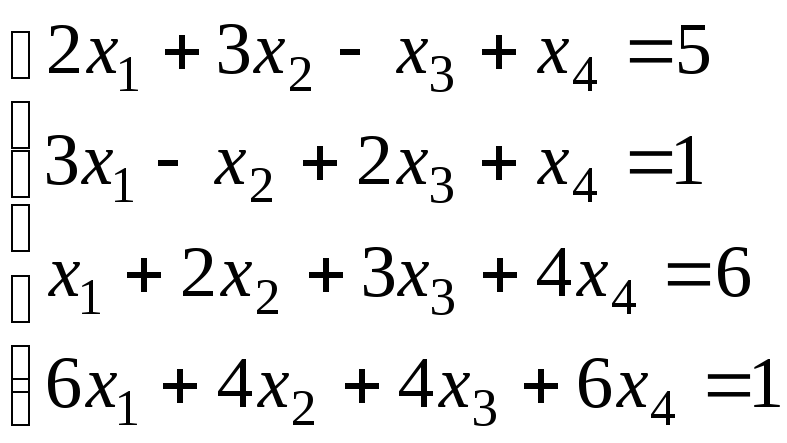
Ответ: Система несовместна (нет решений)

Пример 6.3

Исследовать и решить систему уравнений.

Ответ: Система совместна и имеет единственное решение ,,