Свойства отношения выводимости
Свойства отношения выводимости
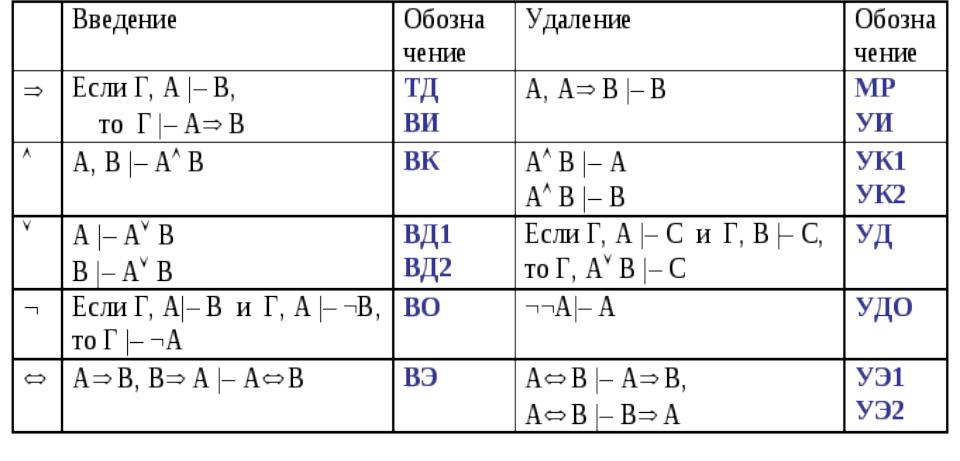
Некоторые вспомогательные правила вывода
Проблема разрешимости
Проблема разрешимости исчисления выказываний заключена в доказательстве существования алгоритма, который позволил бы для любой формулы исчисления высказываний определить ее доказуемость. Любая формула исчисления высказываний может быть представлена формулой алгебры высказываний. Эффективность процедуры разрешения показана таблицами истинности для различных наборов значений пропозициональных переменных.
Определение. Формальная аксиоматическая теория называется разрешимой, если существует алгоритм, позволяющий за конечное число шагов относительно любой формулы языка этой теории установить, доказуема ли эта формула или нет.
Следствие из МТ4 и МТ6. Теория L разрешима.
Проблема непротиворечивости
Проблема непротиворечивости исчисления высказываний заключена в доказательстве невыводимости формулы и ее отрицания.
Следствие из МТ 4. Теория L непротиворечива.
Исчисление высказываний непротиворечиво, т. к. каждая формула, доказуемая в исчислении высказываний, является тождественно истинной формулой в алгебре высказываний и легко проверяется на таблицах истинности.
Тогда отрицание формулы не является тождественно истинной формулой, что проверяется на таблицах истинности и при доказательстве в исчислении высказываний ведет к противоречию.
Некоторые теоремы и правила, используемые в исчислении высказываний
1.Ф, А├ В Ф├ А → В – теорема дедукции.
2.А├ В ├ А → В – следствие из теоремы дедукции (при Ф = Ø, где Ф – список формул, А и В – отдельные формулы).
Правило подстановки. Если Е – выводимая формула, содержащая символ
А(т.е. Е(А)), то выводима формула Е(В), полученная из Е заменой всехE(A)вхождений.
Ана произвольную формулуE(В:B)т.е.
Правило modus ponens (mp). Если набор формул А, В, С является частным случаем набора формул А, А → В, то формула С является непосредственно выводимой из формул А и В.
Правило - Общие свойства символа ╟ - непосредственная выводимость (├ - выводимость).
• При n > 1 А1, А2, …, Аn ╟ А1; А1, А2, …, Аn ╟ А2; …, А1, А2, …, Аn ╟ Аn – из набора формул непосредственно выводима каждая.
•Если А1, А2, …, Аn ╟ С, то
А1, А2, …, Аn, В1, …, Вm ╟ С, т.е. добавление лишних формул при сохранении
непротиворечивости не влияет на выводимость.
Те же свойства справедливы для выводимости ├.
Правило введения отрицания.
(Г , А├ В и Г , А├ В) (Г А)
Существуют и другие аксиоматизации исчисления высказываний.
Аксиоматизация исчисления высказываний
Гильберт, Аккерман (1938)
А: Основные: , ¬; |
def |
|
||
дополнительные: |
(А В |
A |
|
B) |
Р: А А А А А В
А В В А (В С) (А В А С)
R: modus ponens
Клини (1952)
А: ¬, Λ, , →
Р: А (В А)
( А (В С)) (( А В) ( А С))
A B A
A B B
A (B A B) A ( A B)
B ( A B)
( A C) ((B C) (( A B) C)) ( A B) (( A B) A)
def
A ( A) A
R: modus ponens